Seite 3: Unterschied zwischen den Versionen
Aus DMUW-Wiki
| Zeile 39: | Zeile 39: | ||
<div style="border: 2px solid #00c5cd; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid #00c5cd; background-color:#ffffff; padding:7px;"> | ||
<big>'''Aufgabe 1:'''</big><br> | <big>'''Aufgabe 1:'''</big><br> | ||
| − | |||
| − | + | <div class="multiplechoice-quiz"> | |
| − | < | + | |
| − | + | <math> \frac{2}{8} </math> * <math> \frac{2}{8} </math> = (<math> \frac{2}{32} </math>) (<math> \frac{4}{32} </math>) (!<math> \frac{1}{8} </math>) | |
| − | + | ||
| − | < | + | <math> \frac{3}{7} </math> * <math> \frac{4}{3} </math> = (<math> \frac{12}{21} </math>) (<math> \frac{4}{7} </math>) (!<math> \frac{28}{9} </math>) |
| − | < | + | |
| − | + | <math> \frac{2}{4} </math> * <math> \frac{4}{3} </math> = (!<math> \frac{4}{6} </math>) (!<math> \frac{8}{4} </math>) (!<math> \frac{6}{16} </math>) | |
| − | < | + | |
| − | < | + | |
| − | + | ||
</div> | </div> | ||
| − | + | ||
| − | + | ||
| + | |||
| + | |||
| + | |||
| + | |||
'''→[[Benutzer:Sandra Hemrich/Repräsentationsform: ikonisch/Seite 4|Hier geht`s zur 4. Seite]]''' | '''→[[Benutzer:Sandra Hemrich/Repräsentationsform: ikonisch/Seite 4|Hier geht`s zur 4. Seite]]''' | ||
Version vom 19. Dezember 2009, 16:28 Uhr
2.Station: Multiplikation zweier Brüche
Hast du nun anhand der Zeichnung die Regel der Multiplikation eines Bruches mit einer ganzen Zahl erkannt??????
Kreuze an!!! Welche Rechenregel stimmt? (!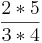 ) (
) (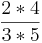 ) (
) (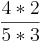 )
)
</div>
30px Merke
Multiplikation zweier Brüche
|
- allgemein:
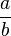 *
* 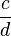 =
= 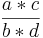
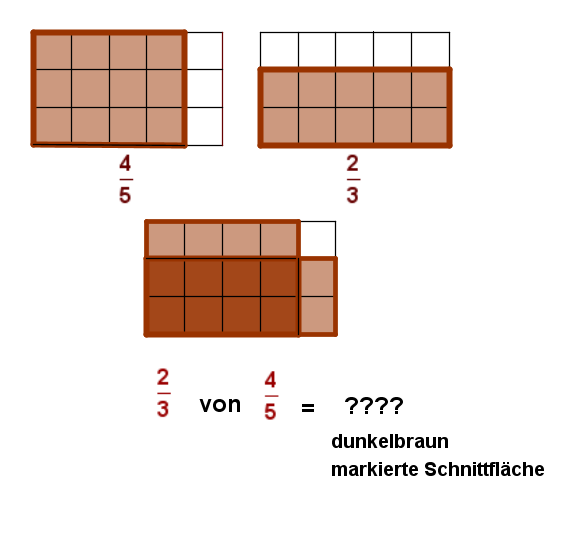
- Beispiel oben:
 *
*  =
= 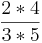
- Es gilt auch das Kommutativgesetz!!!
Die folgenden Aufgaben sollen dir zeigen, ob du die Regel verstanden hast und es anwenden kannst:
 *
* 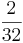 ) (
) (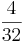 ) (!
) (! )
)
 *
*  = (
= (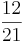 ) (
) ( ) (!
) (!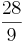 )
)
 *
*  ) (!
) (!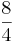 ) (!
) (!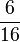 )
)

