Kongruenzabbildungen/Drehung/Seite 2b: Unterschied zwischen den Versionen
| Zeile 44: | Zeile 44: | ||
Verwende als Hilfe das Applet und die eben berechneten Vektoren.} | Verwende als Hilfe das Applet und die eben berechneten Vektoren.} | ||
| − | + Die Strecken | + | + Die Strecken [ZP] und [ZP'] stehen senkrecht aufeinander |
| − | + Man erhält die Koordinaten des Bildvektors <math>\overrightarrow { ZP' }</math> durch vertauschen der Koordinaten des Urvektors < | + | + Man erhält die Koordinaten des Bildvektors <math>\overrightarrow { ZP' }</math> durch vertauschen der Koordinaten des Urvektors <math>\overrightarrow { ZP }</math> |
- Die y-Koordinate des Bildvektors <math>\overrightarrow { ZP' }</math> bekommt das umgekehrte Vorzeichen | - Die y-Koordinate des Bildvektors <math>\overrightarrow { ZP' }</math> bekommt das umgekehrte Vorzeichen | ||
| Zeile 60: | Zeile 60: | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
| − | 1. Gib zuerst die Koordinaten des Verbindungsvektor < | + | 1. Gib zuerst die Koordinaten des Verbindungsvektor <math>\overrightarrow { ZC }</math> an, wenn der Punkt C(2|14) um den Punkt Z(1|1) um 90° gedreht wird! <br/> |
{| | {| | ||
|- | |- | ||
| Zeile 72: | Zeile 72: | ||
|| [[Bild:klammer2MM.gif]] | || [[Bild:klammer2MM.gif]] | ||
|} | |} | ||
| − | Nach dem was du gerade gelernt hast ist es jetzt ganz einfach, die Koordinaten des Vektors < | + | Nach dem was du gerade gelernt hast ist es jetzt ganz einfach, die Koordinaten des Vektors <math>\overrightarrow { ZC' }</math> zu berechnen!<br/> |
{| | {| | ||
|- | |- | ||
Version vom 7. Januar 2010, 16:19 Uhr
Teilaufgabe c)
Schauen wir uns die Drehung um 90° noch einmal ein bisschen genauer an!
|
|
Welche Koordinaten hat der Bildpunkt zu A(12|14) nach der Drehung um den Punkt Z(1|1) mit dem Drehwinkel α = 90°? Berechne die Verbindungvektoren
Tipp [Anzeigen] |
Das war doch gar nicht so schwer, oder? Üben wir das noch einmal an zwei Beispielen!
1. Gib zuerst die Koordinaten des Verbindungsvektor 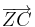 an, wenn der Punkt C(2|14) um den Punkt Z(1|1) um 90° gedreht wird!
an, wenn der Punkt C(2|14) um den Punkt Z(1|1) um 90° gedreht wird!
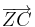 = = |
|
|
Nach dem was du gerade gelernt hast ist es jetzt ganz einfach, die Koordinaten des Vektors 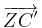 zu berechnen!
zu berechnen!
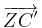 = = |
|
|
2. Das Flugzeug wird jetzt um das Zentrum Z(4|-2) um 90° gedreht. Berechne den Verbindungsvektor 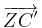 ! (C hat die Koordinaten (2|14)).
! (C hat die Koordinaten (2|14)).
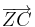 = = |
|
|
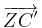 = = |
|
|
Welche Koordinaten hat der Punkt C'?
C' ((x-Koordinate) | (y-Koordinate))
→Du hast das toll gemacht! Auf geht's zur nächsten Teilaufgabe!
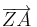 (Urvektor) und
(Urvektor) und 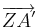 (Bildvektor)!
(Bildvektor)!
