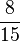Version vom 13. Januar 2010, 08:59 Uhr

2.Station: Multiplikation zweier Brüche

Einführung:

Susi hat am nächsten Tag eine Tafel Schokolade in der Schule dabei!!!
Tom sieht Susi die Schokolade im Klassenzimmer essen und hat sofort auch Heißhunger darauf. Er fragt sie, ob er ein Stück davon haben kann. Susi antwortet: "Ich habe aber nur noch $\frac{4}{5}$ von der Schokolade!!!" Doch weil sie Tom so gern hat gibt sie ihm dann doch noch $\frac{2}{3}$ davon ab!!!

Kreuze nun den richtigen Rechenweg an und klicke auf prüfen!, um zu sehen, ob du Recht hast.

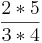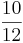(! $\frac{2}{3}$ von $\frac{4}{5}$ = $\frac{2*5}{3*4}$ = $\frac{10}{12}$ = $\frac{5}{6}$ )

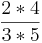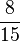( $\frac{2}{3}$ von $\frac{4}{5}$ = $\frac{2*4}{3*5}$ = $\frac{8}{15}$ )

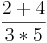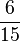( $\frac{2}{3}$ von $\frac{4}{5}$ = $\frac{2 + 4}{3*5}$ = $\frac{6}{15}$ )

Versuche nun die Aufgaben zu lösen und klicke danach auf prüfen! Falsche Antworten werden mit rot angezeigt, richtige mit grün!! Es können auch mehrere Lösungen möglich sein!!!

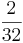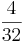$\frac{2}{8}$ * $\frac{2}{4}$ = (! $\frac{2}{32}$ ) ( $\frac{4}{32}$ ) ( $\frac{1}{8}$ )

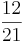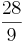$\frac{3}{7}$ * $\frac{4}{3}$ = ( $\frac{12}{21}$ ) ( $\frac{4}{7}$ ) (! $\frac{28}{9}$ )

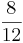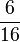$\frac{2}{4}$ * $\frac{4}{3}$ = ( $\frac{8}{12}$ ) ( $\frac{2}{3}$ ) (! $\frac{6}{16}$ )

Ordne die Brüche den richtigen Aufgaben zu oder umgekehrt!!!

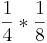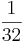$\frac{1}{4} * \frac{1}{8}$	$\frac{1}{32}$
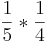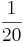$\frac{1}{5} * \frac{1}{4}$	$\frac{1}{20}$
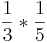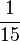$\frac{1}{3} * \frac{1}{5}$	$\frac{1}{15}$
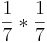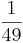$\frac{1}{7} * \frac{1}{7}$	$\frac{1}{49}$

Multiplikation zweier Brüche

Kannst du die Rechenregel nun auch verbal ausdrücken???

Beispiel: $\frac{2}{5}$ * $\frac{3}{4}$

1) Multpliziere die Zähler miteinander.

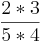
2) Ebenfalls werden die Nenner beider Brüche miteinander multipliziert $\frac{2}{5}$ * $\frac{3}{4}$ = $\frac{2*3}{5*4}$

3) Kürze das Ergebnis soweit wie möglich! 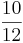$\frac{10}{12}$ = $\frac{5}{6}$

4) Wandle den Bruch (wenn möglich) in einen gemischten Bruchum.

5) Dies alles gilt ebenfalls für Stammbrüche

Zusammenfassung:

Multiplikation zweier Brüche

Man multipliziert zwei Brüche miteinander, indem man die Zähler und die Nenner miteinander multipliziert.
Das Ergebnis kürzt man soweit wie möglich oder wandelt es in einen gemischte Bruch um.

Allgemein:

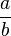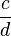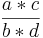
$\frac{a}{b}$ * $\frac{c}{d}$ = $\frac{a*c}{b*d}$

Beispiel oben:

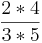$\frac{2}{3}$ * $\frac{4}{5}$ = $\frac{2*4}{3*5}$ = $\frac{8}{15}$

Hier geht`s zur 4. Seite

@@ Zeile 19: / Zeile 19: @@
 <div class="multiplechoice-quiz">
-(!<math> \frac{2}{3} </math> *  <math> \frac{4}{5} </math> = <math> \frac{2*5}{3*4} </math> = <math> \frac{10}{12} </math>  = <math> \frac{5}{6} </math>)
+(!<math> \frac{2}{3} </math>&nbsp; von&nbsp; <math> \frac{4}{5} </math> = <math> \frac{2*5}{3*4} </math> = <math> \frac{10}{12} </math>  = <math> \frac{5}{6} </math>)
-(<math> \frac{2}{3} </math> *  <math> \frac{4}{5} </math>  = <math> \frac{2*4}{3*5} </math> = <math> \frac{8}{15} </math> )
+(<math> \frac{2}{3} </math>&nbsp; von &nbsp; <math> \frac{4}{5} </math>  = <math> \frac{2*4}{3*5} </math> = <math> \frac{8}{15} </math> )
-(<math> \frac{2}{3} </math> *  <math> \frac{4}{5} </math> = <math> \frac{2 + 4}{3*5} </math> = <math> \frac{6}{15} </math>)
+(<math> \frac{2}{3} </math>&nbsp; von &nbsp; <math> \frac{4}{5} </math> = <math> \frac{2 + 4}{3*5} </math> = <math> \frac{6}{15} </math>)
 </div>

Seite 3: Unterschied zwischen den Versionen

Version vom 13. Januar 2010, 08:59 Uhr

2.Station: Multiplikation zweier Brüche

Navigationsmenü

Meine Werkzeuge

Namensräume

Varianten

Ansichten

Aktionen

Suche

Navigation

Werkzeuge