Dreiecke und Winkel: Unterschied zwischen den Versionen
| (6 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
==Teilaufgabe a)== | ==Teilaufgabe a)== | ||
| − | '''Im Applet siehst du <span style="color:#CD2626 ">Spieler<sub>8</sub></span> der Fußballmannschaft „Ballverlust“. <span style="color:#009ACD">Spieler<sub>5</sub></span> und der <span style="color:#009ACD">Torwart</span> gehören zur Mannschaft „Siegreich“.''' | + | '''Im Applet (Zeichenfenster) siehst du <span style="color:#CD2626 ">Spieler<sub>8</sub></span> der Fußballmannschaft „Ballverlust“. <span style="color:#009ACD">Spieler<sub>5</sub></span> und der <span style="color:#009ACD">Torwart</span> gehören zur Mannschaft „Siegreich“.''' |
<quiz display="simple"> | <quiz display="simple"> | ||
| Zeile 20: | Zeile 20: | ||
<quiz display="simple"> | <quiz display="simple"> | ||
{'''Entscheide, welche der folgenden Aussagen richtig sind'''} | {'''Entscheide, welche der folgenden Aussagen richtig sind'''} | ||
| − | - Die Winkel α, β und γ sind die Außenwinkel des Dreiecks | + | - Die Winkel α, β und γ sind die '''Außenwinkel''' des Dreiecks |
| − | + Die Winkel α, β und γ sind die Innenwinkel des Dreiecks | + | + Die Winkel α, β und γ sind die '''Innenwinkel''' des Dreiecks |
| − | + Die Summe der Innenwinkel eines Dreiecks beträgt 180° | + | + Die Summe der Innenwinkel eines Dreiecks beträgt '''180°''' |
| − | - Die Summe der Innenwinkel eines Dreiecks beträgt 150° | + | - Die Summe der Innenwinkel eines Dreiecks beträgt '''150°''' |
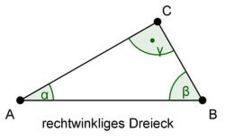
| − | + Hat ein Winkel ein Maß von 90°, nennt man das Dreieck rechtwinklig | + | + Hat ein Winkel ein Maß von 90°, nennt man das Dreieck '''rechtwinklig''' |
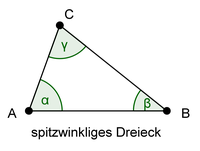
| − | - Ist ein Innenwinkel kleiner als 90°, nennt man das Dreieck spitzwinklig | + | - Ist ein Innenwinkel kleiner als 90°, nennt man das Dreieck '''spitzwinklig''' |
| − | + Sind alle drei Innenwinkelmaße kleiner als 90°, nennt man das Dreieck spitzwinklig | + | + Sind alle drei Innenwinkelmaße kleiner als 90°, nennt man das Dreieck '''spitzwinklig''' |
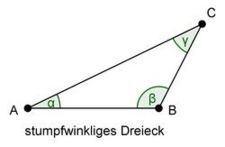
| − | + Ist ein Innenwinkel größer als 90°, nennt man das Dreieck stumpfwinklig | + | + Ist ein Innenwinkel größer als 90°, nennt man das Dreieck '''stumpfwinklig''' |
| − | - Sind zwei Innenwinkel größer als 90°, nennt man das Dreieck stumpfwinklig | + | - Sind zwei Innenwinkel größer als 90°, nennt man das Dreieck '''stumpfwinklig''' |
</quiz> | </quiz> | ||
|} | |} | ||
| Zeile 42: | Zeile 42: | ||
</div> | </div> | ||
| − | '''→[[Kongruenzabbildungen/Parallelverschiebung/Dreiecke_und_Winkel/Seite 2|Hier geht's weiter zur nächsten Teilaufgabe]]''' | + | '''<big>→[[Kongruenzabbildungen/Parallelverschiebung/Dreiecke_und_Winkel/Seite 2|Hier geht's weiter zur nächsten Teilaufgabe]]</big>''' |
Aktuelle Version vom 20. Januar 2010, 12:04 Uhr
Teilaufgabe a)
Im Applet (Zeichenfenster) siehst du Spieler8 der Fußballmannschaft „Ballverlust“. Spieler5 und der Torwart gehören zur Mannschaft „Siegreich“.
Es gibt einiges zu entdecken, wenn Spieler8 auf der Geraden g stürmt. Bewege dazu den Schieberegler.
In dieser Aufgabe wirst du nach spitz-, stumpf- und rechtwinkligen Dreiecken gefragt. Zur Erinnerung kannst du dir hier Bilder dieser Dreiecke anschauen! [Anzeigen]
|
|
|
2. Ordne jetzt die richtigen Werte und Begriffe den Lücken zu!
Der Schieberegler gibt dir die Entfernung des Spielers8 vom Torwart an. Vorsicht: 1LE = 4m!
Spielers8 steht auf der Außenlinie des Spielfeldes um einen Einwurf zu machen. Er ist vom Torwart entfernt. Die drei bilden ein Dreieck. Nach seinem Einwurf stürmt Spielers8 auf der Geraden g in Richtung Torwart. Bewegt er sich außerhalb des Strafraumes, sind alle Innenwinkel des Dreiecks immer als 90°. Befindet er sich jedoch auf der Linie des Strafraumes, entsteht ein Dreieck. Sein Abstand zum Torwart beträgt dann nur noch . Bewegt sich der Spieler innerhalb des Strafraumes, bilden die drei ein Dreieck. Der Winkel γ ist dann immer als 90°.
stumpfwinkligesgrößerkleiner52 m15,2 mrechtwinkligesspitzwinkliges