Beweisführung des Umfangswinkelsatzes: Unterschied zwischen den Versionen

Ich bin der Thales-Clown

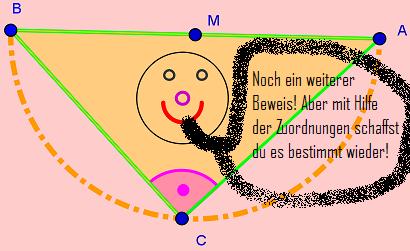
Fünfte Station:

Hast du Lust auf eine Beweisführung?

Klicke mit der linken Maustaste die einzelnen Schritte an!

Auf geht's - viel Spaß beim Zuordnen der Begriffe!

Wenn du möchtest kannst du am Punkt C mit der Maus ziehen.

Zuordnung Ordne den einzelnen Schritten den jeweils passenden Text zu. Schritt 2 Dreieck AMC und Dreieck MBC sind gleichschenklig. (r=r) Schritt 5 Innenwinkelsumme im Dreieck ABC=180°: α + α + β + β = 180° 2α + 2β = 180° α + β = 90° Schritt 3 Schritt 1Basiswinkel sind maßgleich: α = αBasiswinkel sind maßgleich: β = βSchritt 4α + β = γ γ = 90°

Ich bin der Thales-Clown

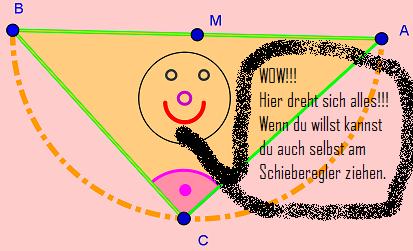
Sechste Station:

Super, du hast die fünfte Station geschafft!

Dann wird die sechste Station dür dich "very easy"!!!

Auf geht's - viel Spaß beim Zuordnen der Begriffe!

Wenn du willst, dann kannst du auch am blauen Punkt C ziehen!

Zuordnung Schritt 5 Schritt 7 Schritt 3 Schritt 2 Schritt 6 Schritt 1 Schritt 4 Wechselwinkel an parallelen Geraden sind gleich groß: α=α und β=β[MA]=[MB]=[MC]: r=r=rNebenwinkel ergänzen sich zu 180°: α+α+β+β=180° 2α+2β=180° α+β=90° γ=90° Innenwinkelsumme im Dreieck: α+β+γ=180° α+β=γ α+β+α+β=180° 2α+2β=180° α+β=90° Dreieck AMC und Dreieck CMB sind gleichschenkligBasiswinkel sind gleich groß: α=α und β=βGerade g ist parallel zu Strecke [AB]

Ich bin der Thales-Clown

Nachdem du die erste Station gemacht hast, kannst du dich jetzt der zweiten Station widmen!

Achte zunächst auf die linke Animation und beobachte den Winkel am roten Eckpunkt!

Wenn du damit fertig bist, dann schaue dir bitte dir rechte Animation an!

Was fällt dir auf, wenn du die Winkel betrachtest?

Um die Fragen zu beantworten, nutze bitte den Multiple-Chpoice-Test!

Viel Spaß dabei!!!

Zweite Station:

Welche Aussagen über die dynamischen Animationen stimmen und welche nicht?