Quadratische Funktionen: Unterschied zwischen den Versionen
(→Quadratische Funktionen) |
(→Aufgabe 2) |
||
| Zeile 74: | Zeile 74: | ||
{| | {| | ||
|- | |- | ||
| − | | [[Bild:Aufgabe3a.png| | + | | [[Bild:Aufgabe3a.png|250px]] || [[Bild:Aufgabe3b.png|250px]] || [[Bild:Aufgabe3c.png|270px]] || [[Bild:Aufgabe3d.png|270px]] |
|- | |- | ||
| <strong> y<math>=</math> 3,5 x<sup>2</sup> </strong> || <strong> y<math>=</math> 2 x<sup>2</sup> </strong> || <strong> y<math>=</math> - 0,1 x<sup>2</sup> </strong> || <strong> y<math>=</math> - x<sup>2</sup> </strong> | | <strong> y<math>=</math> 3,5 x<sup>2</sup> </strong> || <strong> y<math>=</math> 2 x<sup>2</sup> </strong> || <strong> y<math>=</math> - 0,1 x<sup>2</sup> </strong> || <strong> y<math>=</math> - x<sup>2</sup> </strong> | ||
Version vom 16. Februar 2010, 00:06 Uhr
1. Fußball-WM 2006 - Wasserverbrauch
Inhaltsverzeichnis |
Quadratische Funktionen
| Auf der rechten Seite ist eine andere quadratische Funktion abgebildet. Ihr Funktionsterm hat die Form x². Wie wir schon festgestellt haben, unterscheiden sich die Graphen quadratischer Funktionen stark von den Graphen linearer Funktionen.
|
|
|
Im rechten Bild siehst du wieder die Parabel von oben. Man kann für sie auch die Gleichung Aufgabe 1Verändere a mithilfe des Schiebreglers in der nebenstehenden Graphik und beobachte die Veränderung. Als Orientierung dient dir der Graph x². Ist a>0, dann ist die Parabel enger (gestreckt) als die Normalparabel. Für 0< a < 1 ist die Parabel weiter (gestaucht) als die Normalparabel. Ist a negativ, so ist die Parabel nach unten geöffnet . Hast du die Aufgabe gelöst? Präge dir die jeweilige Auswirkung von a gut ein!
|
|
Mit deinen neugewonnenen Erkenntnissen kannst du die nächste Aufgabe lösen.
Aufgabe 2
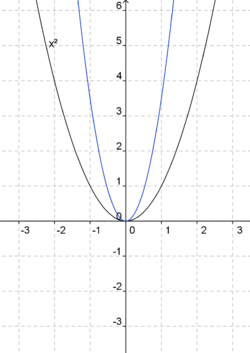
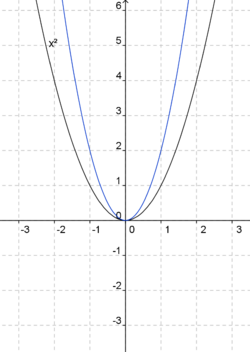
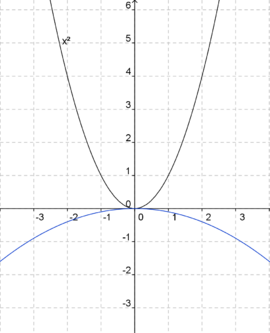
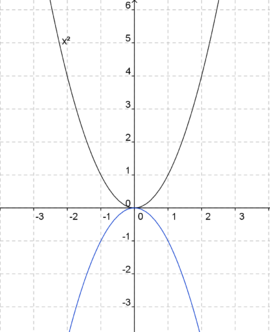
Ordne den blaugefärbten Parabeln die jeweils richtige Gleichung zu. Die Normalparabel (schwarz) dient dir als Orientierung.
.
Aufgabe 3
Kreuze die zutreffenden Aussagen zu obigen quadratischen Funktionen an. Es sind jeweils mehrere Antworten richtig.
f(x) = 3,5x2 (!Die Parabel ist nach unten geöffnet.) (Die Parabel ist nach oben geöffnet.) (Die Parabel ist enger als die Normalparabel.) (!Die Parabel ist weiter als die Normalparabel.) (Der Punkt [2|14] liegt auf dem Graphen.) (Der Punkt [14|2] liegt nicht auf dem Graphen.)
f(x) = -x2 (Die Parabel ist nach unten geöffnet.) (!Die Parabel ist nach oben geöffnet.) (!Die Parabel ist enger als die Normalparabel.) (!Die Parabel ist weiter als die Normalparabel.) (Der Punkt [2|-2] liegt auf dem Graphen.) (!Der Punkt [2|2] liegt auf dem Graphen.)
f(x) = 2x2 (!Die Parabel ist nach unten geöffnet.) (Die Parabel ist nach oben geöffnet.) (Die Parabel ist enger als die Normalparabel.) (!Die Parabel ist weiter als die Normalparabel.) (!Der Punkt [0|-2] liegt auf dem Graphen.) (Der Punkt [1|2] liegt oberhalb des Graphen.)
f(x) = -0,1x2 (Die Parabel ist nach unten geöffnet.) (!Die Parabel ist nach oben geöffnet.) (!Die Parabel ist enger als die Normalparabel.) (Die Parabel ist weiter als die Normalparabel.) (!Der Punkt [-1|2] liegt auf dem Graphen.) (Der Punkt [-1|1] liegt oberhalb des Graphen.)
.
Bevor wir zum nächsten Kapitel gehen, hast du hier noch einmal die Möglichkeit alles wichtige zusammengefasst zu wiederholen:
|
Merke:
Die Graphen von Funktionen mit der Funktionsgleichung Sie sind symmetrisch zur y-Achse. Der Punkt Ist a=1 heißt der dazugehörige Graph Normalparabel. |

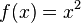 heißen Parabeln.
heißen Parabeln.
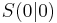 heißt Scheitel der Parabel und ist der tiefste Punkt.
heißt Scheitel der Parabel und ist der tiefste Punkt.
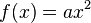 aufstellen, wobei
aufstellen, wobei 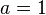 ist. In diesem Fall heißt die Funktion Normalparabel. Doch was passiert, wenn man die Zahl a verändert?
ist. In diesem Fall heißt die Funktion Normalparabel. Doch was passiert, wenn man die Zahl a verändert?
 3,5 x2
3,5 x2  nächstes Kapitel
nächstes Kapitel Zurück zur WM 2006
Zurück zur WM 2006
