Grundlagen der Zerlegungsgleichheit von Figuren: Unterschied zwischen den Versionen
(→1.2 Los geht´s: Teste Dein Wissen!) |
K |
||
| Zeile 10: | Zeile 10: | ||
---- | ---- | ||
<br> | <br> | ||
| − | Weißt Du noch was man unter '''Kongruenz von Figuren''' versteht?? | + | Weißt Du noch was man unter <span style="color:#00CD00">'''Kongruenz von Figuren'''</span> versteht?? |
| − | Eine Wiederholung kann nicht schaden | + | Eine Wiederholung kann nicht schaden. |
===1.2 Los geht´s: Teste Dein Wissen!=== | ===1.2 Los geht´s: Teste Dein Wissen!=== | ||
| Zeile 21: | Zeile 21: | ||
</div> | </div> | ||
<br> | <br> | ||
| − | '''Hinweis''': ''Kongruente'' Figuren kann man zur ''Deckung'' bringen | + | '''Hinweis''': <span style="color:#00CD00">'''Kongruente'''</span> Figuren kann man zur <span style="color:#00CD00">'''Deckung'''</span> bringen |
---- | ---- | ||
| Zeile 31: | Zeile 31: | ||
====Aufgabe: Kongruente Dreiecke==== | ====Aufgabe: Kongruente Dreiecke==== | ||
<br> | <br> | ||
| − | Findest Du alle Dreiecke, die zum Dreieck A kongruent sind?<br>Gib die Buchstaben an und begründe warum. | + | '''Findest Du alle Dreiecke, die zum Dreieck A kongruent sind?'''<br>'''''Gib die Buchstaben an und begründe anschließend warum.''''' |
<br> | <br> | ||
[[Bild:Ebert_imageKongruenteDreiecke.jpg]] | [[Bild:Ebert_imageKongruenteDreiecke.jpg]] | ||
<br> | <br> | ||
| − | + | <quiz display="simple"> | |
| − | Kongruente Dreiecke zu A sind | + | {Kongruente Dreiecke zu A sind?} |
| − | + | -B und D | |
| − | + | +C und E | |
| − | Welche Dreiecke sind ähnlich zu A?? | + | +G und H |
| − | + | -J und K | |
| + | -I und F | ||
| + | |||
| + | {Welche Dreiecke sind ähnlich zu A??} | ||
| + | -B und F | ||
| + | +C | ||
| + | +D | ||
| + | +E und G | ||
| + | +H | ||
| + | -I | ||
| + | -J | ||
| + | +K | ||
| + | </quiz> | ||
<br> | <br> | ||
<br> | <br> | ||
| − | War Deine Lösung richtig? | + | War Deine Lösung richtig? |
---- | ---- | ||
====Kleines Quiz==== | ====Kleines Quiz==== | ||
| − | Achtung!! Mehrere Antworten sind möglich! | + | '''''Achtung!! Mehrere Antworten sind möglich!''''' |
<quiz display="simple"> | <quiz display="simple"> | ||
{ Markiere die richtigen Antworten} | { Markiere die richtigen Antworten} | ||
| − | - alle zueinander ähnlichen Figuren sind zueinander kongurent | + | - alle zueinander '''ähnlichen''' Figuren sind zueinander '''kongurent''' |
| − | + alle zueinander kongruenten Figuren sind zueinander ähnlich | + | + alle zueinander '''kongruenten''' Figuren sind zueinander '''ähnlich''' |
| − | - alle kongruenten Figuren haben die gleiche Farbe | + | - alle '''kongruenten''' Figuren haben die '''gleiche Farbe''' |
| − | + alle kongruenten Figuren haben den gleichen Flächeninhalt | + | + alle '''kongruenten''' Figuren haben den '''gleichen Flächeninhalt''' |
</quiz> | </quiz> | ||
| Zeile 110: | Zeile 122: | ||
---- | ---- | ||
[[Bild:Ebert_KapitänCheckInsel.jpg|center]] | [[Bild:Ebert_KapitänCheckInsel.jpg|center]] | ||
| − | <br> | + | <br>'''Aufgabenstellung''' Ziehe mit der linken Maustaste die unten stehenden Figuren auf die Insel- Umrisse, so dass diese bedeckt werden. |
| + | |||
<br> | <br> | ||
(''Geogebra-Applet mit Insel-Umrissen'') | (''Geogebra-Applet mit Insel-Umrissen'') | ||
<br> | <br> | ||
| − | |||
| − | Was fällt Dir auf? Welche ist dir größte Insel?? Begründe Deine Antwort! | + | '''''Was fällt Dir auf? Welche ist dir größte Insel??''' Begründe Deine Antwort!'' |
<quiz display="simple"> | <quiz display="simple"> | ||
{Markiere die richtige Antwort:} | {Markiere die richtige Antwort:} | ||
| Zeile 127: | Zeile 139: | ||
</quiz> | </quiz> | ||
| − | Begründung: | + | '''Begründung:''' |
<u style="color:lightgrey;background:lightgrey">Die Figuren A und C sind gleich groß, da sie mit sechs Teilfiguren ausgelegt werden können, die jeweils kongruent zueinander sind. | <u style="color:lightgrey;background:lightgrey">Die Figuren A und C sind gleich groß, da sie mit sechs Teilfiguren ausgelegt werden können, die jeweils kongruent zueinander sind. | ||
<br>Figur B kann mit einer Teilfigur mehr ausgelegt werden, deshalb ist sie die größte der drei Inseln.</u> | <br>Figur B kann mit einer Teilfigur mehr ausgelegt werden, deshalb ist sie die größte der drei Inseln.</u> | ||
Version vom 27. Juni 2009, 09:44 Uhr
Auf dieser Seite lernst Du die Eigenschaften der Zerlegungsgleichheit von Figuren kennen.
Bearbeite die Aufgaben sorgfältig!
Nicht mogeln...schaue erst die Lösungen an, wenn du die Aufgaben selbstsändig bearbeitet hast!
Denn nur so lernst du am Besten!
1. Grundlagen der Zerlegungsgleichheit von Figuren
1.1 Wiederholung des Kongruenzbegriffes
Weißt Du noch was man unter Kongruenz von Figuren versteht??
Eine Wiederholung kann nicht schaden.
1.2 Los geht´s: Teste Dein Wissen!
Ein anderes Wort für Kongruenz ist Deckungsgleichheit
Hinweis: Kongruente Figuren kann man zur Deckung bringen
Aufgabe: Wie erzeugt man kongruente Figuren?
Aufgabe: Kongruente Dreiecke
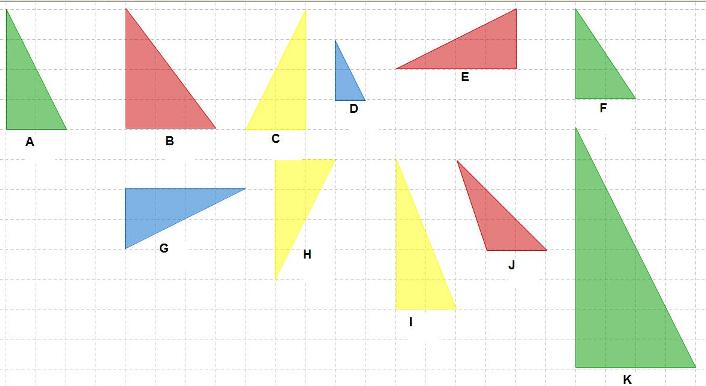
Findest Du alle Dreiecke, die zum Dreieck A kongruent sind?
Gib die Buchstaben an und begründe anschließend warum.
War Deine Lösung richtig?
Kleines Quiz
Achtung!! Mehrere Antworten sind möglich!
1.3 Das sollest du also wissen
| Zwei Figuren sind zueinander kongruent, wenn sie durch Verschiebung,Drehung oder Spiegelung ineinander überführt werden können. Diese drei Abbildungen nennt man daher auch Kongruenz-abbildungen. |
1.4 Wofür können wir die Kongruenz von Figuren gebrauchen?
Du kennst sicher ein paar Anwendungsbeispiele wofür man die Eigenschaften der
Kongruenz von Figuren nutzen kann. (wird evt. später noch eingefügt: Kongruenz von Dreiecken, Konstruktionen)
Im nächsten Abschnitt lernst Du ein weiteres Anwendungsbeispiel kennen
2. Zerlegungsgleichheit von Figuren
2.1 Eine Einführung
Kennst Du den Namen des Legespiels?
</div>
Aufgabe: Teilfiguren finden
Hier siehts Du drei Figuren: Eine Schiffskatze, ein Papagei und ein Matrose.
Sie alle lassen sich in Teilfiguren zerlegen.
Aufgabenstellung: Finde die Teilfiguren, indem Du die Linien (genauere Hilfestellung wird noch gegeben) einzeichnest.
GeoGebra-Applet mit Tangram-Figuren
Prima!!! Du hast nun alle Teilfiguren entdeckt.
Was fällt Die beim Vergleich der Figuren auf?
Tipp: Achte auf Anzahl und Eigenschaften der Teilfiguren (wird noch formatiert)
Lösung: Die Figuren bestehen aus der gleichen Anzahl an Teilfiguren, welche jeweils paarweise kongruent zueinander sind.
Kapitän Check Aufgabe: Welche ist die größte Insel?
Aufgabenstellung Ziehe mit der linken Maustaste die unten stehenden Figuren auf die Insel- Umrisse, so dass diese bedeckt werden.
(Geogebra-Applet mit Insel-Umrissen)
Was fällt Dir auf? Welche ist dir größte Insel?? Begründe Deine Antwort!
Begründung:
Die Figuren A und C sind gleich groß, da sie mit sechs Teilfiguren ausgelegt werden können, die jeweils kongruent zueinander sind.
Figur B kann mit einer Teilfigur mehr ausgelegt werden, deshalb ist sie die größte der drei Inseln.
| Figur A und C nennt man daher auch zerlegungsgleich, |
2.3 Das Prinzip der Zerlegungsgleichheit
Die nebenstehenden Figuren (Bild wird noch eingefügt) wurden in jeweils vier Teilfiguren zerlegt.
Diese Teilfiguren sind paarweise zueinander kongruent, d.h. es gibt immer ein Paar zueinander kongruenter Figuren.
Aus den Eigenschaften der Kongruenz ergibt sich daher, dass diese den gleichen Flächeninhalt besitzen.
Die Quadratfläche setzt sich aus den Teilflächen (...) zusammen
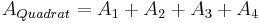
Es gilt aber auch 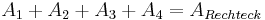
| sich aus der Addition der Flächeninhalte der Teilfiguren |
| Das ist ja klasse!! Wir können feststellen, dass zwei Figuren den gleichen Flächeninhalt besitzen, obwohl wir den Flächeninhalt der einzelnen Teilflächen selbst noch gar nicht berechnen können! |
Hierzu ein kleines Beispiel:
Kannst Du zeigen, dass die beiden folgenden Figuren den gleichen Flächeninhalt haben?
Hier findest du den Hinweis
- Übertrage folgende Definition in Dein Heft:
| Man kann die Berechnung des Flächeninhaltes von Figuren, für die man keine Berechnungsformel kennt, auf Figuren zurückführen, für die man eine Flächeninhaltsformel kennt. |