Quadratische Funktionen: Unterschied zwischen den Versionen
(→Aufgabe x) |
(→Quadratische Funktionen) |
||
| Zeile 40: | Zeile 40: | ||
Mit der Manipulation des Schiebereglers hast du a verändert. | Mit der Manipulation des Schiebereglers hast du a verändert. | ||
Die Auswirkungen von unterschiedlichen Werten für a kannst du in der nebenstehenden Abbildung noch einmal testen. | Die Auswirkungen von unterschiedlichen Werten für a kannst du in der nebenstehenden Abbildung noch einmal testen. | ||
| − | + | ||
| − | + | ||
| Zeile 47: | Zeile 46: | ||
===Aufgabe 1=== | ===Aufgabe 1=== | ||
| − | + | Hast du mit a etwas experimentiert?<br\> | |
| − | + | Dann wird es dir jetzt nicht mehr schwer fallen, diese Sätze zu vervollständigen. | |
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
| − | Ist a>0, dann ist die Parabel <strong> enger </strong> (gestreckt) als die Normalparabel. | + | Ist a > 0, dann ist die Parabel <strong> enger </strong> (gestreckt) als die Normalparabel. |
| − | Für 0< a < 1 ist die Parabel <strong> weiter </strong> (gestaucht) als die Normalparabel. | + | Für 0 < a < 1 ist die Parabel <strong> weiter </strong> (gestaucht) als die Normalparabel. |
Ist a negativ, so ist die Parabel <strong> nach unten geöffnet </strong>. | Ist a negativ, so ist die Parabel <strong> nach unten geöffnet </strong>. | ||
| Zeile 65: | Zeile 64: | ||
|valign="top"| | |valign="top"| | ||
| − | <ggb_applet width=" | + | <ggb_applet width="600" height="600" version="3.2" ggbBase64="UEsDBBQACAAIAHCtUzwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1svVbbbtw2EH1uvoJQgSAp6rUuu+tdZOUgzUNqwG0CbOqHPBSgpJHEmiK3vNhaf0++oJ/Q/FiHpLQXwzUMuOiTJHI4l3PmjLh623ec3IDSTIo8SiZxRECUsmKiySNr6pNF9Pb8xaoB2UChKKml6qjJo2ySRm7dsvMX3610K28J5d7kisFtHtWUa4iI3iiglW4BzNE6tT3jjKrtx+IPKI3ebwQnF2JjMYpRFtfKrrpkevw8dQFrKQwhmt0BJj13a6tTn8sKbMlZxahw8XxuaETILatMm0eLxTQiLbCmRXezOAveSilVtd5qAx3pv4CSeZTG2WQ6S9NptpwtZmdZjOe2YStLZg4mXVIOzslkMc/iebxcLOfTLJ2j3X4rDgHgZg3GIKaa0B70WFijWHX4fqF/krzaYbGRTJj3dGOs8nRkw9LabJ17zEG5Qt6JhsOwliJaLZTXhezXAZwsuP683fgjPp2ieS+5VEThgdkMDYZnEZ7exuW5s4q9TewtBh/O6W4/Wabewj+L8PRWnImQ2lB3MhadxGMYpolbcIhiF41wcFoAz6OIWMHM5fhhWHk9VJoE+19tV2D3HvbGzmXyH7lcnd5rqtU1KAE8tI5AXq20mtxQPlLn86igZB1+ho0BEOrI+g0TCKsVNArGvEPrB7j8bnzYnveWV6djEi4HjbmWBjWM9RhXi5OYaSVyc6FdqZxcoYJ5RCpq3LZTCocOUEbGt4awHShW7mCikQuN8ewQNRmb2Ytdet3eg3bPAW4/2Dyp0xHlm5biyiQZmoRuQR1V7P39Iqsx9BAYOUDDjuGkOvEa7GiPMnNvtNCSWwPrEvEUl7Kkxk+0kN+g/iR2iiR4Jp26ly2+LDP3VrMe9sJD3NgdEkuPatr3smmxaQRo7QVnDqVFBXLuicBpsnFFxq6tNuDc+/E6mpMN1u11vesZbLTAiWOnx9Gp3VgO6JI8anA29+izedW/Jjnpf3+VTuLX/uAxl7UVvhl2xDTRkwt4DrvxAbfxo9x+rGsNxjGx9DTM0geJT/8N1Kdj+qSyHwMefQ241wF3Sn7YYU+eAH79/4B/LK2nwu/+D4j/2fIx4T0bwc/Qm2RA8eWfVpo3X6z49rVstcGfOLhHZVGl4PRdMSCfqPJN3+GgdGsvv0/iNx84sLK1oiGOibz/+68fcZwRmicTcgXq21eBpvin8ad+ZryGcK4CTdZlywDHOuD4VdqKihQgC1q2BnzAd1bfMnXtnPsz1NYYWJAPim5aEJOQ9QNaM1hadFzn40wedObzdbSnKj64GGmc5PX+DuYvAifIlx7/c6HZDFXmk7tQENcJKKrF2VkyXWZpks7ny0UalDlxL3e7+X9I9Onhn8dfwYZr4vk/UEsHCGBOYi8CBAAAWAoAAFBLAQIUABQACAAIAHCtUzxgTmIvAgQAAFgKAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAPAQAAAAA" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" /> |
| − | + | ||
| − | + | ||
|} | |} | ||
Version vom 19. Februar 2010, 21:49 Uhr
1. Fußball-WM 2006 - Wasserverbrauch
Inhaltsverzeichnis |
Quadratische Funktionen
Aufgabe x
|
Bei der Suche nach einer passenden Sprungbahn ist dir sicherlich aufgefallen, dass sich der Name der Funktion geändert hat. Vor dem x² ist plötzlich eine Zahl erschienen. Unsere Funktione erhält also eine neue Geleichung:
Aufgabe 1Hast du mit a etwas experimentiert? Ist a > 0, dann ist die Parabel enger (gestreckt) als die Normalparabel. Für 0 < a < 1 ist die Parabel weiter (gestaucht) als die Normalparabel. Ist a negativ, so ist die Parabel nach unten geöffnet . Hast du die Aufgabe gelöst? Präge dir die jeweilige Auswirkung von a gut ein!
|
|
Mit deinen neugewonnenen Erkenntnissen kannst du die nächste Aufgabe lösen.
Aufgabe 2
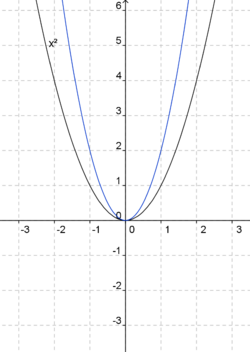
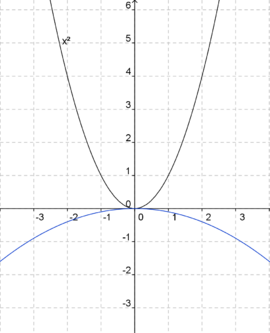
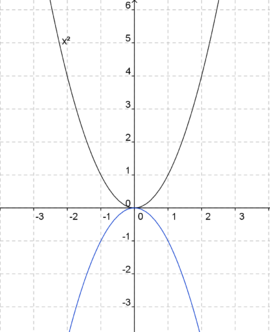
Ordne den blaugefärbten Parabeln die jeweils richtige Gleichung zu. Die Normalparabel (schwarz) dient dir als Orientierung.
.
Aufgabe 3
Kreuze die zutreffenden Aussagen zu obigen quadratischen Funktionen an. Es sind jeweils mehrere Antworten richtig.
f(x) = 3,5x2 (!Die Parabel ist nach unten geöffnet.) (Die Parabel ist nach oben geöffnet.) (Die Parabel ist enger als die Normalparabel.) (!Die Parabel ist weiter als die Normalparabel.) (Der Punkt [2|14] liegt auf dem Graphen.) (Der Punkt [14|2] liegt nicht auf dem Graphen.)
f(x) = -x2 (Die Parabel ist nach unten geöffnet.) (!Die Parabel ist nach oben geöffnet.) (!Die Parabel ist enger als die Normalparabel.) (!Die Parabel ist weiter als die Normalparabel.) (Der Punkt [2|-2] liegt auf dem Graphen.) (!Der Punkt [2|2] liegt auf dem Graphen.)
f(x) = 2x2 (!Die Parabel ist nach unten geöffnet.) (Die Parabel ist nach oben geöffnet.) (Die Parabel ist enger als die Normalparabel.) (!Die Parabel ist weiter als die Normalparabel.) (!Der Punkt [0|-2] liegt auf dem Graphen.) (Der Punkt [1|2] liegt oberhalb des Graphen.)
f(x) = -0,1x2 (Die Parabel ist nach unten geöffnet.) (!Die Parabel ist nach oben geöffnet.) (!Die Parabel ist enger als die Normalparabel.) (Die Parabel ist weiter als die Normalparabel.) (!Der Punkt [-1|2] liegt auf dem Graphen.) (Der Punkt [-1|1] liegt oberhalb des Graphen.)
.
Bevor wir zum nächsten Kapitel gehen, hast du hier noch einmal die Möglichkeit alles wichtige zusammengefasst zu wiederholen:
|
Merke:
Die Graphen von Funktionen mit der Funktionsgleichung Sie sind symmetrisch zur y-Achse. Der Punkt Ist a=1 heißt der dazugehörige Graph Normalparabel. |
Alles klar? Dann kann's ja weitergehen.

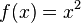 heißen Parabeln.
heißen Parabeln.
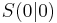 heißt Scheitel der Parabel und ist der tiefste Punkt.
heißt Scheitel der Parabel und ist der tiefste Punkt.
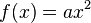 .
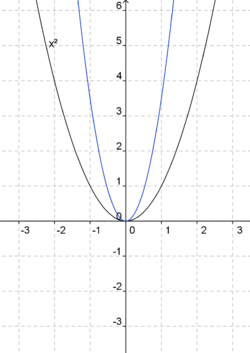
Mit der Manipulation des Schiebereglers hast du a verändert.
Die Auswirkungen von unterschiedlichen Werten für a kannst du in der nebenstehenden Abbildung noch einmal testen.
.
Mit der Manipulation des Schiebereglers hast du a verändert.
Die Auswirkungen von unterschiedlichen Werten für a kannst du in der nebenstehenden Abbildung noch einmal testen.
 3,5 x2
3,5 x2  nächstes Kapitel
nächstes Kapitel Zurück zur WM 2006
Zurück zur WM 2006
