übungen zur Scheitelpunktform: Unterschied zwischen den Versionen
(→Bestimmen der Scheitelpunktsform mit a) |
|||
| Zeile 8: | Zeile 8: | ||
;Aufgabe 16 | ;Aufgabe 16 | ||
Bei all diesen Funktionsgraphen hat a wieder den Wert 1.<br/> Ordne den Graphen die richtige Funktion zu. | Bei all diesen Funktionsgraphen hat a wieder den Wert 1.<br/> Ordne den Graphen die richtige Funktion zu. | ||
| − | Tipp: Denke daran, dass die Form | + | Tipp: Denke daran, dass die Form y=a(x '''-''' x<sub>s</sub>)<sup>2</sup>+y<sub>s</sub> lautet, das bedeutet, wenn vor x<sub>s</sub> '''in der Klammer ein Minus steht, so ist x<sub>s</sub> ''' '''größer als Null'''. <br/> Steht vor x<sub>s</sub> '''in der Klammer ein Plus, so isx<sub>s</sub> ''' '''größer''' als Null. |
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
Version vom 20. Februar 2010, 22:17 Uhr
Vom Graphen zur Funktion
- Aufgabe 16
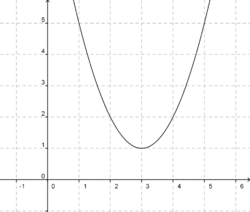
Bei all diesen Funktionsgraphen hat a wieder den Wert 1.
Ordne den Graphen die richtige Funktion zu.
Tipp: Denke daran, dass die Form y=a(x - xs)2+ys lautet, das bedeutet, wenn vor xs in der Klammer ein Minus steht, so ist xs größer als Null.
Steht vor xs in der Klammer ein Plus, so isxs größer als Null.
Bestimmen der Scheitelpunktsform mit a
Doch wie schaut das aus, wenn der Parameter a nicht eins ist? Wie kriegst du den heraus? Auch das ist ganz einfach. Dafür brauchst du den Scheitel, um xs und ys ablesen zu können, und einen zweiten Punkt. Ich verdeutliche dir dies an einem Beispiel.
|
Bei der Parabel rechts hat der Scheitel S die Koordinaten (-1/3). Außerdem ist der Punkt P, der auf der Parabel liegt, gegeben. P hat die Koordinaten (-2/1). Nun soll die Funktion der Parabel gefunden werden. Dafür setze ich zuerst die Koordinaten von S in die Scheitelpunktsform ein. Man erhält: |
|
Mit diesem Verfahren kannst du nun jede quadratische Funktion bestimmen, solange du ihren Scheitel kennst und und die Koordinaten eines Punktes, der auf der Parabel der Funktion liegt.



 [x-2]2 -2
[x-2]2 -2 
