Parameter a: Unterschied zwischen den Versionen
Aus DMUW-Wiki
| Zeile 4: | Zeile 4: | ||
= Der Parameter a = | = Der Parameter a = | ||
| − | <div style="border: 2px solid white; background-color: | + | <div style="border: 2px solid white; background-color:white; padding:7px;"> |
Nachdem du jetzt f(x)=x<sup>2</sup> schon kennst, erweitern wir das ein bisschen. | Nachdem du jetzt f(x)=x<sup>2</sup> schon kennst, erweitern wir das ein bisschen. | ||
Man kann eine quadratische Funktion auch durch die Formel f(x)=ax<sup>2</sup> ausdrücken. | Man kann eine quadratische Funktion auch durch die Formel f(x)=ax<sup>2</sup> ausdrücken. | ||
Version vom 21. Februar 2010, 19:44 Uhr
Der Parameter a
Nachdem du jetzt f(x)=x2 schon kennst, erweitern wir das ein bisschen. Man kann eine quadratische Funktion auch durch die Formel f(x)=ax2 ausdrücken. Für welches a erhält man dann wohl die Normalparabel als Graph?
Man erhält eine Normalparabel, wenn a = 1(Zahl eintragen) ist.
Finde in der nächsten Aufgabe heraus, was a bei einer Parabel bewirkt.
- Aufgabe 6
|
|
Für a gleich eins erhältst du die Normalparabel. Ist a > 1, so ist die Parabel |
- Aufgabe 7
Zuordnung
Ordne die Funktionen den richtigen Graphen zu und den Graphen die richtigen Funktionen zu.
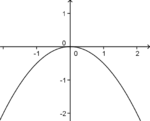 |
f(x)= -0,5x2 |
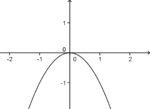 |
f(x)= -x2 |
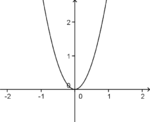 |
f(x)= 3x2 |
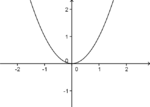 |
f(x)= x2 |
- Aufgabe 8

