Station 1: Unterschied zwischen den Versionen
Aus DMUW-Wiki
< Lernpfade | Winkelhalbierende | Lernpfad 2
| (10 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | Zu ersteinmal | + | Du bearbeitest Lernpfad 2. |
| + | <br /> | ||
| + | |||
| + | ---- | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <br /> | ||
| + | Zu ersteinmal wollen wir uns noch einmal genau ins Gedächtnis rufen, was denn eine Ortslinie eigentlich ist: | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| Zeile 8: | Zeile 15: | ||
{{Definition|Eine Ortslinie ist die Menge aller Punkte, die gemeinsame Eigenschaften haben.}} | {{Definition|Eine Ortslinie ist die Menge aller Punkte, die gemeinsame Eigenschaften haben.}} | ||
<br /> | <br /> | ||
| − | |||
| − | |||
| − | |||
<br /> | <br /> | ||
Zum Beispiel: | Zum Beispiel: | ||
| Zeile 20: | Zeile 24: | ||
[[Bild:Ortslinie1_Herr.jpg]] | [[Bild:Ortslinie1_Herr.jpg]] | ||
<br /> | <br /> | ||
| − | Damit | + | Damit erhälst du eine '''Parallele''' zu g im Abstand d = 3cm. |
<br /> | <br /> | ||
<br /> | <br /> | ||
| Zeile 29: | Zeile 33: | ||
<br /> | <br /> | ||
<br /> | <br /> | ||
| − | Alle Punkte P, die vom Punkt A und vom Punkt B den '''selben Abstand''' haben. | + | Alle Punkte P, die vom Punkt A und vom Punkt B den '''selben Abstand a''' haben (dabei ist es egal, wie groß a ist). |
<br /> | <br /> | ||
<br /> | <br /> | ||
| − | [[Bild:Ortslinie2_Herr. | + | [[Bild:Ortslinie2_Herr.JPG]] |
<br /> | <br /> | ||
| − | Damit erhälts du die Mittelsenkrechte auf die Strecke [AB] | + | Damit erhälts du die '''Mittelsenkrechte''' auf die Strecke [AB] |
<br /> | <br /> | ||
<br /> | <br /> | ||
| + | <br /> | ||
| + | |||
| + | ---- | ||
| + | <br /> | ||
| + | [[../Station 2|Hier gehts es weiter...]]<br> | ||
<br /> | <br /> | ||
Aktuelle Version vom 25. März 2010, 07:52 Uhr
Du bearbeitest Lernpfad 2.
Zu ersteinmal wollen wir uns noch einmal genau ins Gedächtnis rufen, was denn eine Ortslinie eigentlich ist:
Ortslinien
Definition
Eine Ortslinie ist die Menge aller Punkte, die gemeinsame Eigenschaften haben.
Zum Beispiel:
Alle Punkte P, die von der Geraden g den selben Abstand d = 3cm haben.
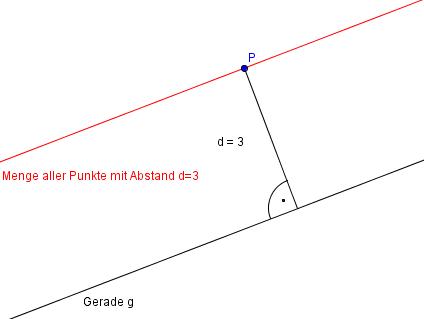
Damit erhälst du eine Parallele zu g im Abstand d = 3cm.
Ein weiteres Beispiel:
Alle Punkte P, die vom Punkt A und vom Punkt B den selben Abstand a haben (dabei ist es egal, wie groß a ist).
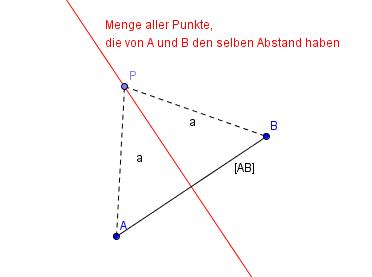
Damit erhälts du die Mittelsenkrechte auf die Strecke [AB]

