Potenzfunktionen: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
Zeile 5: Zeile 5:
  
 
Hier eine Aufgabe, die bereits Mathematik aus verschiedenen Bereichen verbindet und Prüfungsaufgaben ähnelt.
 
Hier eine Aufgabe, die bereits Mathematik aus verschiedenen Bereichen verbindet und Prüfungsaufgaben ähnelt.
 +
 +
==Aufgabe mit einer Hyperbel==
 +
Gegeben ist die Funktion f ,mit<math> y=3 \cdot x^{-1} -4 (\mathbb{G}=\mathbb{R^+}\times\mathbb{R})</math>
 +
<quiz display="simple">
 +
{[[Bild:Peter_Fischer_Papier.png|40px]]
 +
| type="{}" }
 +
*Gib die Wertemenge der Funktion an. <math>\mathbb{W}=\{y|y></math>{ -4 _5}}
 +
 +
*Tabellarisiere f für <math>x\in \{0,5; 1; 2; 3; 4; 5; 6}</math> und zeichne den Graphen in ein Koordinatensystem.
 +
Für die Zeichnung:  <math>1 LE = 1 cm; -3\leg x \leg 7; -11\leg y \leg 3</math>
 +
</quiz>
 +
  
 
==Aufgabe mit Funktion <math>f_(x)=x^3</math>==
 
==Aufgabe mit Funktion <math>f_(x)=x^3</math>==
Zeile 14: Zeile 26:
 
</popup>
 
</popup>
  
−
*Berechne den Flächeninhalt des Quadrates A<sub>2</sub>B<sub>2</sub>C<sub>2</sub>D<sub>2</sub>, wenn A<sub>2</sub> auf der Geraden g mit y=-x liegt.
+
*Berechne den Flächeninhalt des Quadrates A<sub>2</sub>B<sub>2</sub>C<sub>2</sub>D<sub>2</sub>, wenn A<sub>2</sub> auf der Geraden g mit y= -x liegt.
−
<quiz>
+
<quiz display="simple">
 
{[[Bild:Peter_Fischer_Papier.png|40px]]  
 
{[[Bild:Peter_Fischer_Papier.png|40px]]  
 
| type="{}" }
 
| type="{}" }
−
Der Flächeninhalt beträgt A={ 2 _5}[FE]
+
Der Flächeninhalt beträgt A<sub> A<sub>2</sub>B<sub>2</sub>C<sub>2</sub>D<sub>2</sub></sub>={ 2 _5}[FE]
−
<popup name="Lösungsschritte">  
+
<popup name="Lösungsschritte"> *Schnittpunkt A<sub>2</sub> zwischen y= -x und f(x) durch Gleichsetzen berechnen. Länge der Strecke <math>\overline{AO}</math> mit der Formel, Länge eines Vektors (<math>l=\sqrt{v^2_x+v^2_y}</math> berechnen. Mit Pythagoras aus der Diagonalenlänge die Kantenlänge a des Quadrates  berechen. Die Fläche mit Hilfe von <math>A=a^2</math> ermitteln
  
−
</popup>
+
*Ermittle die nach y Aufgelöste Gleichung der Umkehrfunktion f<sup>-1</sup> zu f.
 +
f<sup>-1</sup>: <math>y=\frac{1}{\sqrt[3]{-x}}</math>
  
 
</quiz>
 
</quiz>
 +
 +
  
 
Weiter gehts zu [[Potenzfunktoinsabbildungen]]  
 
Weiter gehts zu [[Potenzfunktoinsabbildungen]]  

Version vom 27. Mai 2010, 08:44 Uhr

Potenzfunktionen

{{#slideshare:potenzfunktion-100520132023-phpapp01}}

Hier eine Aufgabe, die bereits Mathematik aus verschiedenen Bereichen verbindet und Prüfungsaufgaben ähnelt.

Aufgabe mit einer Hyperbel

Gegeben ist die Funktion f ,mit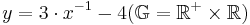 y=3 \cdot x^{-1} -4 (\mathbb{G}=\mathbb{R^+}\times\mathbb{R})

1. Peter Fischer Papier.png

*Gib die Wertemenge der Funktion an. \mathbb{W}=\{y|y>}
*Tabellarisiere f für Fehler beim Parsen(Syntaxfehler): x\in \{0,5; 1; 2; 3; 4; 5; 6} und zeichne den Graphen in ein Koordinatensystem.
Für die Zeichnung: Fehler beim Parsen(Unbekannte Funktion „\leg“): 1 LE = 1 cm; -3\leg x \leg 7; -11\leg y \leg 3

Punkte: 0 / 0


Aufgabe mit Funktion 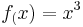f_(x)=x^3

Der Hyperbelast h ist der Graph der Funktion f mit 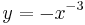y=-x^{-3} mit der Definitionsmenge 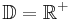\mathbb{D}=\mathbb{R^+}. Der Punkt 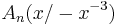A_n(x/-x^{-3}) ist Eckpunkt von Quadraten 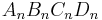A_nB_nC_nD_n mit dem Symmetriepunkt O(0/0).

Hier ist ein Applet zur anschaulichen DarstellungPeter Fischer Applet.png

  • Berechne den Flächeninhalt des Quadrates A2B2C2D2, wenn A2 auf der Geraden g mit y= -x liegt.

1. Peter Fischer Papier.png

Der Flächeninhalt beträgt A A2B2C2D2=[FE]
*Ermittle die nach y Aufgelöste Gleichung der Umkehrfunktion f-1 zu f.
f-1: y=\frac{1}{\sqrt[3]{-x}}

Punkte: 0 / 0



Weiter gehts zu Potenzfunktoinsabbildungen

Potenzen und Potenzfunktionen
LERNPFAD | Potenzen und Potenzfunktionen | Exkurs Lineare Funktionen | Exkurs Quadratische Funktionen | Potenzfunktionen | Potenzfunktoinsabbildungen
Von „http://dmuw.zum.de/index.php?title=Lernpfade/Prüfungsvorbereitung/Potenzen_und_Potenzfunktionen/Potenzfunktionen&oldid=19303“