5.Station: Unterschied zwischen den Versionen
Aus DMUW-Wiki
K |
|||
| Zeile 1: | Zeile 1: | ||
__NOTOC__ | __NOTOC__ | ||
| + | <div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;"> | ||
| + | [[Benutzer:Leonie Porzelt/Abbildung durch zentrische Streckung|1. Station: Ähnlichkeitsabbildung]] - [[Benutzer:Leonie Porzelt/Abbildung durch zentrische Streckung/Hier kannst du weitere Beispiele einer zentrischen Streckung sehen|Exkurs: Weitere Beispiele einer zentrischen Streckung]] - [[Benutzer:Leonie Porzelt/Abbildung durch zentrische Streckung/2.Station|2. Station: Streckungsfaktor]] - [[Benutzer:Leonie Porzelt/Abbildung durch zentrische Streckung/3.Station|3. Station: Berechnung der Streckenlängen und des Streckungsfaktors]] - [[Benutzer:Leonie Porzelt/Abbildung durch zentrische Streckung/4.Station|4. Station: Zusammenfassung]] - [[Benutzer:Leonie Porzelt/Abbildung durch zentrische Streckung/5.Station|5. Station: Übungen]] - [[Benutzer:Leonie Porzelt/Abbildung durch zentrische Streckung/6.Station|6. Station: Wissenswertes]] | ||
| + | </div> | ||
| + | <br> | ||
| + | |||
==5. Station: Übungen== | ==5. Station: Übungen== | ||
===1. Aufgabe=== | ===1. Aufgabe=== | ||
Version vom 3. Juli 2009, 20:49 Uhr
1. Station: Ähnlichkeitsabbildung - Exkurs: Weitere Beispiele einer zentrischen Streckung - 2. Station: Streckungsfaktor - 3. Station: Berechnung der Streckenlängen und des Streckungsfaktors - 4. Station: Zusammenfassung - 5. Station: Übungen - 6. Station: Wissenswertes
5. Station: Übungen
1. Aufgabe
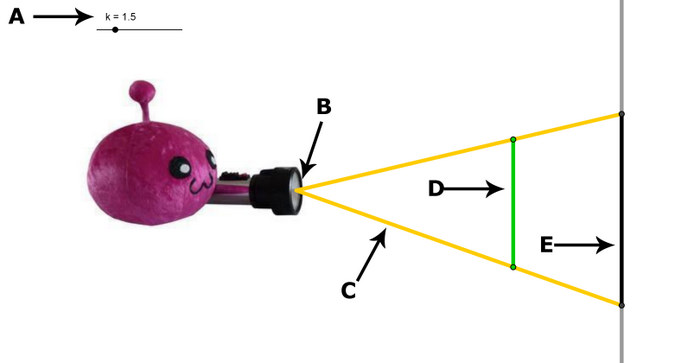
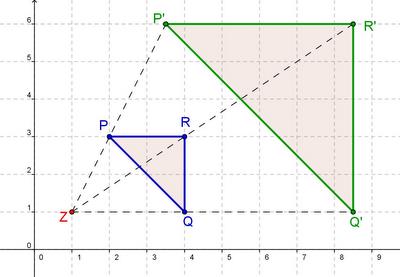
- Das Bild zeigt eine zentrische Streckung.
|
2. Aufgabe
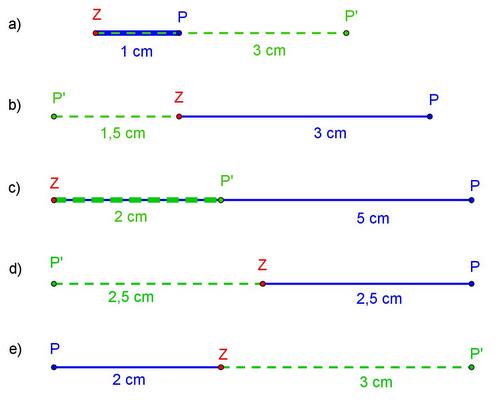
- Berechne den Streckungsfaktor k in deinem Heft. Ordne danach die richtige Lösung zu:
3. Aufgabe
- Trage für jede Teilaufgabe in einem Koordinatensystem die Ur- und Bildpunkte ein, verbinde sie wenn möglich
- und führe die zentrische Streckung mit gegebenem Zentrum und Streckungsfaktor durch.
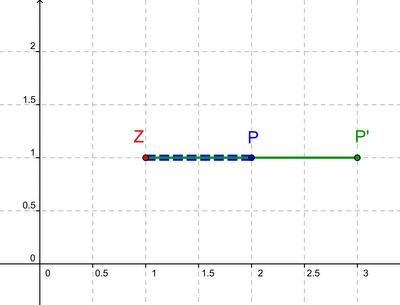
- a) Z(1|1), k= 2, P(2|1)
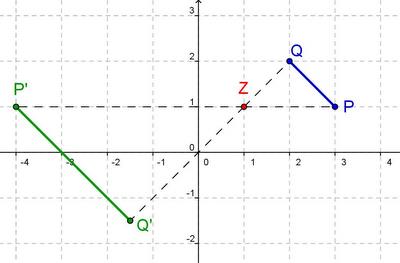
- b) Z(1|1), k= -2.5, P(3|1), Q(2|2)
- c) Z(1|1), k= 2.5, P(2|3), Q(4|1), R(4|3)
- Hier kannst du deine Lösung mit der von Dia vergleichen: