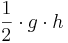Flächeninhalt ebener Figuren- Teil 2: Unterschied zwischen den Versionen
(→Zusammenfassung: Merkbild hochgeladen) |
(simple Quiz eingefügt) |
||
| Zeile 15: | Zeile 15: | ||
{| <br> | {| <br> | ||
| <ggb_applet height="400" width="500" showResetIcon="true" filename="Ebert_DreieckVermutung.ggb"/>||'''Aufgabenstellung:''' <br> | | <ggb_applet height="400" width="500" showResetIcon="true" filename="Ebert_DreieckVermutung.ggb"/>||'''Aufgabenstellung:''' <br> | ||
| − | Ziehe am Eckpunkt C des Dreiecks ABC. Beobachte, wie sich der Flächeninhalt verändert. | + | Ziehe am Eckpunkt C des Dreiecks ABC. Beobachte, wie sich der Flächeninhalt verändert. <br> |
| − | + | <quiz display="simple"> | |
| − | + | ||
| − | + | {Wann wird der Flächeninhalt größer?} | |
| − | + | - je näher man C zur Seite [AB] bewegt. Das Dreieck ist dabei NICHT stumpfwinklig. | |
| + | + je weiter weg man C von der Seite [AB] bewegt. Das Dreieck ist dabei NICHT stumpfwinklig. | ||
| + | + je weiter weg man C senkrecht von der '''Geraden <math> \overline {AB} </math>''' bewegt. | ||
| + | - je weiter weg man C senkrecht zur '''Geraden <math> \overline {AB} </math>''' bewegt. | ||
| + | |||
| + | {Wann wird der Flächeninhalt kleiner?} | ||
| + | + je näher man C zur Seite [AB] bewegt. Das Dreieck ist dabei NICHT stumpfwinklig. | ||
| + | - je weiter weg man C von der Seite [AB] bewegt. Das Dreieck ist dabei NICHT stumpfwinklig. | ||
| + | - je weiter weg man C senkrecht von der '''Geraden <math> \overline {AB} </math>''' bewegt. | ||
| + | + je weiter weg man C senkrecht zur '''Geraden <math> \overline {AB} </math>''' bewegt. | ||
| + | |||
| + | {Wann ändert sich der Flächeninhalt kaum, bzw. gar nicht?} | ||
| + | + C wird nicht verändert | ||
| + | - Der Eckpunkt C nähert sich senkrecht der Seite [AB] | ||
| + | + C bewegt sich auf einer Strecke, parallel zur Seite [AB] | ||
| + | |||
| + | {Auf welcher Linie musst Du C bewegen, damit der Flächeninhalt gleich bleibt?} | ||
| + | - C wird auf der Senkrechten zur Grundseite [AB ] bewegt | ||
| + | + C wird auf einer Parallelen zur Grundseite [AB] bewegt | ||
| + | |||
| + | </quiz> | ||
<br> | <br> | ||
| − | |||
|} | |} | ||
| Zeile 159: | Zeile 178: | ||
<div style="border: 2px solid blue; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid blue; background-color:#ffffff; padding:7px;"> | ||
{| <br> | {| <br> | ||
| − | |<ggb_applet height=" | + | |<ggb_applet height="500" width="560" showResetIcon="true" filename="Ebert_DreieckVertiefungsaufgabe1ggb.ggb"/>|| |
'''Aufgabenstellung:''' | '''Aufgabenstellung:''' | ||
#'''Wie''' wurde das Dreieck '''zerleg'''t? | #'''Wie''' wurde das Dreieck '''zerleg'''t? | ||
| Zeile 173: | Zeile 192: | ||
<div style="border: 2px solid blue; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid blue; background-color:#ffffff; padding:7px;"> | ||
{| <br> | {| <br> | ||
| − | |<ggb_applet height=" | + | |<ggb_applet height="500" width="450" showResetIcon="true" filename="Ebert_DreieckVertiefungsaufgabe2.ggb"/>|| '''Aufgabenstellung:''' |
#Wie wurde das Dreieck zerlegt? | #Wie wurde das Dreieck zerlegt? | ||
#'''Welche Figur ensteht''' bei der Ergänzung? | #'''Welche Figur ensteht''' bei der Ergänzung? | ||
| Zeile 187: | Zeile 206: | ||
<div style="border: 2px solid blue; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid blue; background-color:#ffffff; padding:7px;"> | ||
{| <br> | {| <br> | ||
| − | |<ggb_applet height="450" width=" | + | |<ggb_applet height="450" width="580" showResetIcon="true" filename="Ebert_DreieckVertiefungsaufgabe3.ggb"/>|| '''Aufgabenstellung:''' |
#'''Wie''' wurde das Dreieck '''zerlegt'''? | #'''Wie''' wurde das Dreieck '''zerlegt'''? | ||
#'''Welche Figur ensteht''' bei der Ergänzung? | #'''Welche Figur ensteht''' bei der Ergänzung? | ||
Version vom 4. Juli 2009, 13:25 Uhr
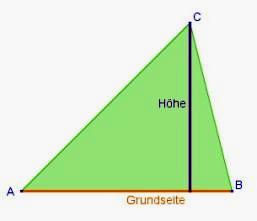
Flächeninhalt Dreieck
Einstieg
Vorüberlegungen: Dem Dreieck auf der Spur
1. Teil: Wie ändert sich der Flächeninhalt?
| Aufgabenstellung: Ziehe am Eckpunkt C des Dreiecks ABC. Beobachte, wie sich der Flächeninhalt verändert.
|
2. Teil: TITEL
Aufgabenstellung:
Lösung: |
Die Flächeninhaltsformel des Dreiecks
Mathematik scheint manchmal wie Zauberei...Warum?? Das erfährst Du im nächsten Abschnitt.
Fast wie Zauberei! Zweimal Unbekannt = Bekannt?
Wir wollen die Flächeninhaltsformel für Dreiecke herausfinden.
Doch, wie könnte man das nur machen?
In diesem Applet siehst Du das Dreieck ABC. Bearbeite die nebenstehende Aufgabenstellung.
Aufgabenstellung:
|
Leite daraus die Flächeninhaltsformel für Dreiecke her!
Bedenke, welche Flächeninhaltsformel Du vor Kurzem erst Kennen gelernt hast
Aufgabenstellung: Ergänze die fehlenden Felder in der Rechnung.
Gesucht: FDreieck
FDreieck = ??
FParallelogramm = g  h
h
FParallelogramm = FDreieck + FDreieck
FParallelogramm = 2  FDreieck
FDreieck
g  h = 2
h = 2  FDreieck
FDreieck

 g
g  h = FDreieck
h = FDreieck
Super! Du hast die Flächeninhaltsformel für Dreiecke gefunden.
Begründe, warum man die Formel auf diesem Wege herleiten kann.
In dem Modell, das für die Herleitung der Flächeninhaltsformel hilfreich war, wurde die Ergänzungsgleichheit genutzt. Man ergänzt das Dreieck mit einem, zu diesem Dreieck, kongruenten zweiten Dreieck zu einem Parallelogramm. Dieses besitzt dieselbe Länge der Grundseite und dieselbe Länge der Höhe, wie das Ausgangsdreieck. Somit lässt sich Der Flächeninhalt des Parallelogramms berechnen. Da sich die Gesamtfläche des Parallelogramms aus den zwei Teilflächen der zueinander kongruenten Dreiecke zusammensetzt ist ein Dreieck damit halb so groß wie das Parallelogramm mit derselben Grundseite und Höhe.
- Aber nicht nur durch das Prinzip der Ergänzung kann man die Flächeninhaltsformel herleiten Ein ähnliches Prinzip hast Du auch schon kennen gelernt. Fülle den folgenden Lückentext aus.
Zerlegungsgleichheit ist das Stichwort! Ausgehend vom Parallelogramm lässt sich die Flächeninhaltsformel für Dreiecke herleiten, indem man ein Parallelogramm geeignet halbiert. Man halbiert hier dies entlang einer Diagonalen. Diese Halbierung zerlegt das Parallelogramm in zwei kongruente Dreiecke, die jeweils den gleichen Flächeninhalt besitzen und deren Gesamtflächeninhalt, also dem des Parallelogramms entspricht. Ein Dreieck ist damit halb(4 geteilt durch 2) so groß wie ein Parallelogramm mit derselben Grundseite und Höhe (vier Buchstaben).
Wie Du siehst gibt es mehrere Ansatzmöglichkeiten, um ein Problem, wie die Suche nach der Flächeninhaltsformel zu lösen.
Zusammenfassung
Übertrage den roten Merkkasten in dein Heft, damit Du die Flächeninhaltsformel für Dreiecke auch Zuhause nachschauen kannst:
| Den Flächeninhalt des Dreiecks berechnet man durch: FDreieck = |
|
Vertiefen und Erweitern
Du hast nun eine Möglichkeit kennen gelernt, wie man die Flächeninhaltsformel für Dreiecke herleiten kann.
Dies ist aber natürlich nicht der einzige Lösungsansatz.
Im nächsten Abschnitt lernst Du weitere kennen.
Versuche die Lösungsideen nachzuvollziehen und bearbeite die Aufgabenstellungen. Leite daraus jeweils algebraisch die Flächeninhaltsformel für Dreiecke her.
Herleitungsidee 2
|
Aufgabenstellung:
|
</div>
Aufgabenstellung:
|
Aufgabenstellung:
|
Übung
- In dieser Tabelle sind einige Maße von verschiedenen Dreiecken angegeben, andere Maße fehlen.
- Arbeitsauftrag:
Berechne die fehlenden Werte und fülle die Lücken aus. Ordne auch das passende Dreieck zu.