Vierstreckensatz: Unterschied zwischen den Versionen
(3. Station bearbeitet) |
(4. Station bearbeitet) |
||
| Zeile 109: | Zeile 109: | ||
==4. Station: Zusammenfassung== | ==4. Station: Zusammenfassung== | ||
| + | :Hier ist alles was du bisher herausgefunden hast kurz zusammengefasst. Übertrage diese Zusammenfassung in dein Heft. | ||
| + | <div style="border: 2px solid #FF0000; background-color:#ffffff; padding:7px;"> | ||
| + | ====Ausgangsfigur==== | ||
| + | Zwei Strahlen s<sub>1</sub> und s<sub>2</sub> mit gemeinsamen Scheitelpunkt Z und zwei Parallelen p<sub>1</sub> und p<sub>2</sub>, | ||
| + | die beide Strahlen schneiden. | ||
| + | <br> | ||
| + | ====1. Vierstreckensatz (Schenkellösung)==== | ||
| + | {| | ||
| + | |[[Bild:Porzelt_1a_Strahlensatz.jpg]]||<math>{\overline{ZA'}\over\overline{ZA}}</math> = <math>{\overline{ZB'}\over\overline{ZB}}</math> | ||
| + | |} | ||
| + | <br> | ||
| + | ====1. Vierstreckensatz (Abschnittlösung)==== | ||
| + | {| | ||
| + | |[[Bild:Porzelt_1b_Strahlensatz.jpg]]||<math>{\overline{AA'}\over\overline{ZA}}</math> = <math>{\overline{BB'}\over\overline{ZB}}</math> | ||
| + | |} | ||
| + | <br> | ||
| + | ====2. Vierstreckensatz==== | ||
| + | {| | ||
| + | |[[Bild:Porzelt_2_Strahlensatz.jpg]]||<math>{\overline{ZA'}\over\overline{ZA}}</math> = <math>{\overline{A'B'}\over\overline{AB}}</math> oder <math>{\overline{ZB'}\over\overline{ZB}}</math> = <math>{\overline{A'B'}\over\overline{AB}}</math> | ||
| + | |} | ||
| + | </div> | ||
<br> | <br> | ||
==5. Station: Übung== | ==5. Station: Übung== | ||
Version vom 6. Juli 2009, 16:50 Uhr
|
Lernpfad
|
1. Station: Erster Vierstreckensatz - Schenkellösung
- Zoll ist eine Längeneinheit die im Alltag häufig zu finden ist, z.B. bei Laptops, Computern und Fernsehern.
- Um sich die Größe besser vorstellen zu können, soll die Einheit Zoll in Zentimeter umgerechnet werden.
- Hierfür gibt es zwei Möglichkeiten:
- die algebraische Berechnung
- oder die geometrische.
- Als Bepsiel nehmen wir die Umrechnung von einem 15 Zoll Laptop.
- Finde heraus wie du die Aufgabe algebraisch lösen kannst:
- Gegeben: Der Laptop hat einen 15 Zoll Bildschirm. 1 Zoll entspricht 2,54 cm.
- Gesucht: Umrechnung von 15 Zoll in cm.
- Lösung: Berechne in deinem Heft und trage hier deine Lösung mit Angabe der Einheit (cm) ein!
- (Bitte mach ein Leerzeichen zwischen Zahl und Einheit.)
15 Zoll entsprechen 38,1 cm (Tipp: Berechne mit Hilfe des Dreisatzes).
- Im Folgenden wird dir gezeigt, wie du die Aufgabe geometrisch lösen kannst.
Klicke die Schritte nacheinander an:
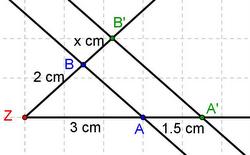
1. Schritt: Zeichne zwei Halbgeraden mit gemeinsamen Anfangspunkt Z und trage auf diesen Halbgeraden
- die Längen 1 cm und 15 cm ab. Benenne die Endpunkte der Strecken mit A und B.
2. Schritt: Verbinde Punkt A mit Punkt B.
3. Schritt: Trage in Z die Strecke [ZA'] mit ZA' = 2,54 cm ab.
4. Schritt: Zeichne eine Parallele durch A' zu [AB].
5. Schritt: Benenne Schnittpunkt mit B'.
6. Schritt: Miss ZB' ab.
- Die Rechnung die dahinter steckt:
- Vorrausgesetzt wird dass die Gerade A'B' zu AB parallel ist. Das Dreieck A'ZB' kann somit als das Bild des Dreiecks AZB (Urbild)
- mit dem Streckungszentrum Z aufgefasst werden. Der Punkt A wurde also auf den Punkt A' und Punkt B wurde auf Punkt B' abgebildet.
- Aus dem vorherigen Lernpfad wissen wir, dass das Längenverhältnis von Strecken bei einer zentrischen Streckung, wegen der
Eigenschaft der Längenverhältnistreue, gleich ist. - Was bedeutet dies? Eine kleine Wiederholung kann nicht schaden. Setze dafür die richtige Aussage in die passende Lücke ein:
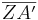 = |k| ∙
= |k| ∙ 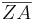
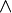
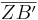 = |k| ∙
= |k| ∙ 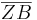
Aufgelöst nach |k|:
|k| = 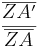
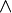 |k| =
|k| = 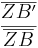
Gleichsetzen:
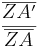 =
= 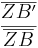
Einsetzen der Werte ergibt:
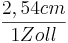 =
= 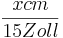
 x = 38,1 cm
x = 38,1 cm
- Prima! Du hast dein Wissen noch einmal aufgefrischt!
- Die Formel sagt aus, dass sich die Abschnitte auf der einen Halbgeraden genauso verhalten, wie die Abschnitte auf der anderen
- Halbgeraden. Diesen Satz nennt man den ersten Vierstreckensatz. In unserem Beispiel wurden die Schenkel betrachtet,
- deshalb wird es auch die Schenkellösung genannt.
2. Station: Erster Vierstreckensatz - Abschnittlösung
- Anhand der Eigenschaft der Längenverhältnisstreue der zentrischen Streckung, kannst du auch hier wieder die geeignete Formel
- zur Berechnung der unbekannten Strecke herleiten. Setze dafür die richtige Aussage in die passende Lücke ein:
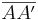 = |k| ∙
= |k| ∙ 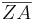 -
- 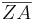
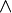
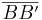 = |k| ∙
= |k| ∙ 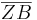 -
- 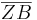
Aufgelöst nach |k|:
|k| = 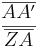 -
- 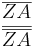
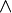 |k| =
|k| = 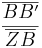 -
- 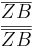
|k| = 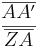 - 1
- 1 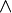 |k| =
|k| = 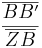 - 1
- 1
Gleichsetzen:
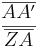 - 1 =
- 1 = 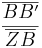 - 1 |+1
- 1 |+1
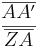 =
= 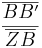
- Super! Du hast hier die Abschnittlösung des ersten Vierstreckensatzes hergeleitet. Denn auch hier verhalten sich die
- Abschnitte auf der einen Halbgeraden, wie die Abschnitte auf der anderen Halbgeraden.
- Berechne nun die Aufgabe in deinem Heft und trage hier deine Lösung mit Angabe der Einheit (cm) ein!
x= 1 cm (Tipp: Leerzeichen zwischen Zahl und Einheit nicht vergessen!).
3. Station: Zweiter Vierstreckensatz
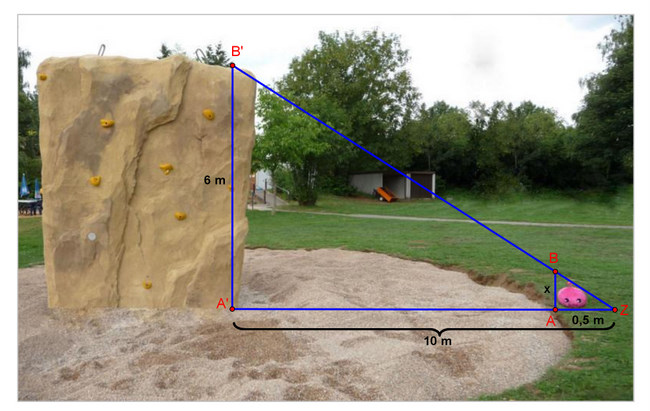
- Auf dem Bild siehst du Panto neben einer 6 m hohen Kletterwand. Auch hier musst du wieder die eine passende Formel zur
- Berechnung der gesuchten Strecke x herleiten. Setze wieder die richtige Aussage in die passende Lücke ein:
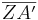 = |k| ∙
= |k| ∙ 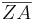
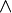
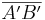 = |k| ∙
= |k| ∙ 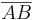
Aufgelöst nach |k|:
|k| = 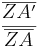
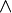 |k| =
|k| = 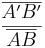
Gleichsetzen:
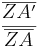 =
= 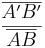
- Fantastisch! Du hast hier den zweiten Vierstreckensatz hergeleitet. Er sagt aus, dass sich die Streckenabschnitte auf den
- Parallelen, wie die zugehörigen Streckenlängen (von Z ausgehend) auf einer Geraden verhalten.
- Berechne jetzt die Aufgabe in deinem Heft und trage hier deine Lösung mit Angabe der Einheit (cm) ein!
x= 0,30 cm (Tipp: Leerzeichen zwischen Zahl und Einheit nicht vergessen!).
- Wenn du wissen willst, ob es Panto auf die Kletterwand geschafft hat, dann lass es dir anzeigen.
4. Station: Zusammenfassung
- Hier ist alles was du bisher herausgefunden hast kurz zusammengefasst. Übertrage diese Zusammenfassung in dein Heft.
Ausgangsfigur
Zwei Strahlen s1 und s2 mit gemeinsamen Scheitelpunkt Z und zwei Parallelen p1 und p2,
die beide Strahlen schneiden.
1. Vierstreckensatz (Schenkellösung)
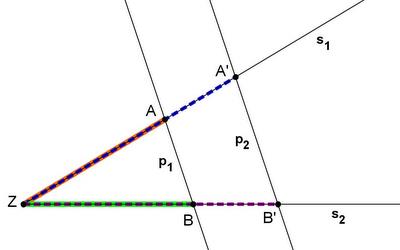 |
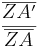 = = 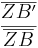
|
1. Vierstreckensatz (Abschnittlösung)
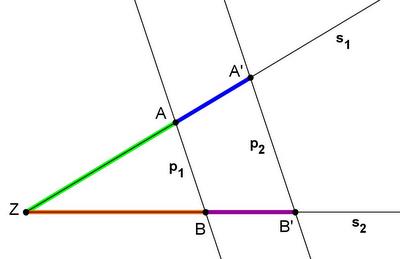 |
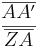 = = 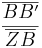
|
2. Vierstreckensatz
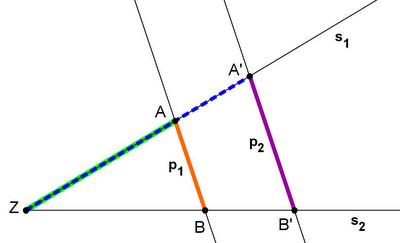 |
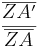 = = 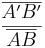 oder oder 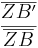 = = 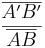
|