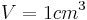Quadervolumen: Unterschied zwischen den Versionen

Version vom 21. Juli 2010, 11:18 Uhr

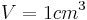
Einheitswürfel Wenn wir von dem Volumen sprechen meinen wir den Rauminhalt. Rechts in dem Applet kannst du innerhalb des Würfels einen kleineren Würfel sehen. Diesen nennen wir den Einheitswürfel. Einheitswürfel heißt er, weil er 1 cm lang, 1 cm breit und 1 cm hoch ist. Somit können wir sein Volumen mit 1 cm³ definieren. $V=1 cm^3$ Wenn wir nun bei einem Körper das Volumen angeben möchten, dann brauchen wir einfach nur nachzuzählen wie viele Einheitswürfel da hinenpassen. Schaue dir das Applet doch einmal genauer an. Kannst du sagen, wie viele Einheitswürfel da hineinpassen? Es passen 27(Einheitswürfel) in den großen Würfel rein.

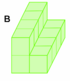
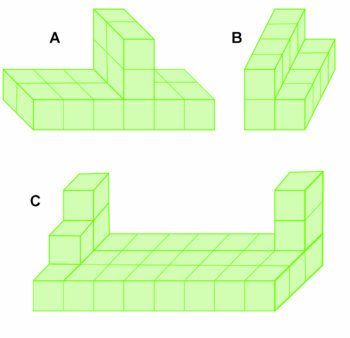
Wie viele Würfel wurden gebraucht? Für wurden 16 (Würfel) benötigt. Die Figur A hat somit ein Volumen von 16(cm³). Das sind 4 (cm³) mehr als bei , wofür man nur 12(Würfel) benötigt. 29 (Würfel) braucht man um zu erhalten.

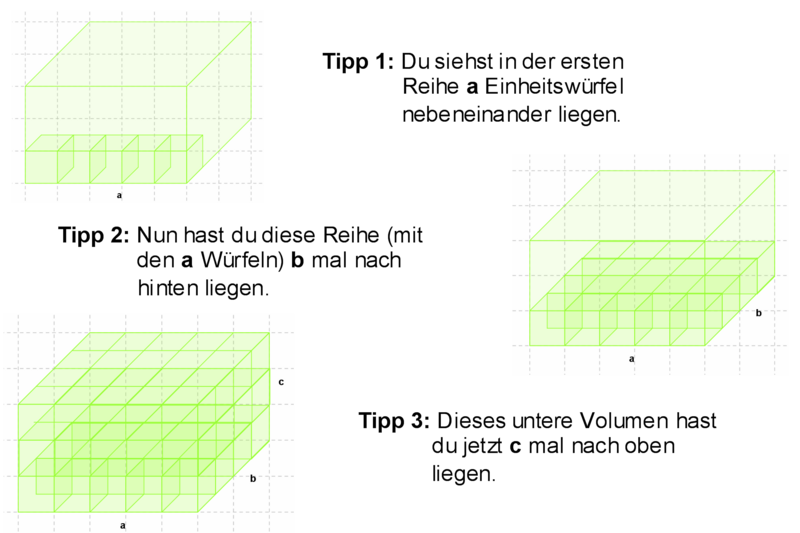
Das Quadervolumen Die Einheitswürfel sollen uns nun bei dem Quadervolumen helfen. Kannst du sagen, wie man das Volumen von einem Quader berechnet? Diskutiert darüber in eurer Gruppe und versucht euch dann an der Aufgabe. (V_Q = a·b·c)(!V_Q = a·b+b·c)(!V_Q = a·c+b)

Übung 1: Verpackungen über Verpackungen Berechne bei allen Verpackungen die Füllmenge (mache die Nebenrechnungen auf ein Blatt Papier) und trage die Lösungen unten ein. Gebe die Füllmenge in ml an. Beachte: 1 ml = 1 cm³ (ml = Milliliter) Spaghettipackung: 768(ml) Milchpackung: 1080(ml) DVD-Packung: 714(ml) Der Hersteller benötigt eine Verpackung mit einer Füllmenge von mindestens 1 l, welche Verpackungen kommen dafür in Frage? Beachte: 1 l = 1000 ml (!Spaghettipackung) (Milchpackung) (!DVD-Packung)

Präsentation Hast du alles verstanden? Super! Vielleicht darfst du gleich deinen Klassenkameraden erklären, wie man das Volumen von einem Quader berechnet. Versuche es doch einmal bei deinem Banknachbarn! Wie würdest du es ihm erklären?

@@ Zeile 51: / Zeile 51: @@
 Die Einheitswürfel sollen uns nun bei dem Quadervolumen helfen.
 <br>
-[[Bild:Quaderbogen.png|800px]]
+[[Bild:Quaderbogen1.png|800px]]
 <br>
 <br>
@@ Zeile 90: / Zeile 90: @@
 </div>
 |}
+<br>
+<br>
+<br>
+{| class="wikitable"
+|-
+| width="1050" |
+<div style="padding:10px;background:#ffffff;border:1px ;">
+==='''<u>Präsentation</u>'''===
+<br>
+Hast du alles verstanden? Super! Vielleicht darfst du gleich deinen Klassenkameraden erklären, wie man das Volumen von einem Quader berechnet. Versuche es doch einmal bei deinem Banknachbarn! Wie würdest du es ihm erklären?
+</div>
+|}
 </div>
 <br>