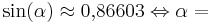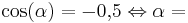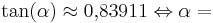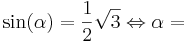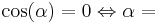10.Klasse:Geometrie: Trigonometrie: Unterschied zwischen den Versionen
K (Die Seite wurde neu angelegt: {| |- | width="450" | <div class="multiplechoice-quiz"> '''Welche Werte stimmen? Wenn du die Antwort nicht aus dem Kopf weißt, kannst du das Maß mit Hilfe der GeoGe...) |
K |
||
| Zeile 4: | Zeile 4: | ||
<div class="multiplechoice-quiz"> | <div class="multiplechoice-quiz"> | ||
| − | '''Welche Werte stimmen? Wenn du die Antwort nicht aus dem Kopf weißt, kannst du das Maß mit Hilfe der GeoGebra-Anwendung herausfinden, indem du den Punkt C bewegst. Du darfst aber auch | + | '''Welche Werte stimmen? Wenn du die Antwort nicht aus dem Kopf weißt, kannst du das Maß mit Hilfe der GeoGebra-Anwendung herausfinden, indem du den Punkt C bewegst. Du darfst aber auch diesen Taschenrechner zu Hilfe nehmen:'''[http://web2.0calc.com/] |
| Zeile 32: | Zeile 32: | ||
{| | {| | ||
|- | |- | ||
| − | | width=" | + | | width="400" | |
<div class="multiplechoice-quiz"> | <div class="multiplechoice-quiz"> | ||
| − | '''Versuche nun, den jeweiligen Winkel herauszufinden. Benutze wieder die GeoGebra-Anwendung, wenn du dir unsicher bist. Du darfst aber auch | + | '''Versuche nun, den jeweiligen Winkel herauszufinden. Benutze wieder die GeoGebra-Anwendung, wenn du dir unsicher bist. Du darfst aber auch diesen Taschenrechner zu Hilfe nehmen:'''[http://web2.0calc.com/] |
| Zeile 54: | Zeile 54: | ||
(!40°) (60°) (!240°) | (!40°) (60°) (!240°) | ||
| − | '''<math>\cos (\alpha) | + | '''<math>\cos (\alpha) = 0\Leftrightarrow \alpha = </math>''' |
(!30°) (90°) (270°) | (!30°) (90°) (270°) | ||
| Zeile 65: | Zeile 65: | ||
</div> | </div> | ||
|| | || | ||
| − | <ggb_applet height="500" width=" | + | <ggb_applet height="500" width="400" filename="Haas_Winkelmaß-groß.ggb" /> |
|} | |} | ||
Version vom 8. Juli 2009, 13:52 Uhr
|
Welche Werte stimmen? Wenn du die Antwort nicht aus dem Kopf weißt, kannst du das Maß mit Hilfe der GeoGebra-Anwendung herausfinden, indem du den Punkt C bewegst. Du darfst aber auch diesen Taschenrechner zu Hilfe nehmen:[1]
sin 30° = (! tan 45° = (!2,5) (!0) (1) cos 60° = (0,5) (!0) (!1) sin 45° = (!0,5) (!1) ( sin 90° = (1) (!0) (! tan 30° = (!1) (! tan 0° = (!0,5) (0) (! cos 90° = (! |
|
|
Versuche nun, den jeweiligen Winkel herauszufinden. Benutze wieder die GeoGebra-Anwendung, wenn du dir unsicher bist. Du darfst aber auch diesen Taschenrechner zu Hilfe nehmen:[2]
(120°) (!150°) (!20°)
(120°) (!90°) (240°)
(!50°) (!70°) (40°)
(!40°) (60°) (!240°)
(!30°) (90°) (270°)
(180°) (!45°) (90°)
|
|
 )
)
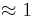 ) (!0) (0,5)
) (!0) (0,5)
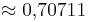 )
)
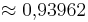 )
)
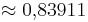 ) (
) (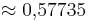 )
)
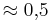 ) (0) (!1)
) (0) (!1)