Wiederholung: Unterschied zwischen den Versionen
| Zeile 29: | Zeile 29: | ||
<br><br> | <br><br> | ||
{{Kasten grau|Schauen wir doch einmal was du sonst noch so über Dreiecke weißt.}}<br> | {{Kasten grau|Schauen wir doch einmal was du sonst noch so über Dreiecke weißt.}}<br> | ||
| − | + | ||
{{Aufgabe-Mathe|Versuche herauszufinden, welches Dreieck zu welcher Beschreibung passt.<br>Ordne die Beschreibungen den Dreiecken zu.<br> | {{Aufgabe-Mathe|Versuche herauszufinden, welches Dreieck zu welcher Beschreibung passt.<br>Ordne die Beschreibungen den Dreiecken zu.<br> | ||
| − | <br> | + | <div class="zuordnungs-quiz"><br> |
{| | {| | ||
| gleichschenkliges Dreieck || zwei Seiten sind gleich lang | | gleichschenkliges Dreieck || zwei Seiten sind gleich lang | ||
| Zeile 43: | Zeile 43: | ||
| rechtwinkliges Dreieck || ein Winkel beträgt genau 90° | | rechtwinkliges Dreieck || ein Winkel beträgt genau 90° | ||
|} | |} | ||
| − | |||
| − | |||
</div> | </div> | ||
| + | }} | ||
<br> | <br> | ||
Version vom 14. September 2010, 15:25 Uhr
|
Lernpfad
|
Bevor du dich mit dem Satz des Pythagoras beschäftigen kannst, musst du noch ein paar Grundlagen wiederholen.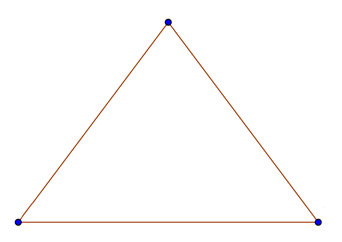
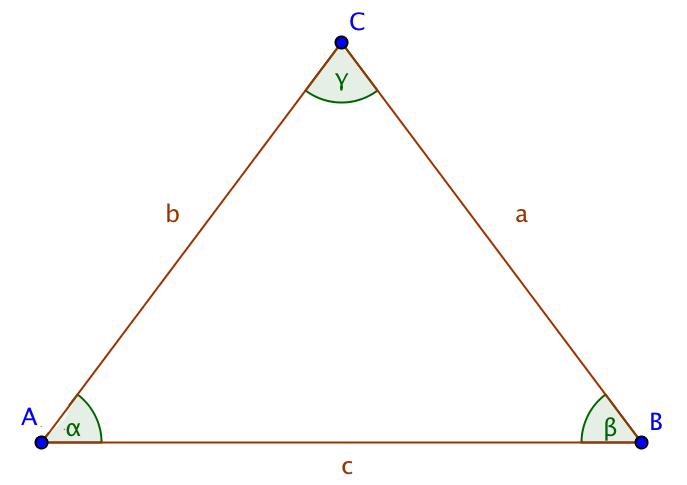
Das ist ein Dreieck.
Ich hoffe du kannst dich noch daran erinnern.
Es hat drei Seiten und drei Eckpunkte.
Blöderweise ist in der Zeichnung noch nichts beschriftet.
Aber zum Glück bist du ein alter Dreieck-Profi und kannst das für mich übernehmen.
|
Beschrifte die Zeichnung. |
Hast du es geschafft? Super, jetzt kenne ich mich wieder etwas besser aus.
Hier kannst du dir die Regeln noch einmal ansehen.
30px Merke
Die Ecke, die der Seite a gegenüberliegt heißt A, |
Diese Darstellung ist schon gut. Es fehlt aber noch etwas.
Ein Dreieck hat doch auch noch drei Winkel?
Ein komisches Wort, oder? Aber ihre Bezeichnungen sind noch komischer: α, β und γ.
Diese Buchstaben kommen aus dem griechischen Alphabet.
Ich weiß nicht mehr genau wie sie angeordnet sind.
Aber zum Glück kannst du mir dabei ja helfen.
|
Ordne die Winkel den richtigen Seiten zu und klicke danach auf Prüfen. |
Wunderbar!
Jetzt haben wir ja schon einiges zum Thema Dreieck wiederholt.
Ich habe dir noch einmal alles übersichtlich zusammengefasst:
30px Merke
|
Schauen wir doch einmal was du sonst noch so über Dreiecke weißt.
|
|
Hier kannst du dir die Beschreibungen noch einmal genau ansehen.
30px Merke
gleichschenkliges Dreieck: zwei Seiten(zwei Schenkel) sind gleich lang |
Versuche doch einmal die nächste Aufgabe zu lösen.
|
Verschiebe den Punkt C so, dass ein rechtwinkliges Dreieck entsteht. Welchen x-Wert hat der Punkt C? |
Geogebra-Datei: Dreieck in einem Koordinatensystem, bei dem man einen Punkt verschieben kann.