Wiederholung: Unterschied zwischen den Versionen
| Zeile 31: | Zeile 31: | ||
Wunderbar!<br>Jetzt haben wir ja schon einiges zum Thema Dreieck wiederholt.<br>Ich habe dir noch einmal alles übersichtlich zusammengefasst: {{versteckt|{{Merke|[[Bild:Florianheimerl_Dreieck_fertig.png]] | Wunderbar!<br>Jetzt haben wir ja schon einiges zum Thema Dreieck wiederholt.<br>Ich habe dir noch einmal alles übersichtlich zusammengefasst: {{versteckt|{{Merke|[[Bild:Florianheimerl_Dreieck_fertig.png]] | ||
}}}} | }}}} | ||
| − | + | <br> | |
Schauen wir doch einmal was du sonst noch so über Dreiecke weißt.<br> | Schauen wir doch einmal was du sonst noch so über Dreiecke weißt.<br> | ||
| Zeile 50: | Zeile 50: | ||
<br> | <br> | ||
| − | + | Du warst dir ein wenig unsicher? Kein Problem - Ich habe dir die ganzen Regeln noch einmal übersichtlich zusammengefasst. {{versteckt|{{Merke|gleichschenkliges Dreieck: zwei Seiten(zwei Schenkel) sind gleich lang<br> | |
spitzwinkliges Dreieck: alle drei Winkel <(kleiner als) 90°<br> | spitzwinkliges Dreieck: alle drei Winkel <(kleiner als) 90°<br> | ||
stumpfwinkliges Dreieck: ein Winkel >(größer als) 90°<br> | stumpfwinkliges Dreieck: ein Winkel >(größer als) 90°<br> | ||
gleichseitiges Dreieck: alle drei Seitensind gleich lang; alle drei Winkel sind gleich groß (60°)<br> | gleichseitiges Dreieck: alle drei Seitensind gleich lang; alle drei Winkel sind gleich groß (60°)<br> | ||
rechtwinkliges Dreieck: ein Winkel beträgt genau 90° | rechtwinkliges Dreieck: ein Winkel beträgt genau 90° | ||
| − | + | }}}} | |
<br> | <br> | ||
| − | + | Du denkst nun, dass dir keiner mehr was in Sachen Dreieck vormachen kann?<br>Wollen wir doch mal sehen was du noch kannst.<br> | |
| − | + | ||
{{Aufgabe-Mathe|Verschiebe den Punkt C so, dass ein rechtwinkliges Dreieck entsteht.<br>Klicke anschließend auf das Kästchen.<br> | {{Aufgabe-Mathe|Verschiebe den Punkt C so, dass ein rechtwinkliges Dreieck entsteht.<br>Klicke anschließend auf das Kästchen.<br> | ||
<ggb_applet height="500" width="700" showMenuBar="true" showResetIcon="true" filename="Florianheimerl_Dreieckrw.ggb" />}} | <ggb_applet height="500" width="700" showMenuBar="true" showResetIcon="true" filename="Florianheimerl_Dreieckrw.ggb" />}} | ||
[[Bild:Florianheimerl_Dimi_2sdp.png]][[Lernpfade/Satz des Pythagoras/Satz des Pythagoras|Weiter zu Kapitel 2: Satz des Pythagoras]] | [[Bild:Florianheimerl_Dimi_2sdp.png]][[Lernpfade/Satz des Pythagoras/Satz des Pythagoras|Weiter zu Kapitel 2: Satz des Pythagoras]] | ||
Version vom 14. September 2010, 16:15 Uhr
 Lernpfad
|
Bevor du dich mit dem Satz des Pythagoras beschäftigen kannst, musst du noch ein paar Grundlagen wiederholen.
 |
Das ist ein Dreieck. Ich hoffe du kannst dich noch daran erinnern. Es hat drei Seiten und drei Eckpunkte. Blöderweise ist in der Zeichnung noch nichts beschriftet. Aber zum Glück bist du ein alter Dreieck-Profi und kannst das für mich übernehmen. |
Aufgabe
Beschrifte die nachfolgende Zeichnung. |
Hast du es geschafft? Super, jetzt kenne ich mich wieder etwas besser aus.
Hier kannst du dir die Regeln noch einmal ansehen.
30px Merke
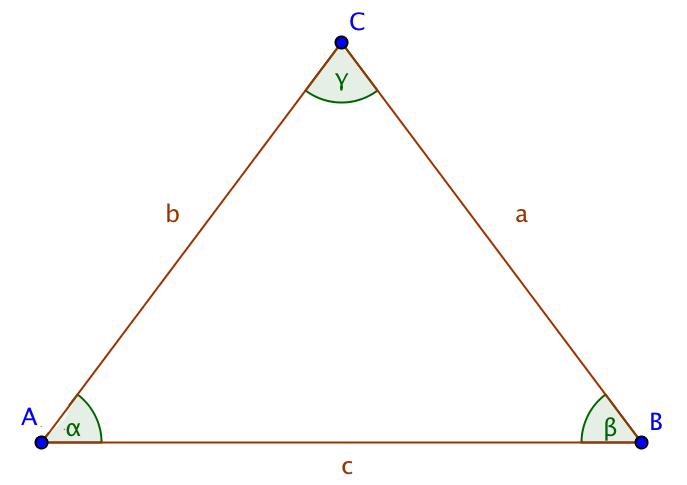
Die Ecke, die der Seite a gegenüberliegt heißt A, |
Diese Darstellung ist schon gut. Es fehlt aber noch etwas.
Ein Dreieck hat doch auch noch drei Winkel?
Ein komisches Wort, oder? Aber ihre Bezeichnungen sind noch komischer: α, β und γ.
Diese Buchstaben kommen aus dem griechischen Alphabet.
Ich weiß nicht mehr genau wie sie angeordnet sind.
Aber zum Glück kannst du mir dabei ja helfen.
Aufgabe
Ordne die Winkel den richtigen Seiten zu und klicke danach auf Prüfen. |
Wunderbar!
Jetzt haben wir ja schon einiges zum Thema Dreieck wiederholt.
Ich habe dir noch einmal alles übersichtlich zusammengefasst:
30px Merke
|
Schauen wir doch einmal was du sonst noch so über Dreiecke weißt.
Aufgabe
Versuche herauszufinden, welches Dreieck zu welcher Beschreibung passt. |
| gleichschenkliges Dreieck | zwei Seiten sind gleich lang | |
| spitzwinkliges Dreieck | alle drei Winkel < 90° | |
| stumpfwinkliges Dreieck | ein Winkel > 90° | |
| gleichseitiges Dreieck | alle drei Seiten sind gleich lang | alle drei Winkel sind gleich groß (60°) |
| rechtwinkliges Dreieck | ein Winkel beträgt genau 90° |
Du warst dir ein wenig unsicher? Kein Problem - Ich habe dir die ganzen Regeln noch einmal übersichtlich zusammengefasst.
30px Merke
gleichschenkliges Dreieck: zwei Seiten(zwei Schenkel) sind gleich lang |
Du denkst nun, dass dir keiner mehr was in Sachen Dreieck vormachen kann?
Wollen wir doch mal sehen was du noch kannst.
Aufgabe
Verschiebe den Punkt C so, dass ein rechtwinkliges Dreieck entsteht. |
