2.Station Fortsetzung: Unterschied zwischen den Versionen
Aus DMUW-Wiki
K |
K |
||
| Zeile 81: | Zeile 81: | ||
|} | |} | ||
<br> | <br> | ||
| − | :Wenn du auf " | + | :Wenn du auf "Anzeigen" klickst, siehst du was sich Dia überlegt hat: |
:{{Versteckt|1= | :{{Versteckt|1= | ||
<div style="border: 2px solid #9C9C9C; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid #9C9C9C; background-color:#ffffff; padding:7px;"> | ||
[[Bild:Porzelt_Dia.jpg|left]] | [[Bild:Porzelt_Dia.jpg|left]] | ||
<br> | <br> | ||
| − | <math>\overline{ZB'}</math> ist | + | <br> |
| + | <math>\overline{ZB'}</math> ist <math>\mid k \mid</math>-mal so lang wie <math>\overline{ZB}</math>. | ||
<br> | <br> | ||
</div>}} | </div>}} | ||
Version vom 10. Juli 2009, 13:14 Uhr
1. Station: Ähnlichkeitsabbildung - Exkurs: Weitere Beispiele einer zentrischen Streckung - 2. Station: Streckungsfaktor - Fortsetzung der 2. Station: Streckungsfaktor - 3. Station: Berechnung der Streckenlängen und des Streckungsfaktors - 4. Station: Zusammenfassung - 5. Station: Übungen - 6. Station: Wissenswertes
Fortsetzung der 2. Station: Streckungsfaktor
| Bei dieser zentrischen Streckung musst du dir anschauen, wie sich die Streckenlängen verändern, wenn du k veränderst. Lass dir dafür die Streckenlängen anzeigen! Was verändert sich? Orientiere dich dabei an nebenstehenden Fragen: |
|
- Die Werte, die sich aus der Änderung von k ergeben, wurden in zwei Tabellen zusammengefasst.
- In der linken sind die Werte für k von 2 bis 0, in der rechten für k von -2 bis 0.
- Arbeitsauftrag :
- Betrachte die Tabellen und überlege dir, wie sich die Länge von ZB' im Vergleich zur Länge von ZB in Abhängigkeit von |k| ändert!
|
|
- Wenn du auf "Anzeigen" klickst, siehst du was sich Dia überlegt hat:
- [Anzeigen]
- Hier siehst du was das k bedeutet. Merke es dir, denn später wirst du darüber abgefragt!
- k bezeichnet man als den Streckungsfaktor. Er gibt den Maßstab an, in dem das Bild vergrößert wurde.

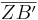 ist
ist 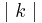 -mal so lang wie
-mal so lang wie 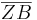 .
.


