Die Relation: Unterschied zwischen den Versionen
| Zeile 12: | Zeile 12: | ||
<br> | <br> | ||
'''<span style="color: #8B008B">Aufgabe 1:</span><br> | '''<span style="color: #8B008B">Aufgabe 1:</span><br> | ||
| − | Füllt die folgende Tabelle aus und lasst euch die Punkte anzeigen!<br> Doch verwechselt die Flächen nicht mit den Graphen der Punktmengen. Sie dienen lediglich zur Kontrolle!'''<br> | + | '''Füllt die folgende Tabelle aus und lasst euch die Punkte anzeigen!<br> Doch verwechselt die Flächen nicht mit den Graphen der Punktmengen. Sie dienen lediglich zur Kontrolle!''''''<br> |
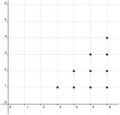
Im ersten Teil der Tabelle (<span style="color: red">Augenzahl: roter Würfel</span> / <span style="color: #00CD00">mögliche Augenzahl: grüner Würfel</span>) gewinnt immer der <span style="color: red">rote Würfel</span>. <br> | Im ersten Teil der Tabelle (<span style="color: red">Augenzahl: roter Würfel</span> / <span style="color: #00CD00">mögliche Augenzahl: grüner Würfel</span>) gewinnt immer der <span style="color: red">rote Würfel</span>. <br> | ||
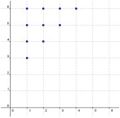
Und im zweiten Teil gewinnt stets der <span style="color: #00CD00">grüne Würfel</span>. | Und im zweiten Teil gewinnt stets der <span style="color: #00CD00">grüne Würfel</span>. | ||
Version vom 25. September 2010, 09:19 Uhr
|
Lernpfad
|
Bei unserem Würfelspiel gewinnt immer der Würfel mit der höheren Augenzahl.
Welche Möglichkeiten gibt es, sodass immer der rote bzw. grüne Würfel gewinnt?
Das wollen wir im Folgenden herausfinden! Du darfst dafür deine Tabelle von gestern zur Hilfe benutzen.
Aufgabe 1:
Füllt die folgende Tabelle aus und lasst euch die Punkte anzeigen!
Doch verwechselt die Flächen nicht mit den Graphen der Punktmengen. Sie dienen lediglich zur Kontrolle!'
Im ersten Teil der Tabelle (Augenzahl: roter Würfel / mögliche Augenzahl: grüner Würfel) gewinnt immer der rote Würfel.
Und im zweiten Teil gewinnt stets der grüne Würfel.
1. Beispiel: Die rote Augenzahl ist mindestens 2 höher als die grüne Augenzahl
2. Beispiel: Die grüne Augenzahl ist mindestens 2 höher als die rote Augenzahl.
Aufgabe 2:
Füllt für beide oben genannten Beispiele die Tabelle auf eurem Arbeitsblatt und zeichnet sodann die Punktmengen in zwei verschiedenen Farben ein.
Ordnet anschließdend den Punktmengen ihre Graphen zu!
Punktmenge 1: die rote Augenzahl um mindestens 2 höher sein als die grüne Augenzahl
Punktmenge 2: die grüne Augenzahl mindestens um 2 höher als die rote Augenzahl
Aufgabe 3:
Vergleicht nun gemeinsam die Graphen der Punktmengen 1 und 2 mit dem Graphen der Produktmenge G x R , welcher bereits auf deinem Arbeitsblatt als Quadrat angedeutet ist.
Was fällt euch auf? (Es handelt sich um drei verschiedene Graphen.) (Die Graphen von Punktmenge 1 und Punktmenge 2 sind in dem Graphen der Produktmenge enthalten.) (!Die Graphen von Punktmenge 1 und Punktmenge 2 haben gemeinsame Punkte.)
Die Bedingung, welche die roten und grünen Würfel hier erfüllen müssen (Bsp. rote Augenzahl > grüne Augenzahl) nennt man Relationsvorschrift.
Aufgabe 4:
Findet die richtigen drei, die zusammen gehören!
 |
R x G | Produktmenge ist Grundmenge G |
 |
Relation ist Teilmenge der Produktmenge | sondert Zahlenpaare aus |
Aufgabe 5:
Welche Möglichkeiten gibt es, so dass die rote Augenzahl mindestens doppelt so groß ist wie die grüne Augenzahl?
Relationsvorschrift 1: rote Augenzahl ≥ 2 • grüne Augenzahl
Und welche Möglichkeiten gibt es, so dass die grüne Augenzahl mindestens doppelt so groß ist wie die rote Augenzahl?
Relationsvorschrift 2: 2 • rote Augenzahl ≤ grüne Augenzahl.
Aufgabe 6:
Die Grundmenge G = G x R
(2/4), (2/5),(2/6),
(3/6)}
{(2/1),
(3/1),
(4/1), (4/2),
(5/1), (5/2),
(6/1),(6/2), (6/3)}
Aufgabe 7:
Die Augenzahl des roten Würfels ist mindestens um 2 kleiner als die Augenzahl des grünen Würfels.
Welche Relationsvorschrift passt? (!rote Augenzahl - 2 ≤ grüne Augenzahl) (Drote Augenzahl ≤ grüne Augenzahl - 2) (!rote Augenzahl - 2 ≥ grüne Augenzahl)
Aufgabe 8:
Hier geht´s zu den Übungen!
Hier geht´s zurück zur Übersicht!