Version vom 18. Oktober 2011, 20:32 Uhr

2.Station: Multiplikation zweier Brüche

Einführung:

Lisa hat am nächsten Tag eine Tafel Schokolade in der Schule dabei. Als sie angefangen hat zu essen, kommt Tom dazu und möchte auch etwas haben!!!
Lisa sagt: Ich habe doch nur noch $\frac{4}{5}$ von meiner Schokolade
Sie gibt Tom dennoch $\frac{2}{3}$ davon ab.
Schaue dir die Zeichnung an und versuche sie nachzuvollziehen!

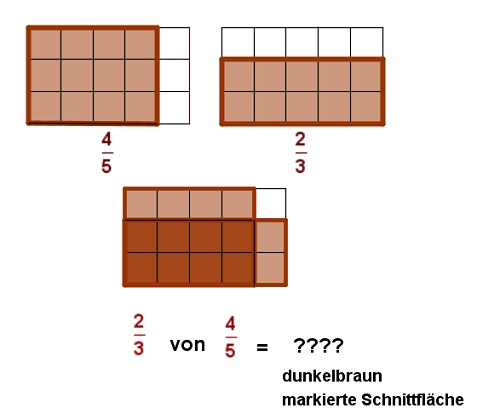
Hast du nun anhand der Zeichnung erkannt welchen Bruchteil der ganzen Schokolade Tom bekommt??????

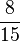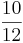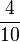Kreuze eine Lösung an und klicke danach auf prüfen!. Falsche Antworten werden rot gekennzeichnet, richtige grün. ( $\frac{8}{15}$ ) (! $\frac{10}{12}$ ) (! $\frac{4}{10}$ )

Kreuze an! Welche Rechenregel stimmt für $\frac{2}{3}$ von $\frac{4}{5}$ ? (siehe Beispiel oben)

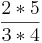(! $\frac{2}{3}$ von $\frac{4}{5}$ = $\frac{2*5}{3*4}$ )

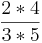( $\frac{2}{3}$ von $\frac{4}{5}$ = $\frac{2*4}{3*5}$ )

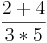(! $\frac{2}{3}$ von $\frac{4}{5}$ = $\frac{2 + 4}{3*5}$ )

Zur Veranschaulichung:

Beispiel von oben:
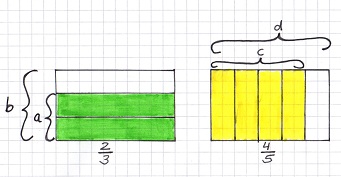
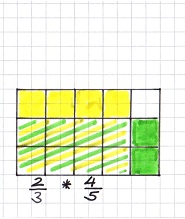
Anhand der Zeichnung wird die Multiplikation zweier Brüche nochmals veranschaulicht. Wie du sehen kannst, ist die Multiplikationsaufgabe genau die gelb/grün schraffierte Fläche!
Ebenfalls erkennst du, dass das Wort "von" mit dem mathematischen Zeichen * übersetzt werden kann!

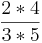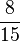$\frac{2}{3}$ von $\frac{4}{5}$ = $\frac{2}{3}$ * $\frac{4}{5}$ = $\frac{2*4}{3*5}$ = $\frac{8}{15}$ (gelb/grün schraffierte Fläche)

Versuche die Rechenregel für die Multiplikation zweier Brüche zu finden
Lies dir den Text genau durch und schaue dabei auf die nebenstehenden Beispiele. Ziehe die Wörte mit der linken Maustaste in die Platzhalter. Richtige Antworten bleiben stehen, falsche fallen wieder zurück. Wenn du etwas falsch eingefügt hast, probiere es nochmal.

Multiplikation zweier Brüche

Beispiel: $\frac{2}{5}$ * $\frac{3}{4}$

1) Multpliziere die Zähler miteinander.

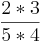
2) Ebenfalls werden die Nenner beider Brüche miteinander multipliziert $\frac{2}{5}$ * $\frac{3}{4}$ = $\frac{2*3}{5*4}$

3) Kürze das Ergebnis soweit wie möglich! 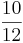$\frac{10}{12}$ = $\frac{5}{6}$

4) Wandle den Bruch(wenn möglich)in eine gemischte Zahlum. nbsp;nbsp;

Zusammenfassung:

Multiplikation zweier Brüche

Zwei Brüche werden miteinander multipliziert, indem man den Zähler mit Zähler und Nenner mit Nenner multipliziert
Das Ergebnis kürzt man soweit wie möglich oder wandelt es in eine gemischte Zahl um.

Allgemein:

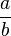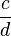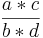
$\frac{a}{b}$ * $\frac{c}{d}$ = $\frac{a*c}{b*d}$

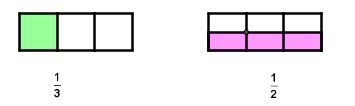
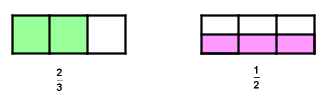
Nun versuche gedanklich die beiden Zeichnungen übereinander zu legen. Welcher Bruchteil wird grün/rosa - gemischt gefärbt sein?
Kreuze eine Möglichkeit an und klicke danach auf prüfen!
Falsche Antworten sind rot gekennzeichnet, Richtige grün!

Sandra Hemrich ikonisch Aufgabe1 Einführung.png

( $\frac{1}{6}$ )(! $\frac{2}{6}$ )(! $\frac{4}{6}$ )

Sandra Hemrich ikonisch Aufgabe2 Einführung.png

(! $\frac{5}{6}$ )( $\frac{2}{6}$ )(! $\frac{4}{6}$ )

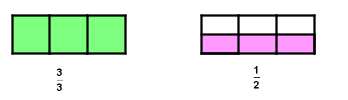
Sandra Hemrich ikonisch Aufgabe3 Einführung.png

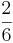(! $\frac{5}{6}$ )( $\frac{3}{6}$ )(! $\frac{4}{6}$ )

→Hier geht`s zur 4. Seite
Hier gehts zurück zur 2.Seite

@@ Zeile 25: / Zeile 25: @@
 <br>
 <br>
+<div style="border: 2px solid blue; background-color:#ffffff; padding:7px;">
 '''Kreuze an! Welche Rechenregel stimmt für <math> \frac{2}{3} </math>&nbsp; von &nbsp; <math> \frac{4}{5} </math>? (siehe Beispiel oben)'''
@@ Zeile 34: / Zeile 35: @@
 (!<math> \frac{2}{3} </math>&nbsp; von &nbsp; <math> \frac{4}{5} </math> = <math> \frac{2 + 4}{3*5} </math>)
 </div>
+&nbsp;
+</div>
 &nbsp;
@@ Zeile 65: / Zeile 68: @@
 &nbsp;&nbsp;&nbsp;&nbsp;2)&nbsp;&nbsp; Ebenfalls werden die '''Nenner''' beider Brüche miteinander '''multipliziert'''   &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;<math> \frac{2}{5} </math> *<math> \frac{3}{4} </math> = <math> \frac{2*3}{5*4} </math>
-&nbsp;&nbsp;&nbsp;&nbsp;3)&nbsp;&nbsp; '''Kürze''' das Ergebnis soweit wie möglich! &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;<math> \frac{10}{12} </math> = <math> \frac{5}{6} </math>
+&nbsp;&nbsp;&nbsp;&nbsp;3)&nbsp;&nbsp; '''Kürze''' das Ergebnis soweit wie möglich! &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;<math> \frac{10}{12} </math> = <math> \frac{5}{6} </math>
-&nbsp;&nbsp;&nbsp;&nbsp;4)&nbsp;&nbsp; Wandle den Bruch (wenn möglich) in eine '''gemischte Zahl'''um.&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;
+)&nbsp;&nbsp;&nbsp;&nbsp;
+Wandle den Bruch(wenn möglich)in eine
+'''gemischte Zahl'''um.&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; nbsp;nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;
 </div>
 &nbsp;

Seite 3: Unterschied zwischen den Versionen

Version vom 18. Oktober 2011, 20:32 Uhr

2.Station: Multiplikation zweier Brüche

Navigationsmenü

Meine Werkzeuge

Namensräume

Varianten

Ansichten

Aktionen

Suche

Navigation

Werkzeuge