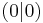Die Quadratische Funktion stellt sich vor: Unterschied zwischen den Versionen
K (Satzbau Satzzeichen Rechtschreibung) |
|||
| (9 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Lernpfad-M|<big>'''Die Quadratische Funktion stellt sich vor'''</big> | {{Lernpfad-M|<big>'''Die Quadratische Funktion stellt sich vor'''</big> | ||
| − | + | __NOCACHE__ | |
| − | + | ||
'''In diesem Lernpfad lernst du die quadratische Funktion kennen! Bearbeite den unten aufgeführten Lernpfad!''' | '''In diesem Lernpfad lernst du die quadratische Funktion kennen! Bearbeite den unten aufgeführten Lernpfad!''' | ||
| Zeile 37: | Zeile 36: | ||
Betrachte die beiden Graphen und löse damit das Quiz! <br> | Betrachte die beiden Graphen und löse damit das Quiz! <br> | ||
Beim Prüfen der Antworten wird dir "rot" angezeigt was du falsch angekreuzt hast. | Beim Prüfen der Antworten wird dir "rot" angezeigt was du falsch angekreuzt hast. | ||
| − | Mit der Farbe "grün" bekommst du die richtigen Ergebnisse | + | Mit der Farbe "grün" bekommst du die richtigen Ergebnisse angezeigt, auch falls du sie nicht angekreuzt hast. Überprüfe im Anschluss deine Ergebnisse und versuche die richtigen Antworten nachzuvollziehen! |
<div class="multiplechoice-quiz"> | <div class="multiplechoice-quiz"> | ||
| Zeile 60: | Zeile 59: | ||
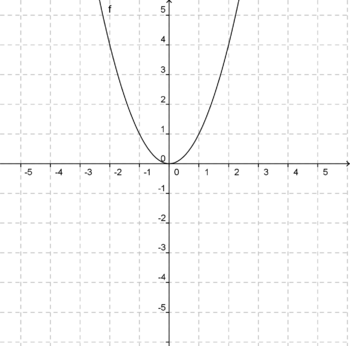
Den Graph der quadratischen Funktion nennt man '''Parabel'''. <br> | Den Graph der quadratischen Funktion nennt man '''Parabel'''. <br> | ||
Es lässt sich feststellen, dass die Parabel symmetrisch zur '''y-Achse''' und nach oben '''geöffnet''' ist. <br> | Es lässt sich feststellen, dass die Parabel symmetrisch zur '''y-Achse''' und nach oben '''geöffnet''' ist. <br> | ||
| − | Die quadratische Funktion besitzt zudem einen tiefsten Punkt im '''Koordinatenursprung''' bei Punkt S | + | Die quadratische Funktion besitzt zudem einen tiefsten Punkt im '''Koordinatenursprung''' bei Punkt S (0|0). <br> |
Dieser Punkt wird als '''Scheitelpunkt S''' oder kurz '''Scheitel''' bezeichnet. | Dieser Punkt wird als '''Scheitelpunkt S''' oder kurz '''Scheitel''' bezeichnet. | ||
</div> | </div> | ||
| Zeile 73: | Zeile 72: | ||
* Der Graph hat einen '''tiefsten''' Punkt | * Der Graph hat einen '''tiefsten''' Punkt | ||
* Der tiefste Punkt heißt '''Scheitelpunkt S''', oder kurz '''Scheitel''' | * Der tiefste Punkt heißt '''Scheitelpunkt S''', oder kurz '''Scheitel''' | ||
| − | * Der Scheitelpunkt liegt im '''Koordinatenursprung''' bei Punkt <math> | + | * Der Scheitelpunkt liegt im '''Koordinatenursprung''' bei Punkt S<math>(0\!\,|\!\,0)</math> |
}} | }} | ||
| Zeile 96: | Zeile 95: | ||
'''Aufgabe:''' | '''Aufgabe:''' | ||
| − | Du siehst hier zwei Koordinatensysteme. In | + | Du siehst hier zwei Koordinatensysteme. In jedem Koordinatensystem sind mehrere Punkte eingezeichnet. Diese Punkte kannst du mit gehaltener linker Maustaste nach oben oder unten verschieben. Des Weiteren gibt es jeweils das Kontrollkästchen "Graph anzeigen", mit dem du nach bearbeiten der Aufgabe dein Ergebnis überprüfen kannst. |
| − | Verschiebe die Punkte so, dass sie genau auf dem | + | Verschiebe die Punkte so, dass sie genau auf dem Graph der jeweiligen Funktion liegen würden und überprüfe dann dein Ergebnis durch Anklicken des Kontrollkästchens. Liegen deine Punkte alle auf dem Graph, so hast du die Aufgabe korrekt gelöst. |
| − | Beginne zunächst mit der linearen Funktion "f(x) = x" und überlege dir dann, wo die Punkte | + | Beginne zunächst mit der linearen Funktion "f(x) = x" und überlege dir dann, wo die Punkte der quadratischen Funktion "f(x) = x²" liegen. |
<br> | <br> | ||
<br> | <br> | ||
| Zeile 118: | Zeile 117: | ||
<big>'''KNIFFELAUFGABE:'''</big> | <big>'''KNIFFELAUFGABE:'''</big> | ||
| − | In dieser Aufgabe soll | + | In dieser Aufgabe soll eine voher gezeigte Eigenschaft genauer betrachtet werden. Löse dafür die kleine Kniffelaufgabe. Keine Angst, sie ist nicht schwer. |
| − | Überprüfe, welche der folgenden Aussagen richtig oder falsch | + | Überprüfe, welche der folgenden Aussagen richtig oder falsch ist und finde das richtige Ergebnis für "x = 3". |
Betrachtet werden soll natürlich die quadratische Funktion "f(x) = x<sup>2</sup>". | Betrachtet werden soll natürlich die quadratische Funktion "f(x) = x<sup>2</sup>". | ||
| Zeile 142: | Zeile 141: | ||
<div class="multiplechoice-quiz"> | <div class="multiplechoice-quiz"> | ||
| − | Was sagt dir dieses Ergebnis? (!Nichts) (Das Ergebnis zeigt die Symmetrieeigenschaft der quadratischen Funktion) (Jedem x-Wert, egal ob positiv oder negativ, wird der | + | Was sagt dir dieses Ergebnis? (!Nichts) (Das Ergebnis zeigt die Symmetrieeigenschaft der quadratischen Funktion) (Jedem x-Wert, egal ob positiv oder negativ, wird der gleiche y-Wert zugeordnet) |
</div> | </div> | ||
<br> | <br> | ||
| Zeile 170: | Zeile 169: | ||
'''f(-x)<math>=</math>f(x), da (-x)<sup>2</sup><math>=</math>(x)<sup>2</sup>''' | '''f(-x)<math>=</math>f(x), da (-x)<sup>2</sup><math>=</math>(x)<sup>2</sup>''' | ||
| − | Begründung: | + | Begründung: Jedem x-Wert, egal ob positiv oder negativ, wird der gleiche y-Wert zugeordnet. |
}} | }} | ||
Aktuelle Version vom 7. November 2018, 09:30 Uhr
|
Lernpfad
|
Auf gehts:
Heute lernen wir eine neue Klasse von Funktionen kennen!
Es handelt sich dabei um die "Quadratische Funktion".
Aus der 8. Jahrgangsstufe kennst du bereits die "Lineare Funktion".
Wir wollen im Folgenden die quadratische Funktion im Vergleich zur linearen Funktion einführen.
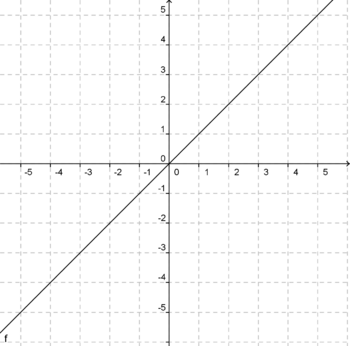
Schau dir jeweils den Graph der linearen und der quadratischen Funktion genau an und bearbeite danach die Aufgaben rechts daneben:
30px Merke
Die quadratische Funktion:
|
Bisher haben wir uns nur den Graph und die Eigenschaften der quadratischen Funktion angeschaut, aber was für eine Funktionsvorschrift verbirgt sich dahinter?
Diesmal bekommst du zuerst das Ergebnis vorgestellst, welches du dir in der anschließenden Aufgabe näher betrachten sollst.
30px Merke
Die quadratische Funktion besitzt die Funktionsgleichung der Form: f(x) Dabei gilt: jeder y-Wert ergibt sich aus dem Quadrat des x-Wertes. |
Aufgabe:
Du siehst hier zwei Koordinatensysteme. In jedem Koordinatensystem sind mehrere Punkte eingezeichnet. Diese Punkte kannst du mit gehaltener linker Maustaste nach oben oder unten verschieben. Des Weiteren gibt es jeweils das Kontrollkästchen "Graph anzeigen", mit dem du nach bearbeiten der Aufgabe dein Ergebnis überprüfen kannst.
Verschiebe die Punkte so, dass sie genau auf dem Graph der jeweiligen Funktion liegen würden und überprüfe dann dein Ergebnis durch Anklicken des Kontrollkästchens. Liegen deine Punkte alle auf dem Graph, so hast du die Aufgabe korrekt gelöst.
Beginne zunächst mit der linearen Funktion "f(x) = x" und überlege dir dann, wo die Punkte der quadratischen Funktion "f(x) = x²" liegen.
| Lineare Funktion | Quadratische Funktion |
|---|---|
|
|
KNIFFELAUFGABE:
In dieser Aufgabe soll eine voher gezeigte Eigenschaft genauer betrachtet werden. Löse dafür die kleine Kniffelaufgabe. Keine Angst, sie ist nicht schwer.
Überprüfe, welche der folgenden Aussagen richtig oder falsch ist und finde das richtige Ergebnis für "x = 3".
Betrachtet werden soll natürlich die quadratische Funktion "f(x) = x2".
| Vorgabe | Richtig/Falsch | Begründung | |
| 1. | -f[x] f[x] f[x] |
falsch |
weil -9 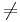 9 9
|
| 2. | f[-x] f[x] f[x] |
richtig |
weil 9  9 9
|
| 3. | -f[x] f[-x] f[-x] |
falsch |
weil -9 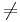 9 9
|
| 4. | -f[-x] f[x] f[x] |
falsch |
weil -9 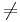 9 9
|
Was sagt dir dieses Ergebnis? (!Nichts) (Das Ergebnis zeigt die Symmetrieeigenschaft der quadratischen Funktion) (Jedem x-Wert, egal ob positiv oder negativ, wird der gleiche y-Wert zugeordnet)
30px Merke
Aufgrund der Symmetrieeigenschaft der quadratischen Funktion gilt: f(-x) Begründung: Jedem x-Wert, egal ob positiv oder negativ, wird der gleiche y-Wert zugeordnet. |
Hier ist die Einführung der quadratischen Funktion "f(x) = x2" abgeschlossen.
In den folgenden Lerneinheiten wird dann mit dieser Funktion gearbeitet. Neue Parameter werden die Parabel verändern, aber siehe selbst!!