Zusammenfassung: Flächeninhalt des Dreiecks: Unterschied zwischen den Versionen
(Unterseite) |
(Abschnitt rechtwinkliges und gleichschenkliges Dreieck eingefügt) |
||
| Zeile 10: | Zeile 10: | ||
|</span> <br> | |</span> <br> | ||
[[Bild:Ebert_MerkbildDreieck.jpg|center]]<br> | [[Bild:Ebert_MerkbildDreieck.jpg|center]]<br> | ||
| + | |} | ||
| + | </div> | ||
| + | |||
| + | '''''Aber Moment, da fehlt doch was, oder? | ||
| + | Bearbeite dazu den nächsten Abschnitt''''' | ||
| + | === Variation am Dreieck=== | ||
| + | : '''''Du siehst hier ein Dreieck, bei dem die Seiten gegeben sind:'''''<br> | ||
| + | *<math>a = 5</math> <br> | ||
| + | *<math>b = 3</math> <br> und | ||
| + | *<math>c =</math> <math>\sqrt{34}</math> | ||
| + | |||
| + | [[Bild:Ebert_rechtwinklig.jpg|center]] | ||
| + | *'''Maja soll den Flächeninhalt des Dreiecks berechnen.'''<br> | ||
| + | <br> | ||
| + | '''"Dazu muss ich erst noch die Länge der Höhe h<sub>c</sub> berechnen. "''' | ||
| + | <br> | ||
| + | *Stimmt das? Muss Maja wirklich erst die Länge der Höhe zur Seite c bestimmen?<br> | ||
| + | |||
| + | *'''Welches spezielle Dreieck ist das Dreieck ABC?''' <br> | ||
| + | Schaffst Du es auch ohne den zweiten Hinweis?<br> | ||
| + | {{ versteckt| Dreieck ABC ist ein rechtwinkliges Dreieck }} | ||
| + | <br> | ||
| + | <br> | ||
| + | *'''Ist nicht schon eine Höhe gegeben, die Maja verwenden kann?''' <br> | ||
| + | Du bist doch schon ein Profi und brauchst sicher nicht den Hinweis, oder? <br> | ||
| + | {{ versteckt| Die Seiten a und b des Dreiecks ABC können jeweils als Grundseite und als dazugehörige Höhe verwendet werden, da das Dreieck ABC rechtwinklig ist und a senkrecht zu b ist.}} | ||
| + | |||
| + | |||
| + | |||
| + | *'''Berechne den Flächeninhalt des Dreiecks''' | ||
| + | |||
| + | <div class="lueckentext-quiz"> | ||
| + | Es gilt zum Beispiel: | ||
| + | Länge Grundseite b: '''3 (cm)'''<br> | ||
| + | Länge der zugehörigen Höhe a : 5 cm <br> | ||
| + | Der Flächeninhalt des Dreiecks beträgt '''7,5 (cm²)''' | ||
| + | </div> | ||
| + | |||
| + | <div style="border: 2px solid red; background-color:#ffffff; padding:7px;"> | ||
| + | {| | ||
| + | |[[Bild:Ebert_MotivatorMerke.jpg|200px]]|| '''Der Flächeninhalt eines rechtwinkligen Dreiecks berechnet sich durch''' : | ||
| + | :::::::::F<sub>rechtwinklig</sub> = '''<math>{1 \over 2}</math>''' <math>\cdot</math> <span style="color: green">'''b'''</span> <math>\cdot</math> <span style="color: blue">'''a'''</span> | ||
| + | |||
| + | '''wobei <span style="color: blue">'''a'''</span> und <span style="color: green">'''b'''</span> senkrecht zu einander stehen.''' | ||
| + | <br> | ||
| + | |} | ||
| + | </div> | ||
| + | |||
| + | ====Wie lautet die Flächeninhaltsformel für ein...====<br> | ||
| + | :'''..gleichschenklig-rechtwinkliges Dreieck ABC aus?''' | ||
| + | :'''Der rechte Winkel befindet sich am Eckpunkt C.''''' | ||
| + | [[Bild:Ebert_gleichschenklig.jpg|center]] | ||
| + | <div style="border: 2px solid red; background-color:#ffffff; padding:7px;"> | ||
| + | {| | ||
| + | :'''''Ergänze die fehlenden Felder und ermittle daraus die Flächeninhaltsformel für das gleichschenklig-rechtwinklige Dreieck:''''' | ||
| + | <div class="lueckentext-quiz"> | ||
| + | 1. Im gleichschenkligen Dreieck gilt für die Seiten f und e:<br> | ||
| + | ::::f = e | ||
| + | 2. Flächeninhaltsformel des rechtwinkligen Dreiecks:<br> | ||
| + | :::F<sub>rechtwinklig</sub> = '''<math>{1 \over 2}</math>''' <math>\cdot</math> '''e''' <math>\cdot</math> f <br> | ||
| + | <math>\Rightarrow</math> Für den Flächeninhalt F eines rechtwinkligen und gleichschenkligen Dreiecks gilt: | ||
| + | F = '''<math>{1 \over 2}</math>''' <math>\cdot</math> '''e''' <math>\cdot</math> e = '''e²''' | ||
| + | </div> | ||
|} | |} | ||
</div> | </div> | ||
[[Übungsaufgaben zur Flächenberechnung am Dreieck]] | [[Übungsaufgaben zur Flächenberechnung am Dreieck]] | ||
Version vom 15. Juli 2009, 17:27 Uhr
Übertrage den roten Merkkasten in dein Heft, damit Du die Flächeninhaltsformel für Dreiecke auch Zuhause nachschauen kannst:
 |
Den Flächeninhalt des Dreiecks berechnet man durch
mit g als Grundseite und h als der dazugehörigen Höhe. |
|
Aber Moment, da fehlt doch was, oder? Bearbeite dazu den nächsten Abschnitt
Variation am Dreieck
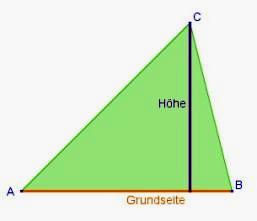
- Du siehst hier ein Dreieck, bei dem die Seiten gegeben sind:
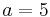
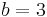
und
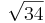
- Maja soll den Flächeninhalt des Dreiecks berechnen.
"Dazu muss ich erst noch die Länge der Höhe hc berechnen. "
- Stimmt das? Muss Maja wirklich erst die Länge der Höhe zur Seite c bestimmen?
- Welches spezielle Dreieck ist das Dreieck ABC?
Schaffst Du es auch ohne den zweiten Hinweis?
- Ist nicht schon eine Höhe gegeben, die Maja verwenden kann?
Du bist doch schon ein Profi und brauchst sicher nicht den Hinweis, oder?
- Berechne den Flächeninhalt des Dreiecks
Es gilt zum Beispiel:
Länge Grundseite b: 3 (cm)
Länge der zugehörigen Höhe a : 5 cm
Der Flächeninhalt des Dreiecks beträgt 7,5 (cm²)
 |
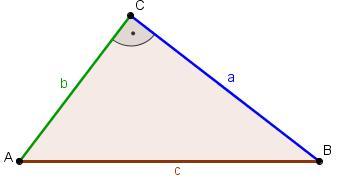
Der Flächeninhalt eines rechtwinkligen Dreiecks berechnet sich durch :
wobei a und b senkrecht zu einander stehen.
|
====Wie lautet die Flächeninhaltsformel für ein...====
- ..gleichschenklig-rechtwinkliges Dreieck ABC aus?
- Der rechte Winkel befindet sich am Eckpunkt C.
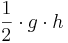


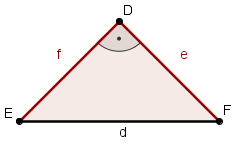
 Für den Flächeninhalt F eines rechtwinkligen und gleichschenkligen Dreiecks gilt:
F =
Für den Flächeninhalt F eines rechtwinkligen und gleichschenkligen Dreiecks gilt:
F = 
