3.Station: Unterschied zwischen den Versionen
K |
K |
||
| (8 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
<div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;"> | <div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;"> | ||
| − | [[ | + | [[Lernpfade/Zentrische Streckung/Abbildung durch zentrische Streckung|1. Station: Ähnlichkeitsabbildung]] - [[Lernpfade/Zentrische Streckung/Abbildung durch zentrische Streckung/Hier kannst du weitere Beispiele einer zentrischen Streckung sehen|Exkurs: Weitere Beispiele einer zentrischen Streckung]] - [[Lernpfade/Zentrische Streckung/Abbildung durch zentrische Streckung/2.Station|2. Station: Streckungsfaktor]] - [[Lernpfade/Zentrische Streckung/Abbildung durch zentrische Streckung/2.Station Fortsetzung|Fortsetzung der 2. Station: Streckungsfaktor]] - [[Lernpfade/Zentrische Streckung/Abbildung durch zentrische Streckung/3.Station|3. Station: Berechnung der Streckenlängen und des Streckungsfaktors]] - [[Lernpfade/Zentrische Streckung/Abbildung durch zentrische Streckung/4.Station|4. Station: Zusammenfassung]] - [[Lernpfade/Zentrische Streckung/Abbildung durch zentrische Streckung/5.Station|5. Station: Übung]] - [[Lernpfade/Zentrische Streckung/Abbildung durch zentrische Streckung/6.Station|6. Station: Wissenswertes]] |
</div> | </div> | ||
<br> | <br> | ||
==3. Station: Berechnung der Streckenlängen und des Streckungsfaktors== | ==3. Station: Berechnung der Streckenlängen und des Streckungsfaktors== | ||
| − | + | Wie du in der 2. Station schon herausgefunden hast, ist die Bildstrecke |k|-mal so lang wie die Urbildstrecke.<br> | |
| − | + | Geometrisch bedeutet dies für einen beliebigen Punkt P: <math> \overline{ZP'} = \mid k\mid \cdot \overline{ZP}</math><br> | |
| − | + | Daraus folgt: <math>\mid k\mid = {\overline{ZP'}\over\overline{ZP}}</math><br> | |
<br> | <br> | ||
| − | + | Ob dies auch zur Berechnung von Strecken, die nicht durch den Punkt Z verlaufen, gilt, kannst du durch Umformung herausfinden. <br> | |
| − | + | Ziehe dafür den richtigen Ausdruck in die passende Lücke:<br> | |
| − | <div style="border: 2px solid # | + | <div style="border: 2px solid #0000ff; background-color:#ffffff; padding:7px;"> |
{| | {| | ||
|[[Bild:Porzelt_Streckenlänge.jpg]]|| | |[[Bild:Porzelt_Streckenlänge.jpg]]|| | ||
| Zeile 24: | Zeile 24: | ||
</div> | </div> | ||
<br> | <br> | ||
| − | + | [[Bild:Porzelt_lobenderPanto3.jpg]] | |
<br> | <br> | ||
| − | <div align="left">[[ | + | <div align="left">[[Lernpfade/Zentrische Streckung/Abbildung durch zentrische Streckung/4.Station|<math>\Rightarrow</math> Weiter zur 4. Station: Zusammenfassung]]</div> |
| + | <br> | ||
| + | <div align="left">[[Lernpfade/Zentrische Streckung/Abbildung durch zentrische Streckung/2.Station Fortsetzung|<math>\Leftarrow</math> Zurück zur Fortsetzung der 2. Station: Streckungsfaktor]]</div> | ||
Aktuelle Version vom 6. August 2009, 14:27 Uhr
1. Station: Ähnlichkeitsabbildung - Exkurs: Weitere Beispiele einer zentrischen Streckung - 2. Station: Streckungsfaktor - Fortsetzung der 2. Station: Streckungsfaktor - 3. Station: Berechnung der Streckenlängen und des Streckungsfaktors - 4. Station: Zusammenfassung - 5. Station: Übung - 6. Station: Wissenswertes
3. Station: Berechnung der Streckenlängen und des Streckungsfaktors
Wie du in der 2. Station schon herausgefunden hast, ist die Bildstrecke |k|-mal so lang wie die Urbildstrecke.
Geometrisch bedeutet dies für einen beliebigen Punkt P: 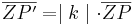
Daraus folgt: 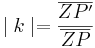
Ob dies auch zur Berechnung von Strecken, die nicht durch den Punkt Z verlaufen, gilt, kannst du durch Umformung herausfinden.
Ziehe dafür den richtigen Ausdruck in die passende Lücke:
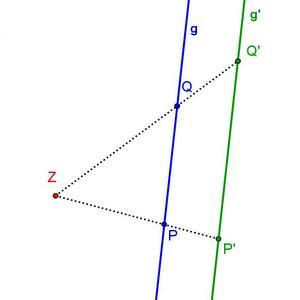 |
ZP' = |k| ∙ ZP und ZQ' = |k| ∙ ZQ |


 Zurück zur Fortsetzung der 2. Station: Streckungsfaktor
Zurück zur Fortsetzung der 2. Station: Streckungsfaktor
