Vertiefen und Erweitern zum Flächeninhalt des Dreiecks: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
K (→‎Herleitungsidee 3)
K (→‎Herleitungsidee 3: Rechtschreibfehler verbessert)
 
(3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 46: Zeile 46:
 
<div class="lueckentext-quiz">
 
<div class="lueckentext-quiz">
 
*Sie schreiben ihre Lösungswege auf. Welcher Lösungsweg passt zu den Skizzen?
 
*Sie schreiben ihre Lösungswege auf. Welcher Lösungsweg passt zu den Skizzen?
−
*Nils rechnet so: F<sub>Dreieck</sub> = ( 8 <math>\cdot</math> 3 ): 2= 12 . Das gehört zur '''Skizze I'''
+
*Nils rechnet so: F<sub>Dreieck</sub> = ( 8 cm<math>\cdot</math> 3 cm): 2= 12cm² . Das gehört zur '''Skizze I'''
−
*Maja rechnet so: F<sub>Dreieck</sub> = 8 <math>\cdot</math> ( 3 : 2 ) = 8 <math>\cdot</math> 1,5 = 12 : Das gehört zur '''Skizze II'''
+
*Maja rechnet so: F<sub>Dreieck</sub> = 8 cm<math>\cdot</math> ( 3cm : 2 ) = 8cm <math>\cdot</math> 1,5cm = 12cm² : Das gehört zur '''Skizze II'''
 
</div>
 
</div>
 
<br>
 
<br>
Zeile 61: Zeile 61:
 
<br>
 
<br>
 
<br>
 
<br>
−
 
  
 
==<span style="color: green">Suche Dir aus den nächsten beiden Herleitungen ''eine'' aus und bearbeite diese</span>==
 
==<span style="color: green">Suche Dir aus den nächsten beiden Herleitungen ''eine'' aus und bearbeite diese</span>==
Zeile 112: Zeile 111:
 
Der Flächeninhalt des Dreiecks ABC ist: '''8 (Zahl eintragen)'''cm²
 
Der Flächeninhalt des Dreiecks ABC ist: '''8 (Zahl eintragen)'''cm²
 
</div>
 
</div>
−
'''''Berechne den Flächeninhalt des <span style="color:green">Dreiecks M<sub>a</sub>M<sub>b</sub>C</span>. Überlege, welche Länge die <span style="color: red">Strecke [ M<sub>a</sub>M<sub>b</sub>]</span> besitzt.'''''<br>
+
'''''Berechne den Flächeninhalt des <span style="color:green">Dreiecks M<sub>b</sub>M<sub>a</sub>C</span>. Überlege, welche Länge die <span style="color: red">Strecke [ M<sub>a</sub>M<sub>b</sub>]</span> besitzt.'''''<br>
 
<div class="lueckentext-quiz">
 
<div class="lueckentext-quiz">
−
Der Flächeninhalt des Dreiecks M<sub>a</sub>M<sub>b</sub>C ist '''2(Zahl eintragen)''' cm².
+
Der Flächeninhalt des Dreiecks M<sub>b</sub>M<sub>a</sub>C ist '''2(Zahl eintragen)''' cm².
 
</div>
 
</div>
 
'''''Berechne den Flächeninhalt des Parallelogramms.'''''  
 
'''''Berechne den Flächeninhalt des Parallelogramms.'''''  
Zeile 141: Zeile 140:
 
'''''Wie Du siehst, ähneln sich diese beiden Herleitungsideen 2 und 3:'''''<br>
 
'''''Wie Du siehst, ähneln sich diese beiden Herleitungsideen 2 und 3:'''''<br>
 
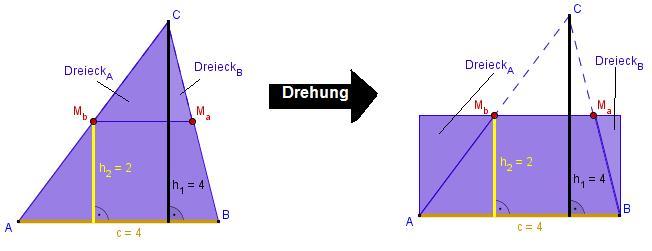
*'''In der ersten Variante zerlegt man das Dreieck geeignet und ergänzt zum <span style="color: red">Rechteck</span>  mit gleicher Grundseite und halber Höhe...<br> '''
 
*'''In der ersten Variante zerlegt man das Dreieck geeignet und ergänzt zum <span style="color: red">Rechteck</span>  mit gleicher Grundseite und halber Höhe...<br> '''
−
[[Bild:Ebert_Herleitung2.jpg|300px|center]]
+
[[Bild:Ebert_Herleitung2.jpg|center]]
 
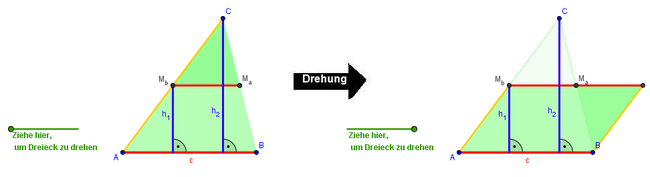
*'''und in der zweiten Variante zerlegt man das Dreieck und ergänzt zu einem <span style="color: red">Parallelogramm</span> mit gleicher Länge der Grundseite und halber Höhe'''   
 
*'''und in der zweiten Variante zerlegt man das Dreieck und ergänzt zu einem <span style="color: red">Parallelogramm</span> mit gleicher Länge der Grundseite und halber Höhe'''   
−
[[Bild:Ebert_Herleitung3.jpg|300px|center]]
+
[[Bild:Ebert_Herleitung3.jpg|650px|center]]
 
<br>
 
<br>
 
<br>
 
<br>

Aktuelle Version vom 18. August 2009, 18:33 Uhr

Für die ganz Schnellen:

Vertiefen und Erweitern


Du hast nun eine Möglichkeit kennen gelernt, wie man die Flächeninhaltsformel für Dreiecke herleiten kann. '
Dies ist aber natürlich nicht der einzige Weg.
Versuche die nächsten nachzuvollziehen.
Ebert Motivatoren.jpg






Herleitungsidee 2
  1. Welche Figur entsteht?
  2. Um welche Punkte werden die Teildreiecke gedreht? Um wieviel Grad werden sie gedreht?
  3. Welche Höhe besitzt die neue Figur, im Vergleich zum Ursprungsdreieck?
  4. Welche Länge hat die Grundseite c im Vergleich zur Ausgangsfigur?
  5. Berechne den Flächeninhalt des Dreiecks. Hinweis [Anzeigen]

Das Dreieck hat einen Flächeninhalt von (Zahl eintragen)cm²


Vergleiche Deine Lösungen mit der von Maja: [Lösung anzeigen]


Ebert Motivatoren.jpg
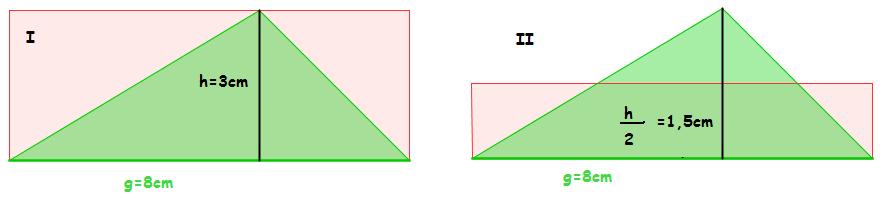
  • Maja und Nils berechnen den Flächeninhalt des grünen Dreiecks.
Ebert Rechenbeispiel.jpg
  • Sie schreiben ihre Lösungswege auf. Welcher Lösungsweg passt zu den Skizzen?
  • Nils rechnet so: FDreieck = ( 8 cm\cdot 3 cm): 2= 12cm² . Das gehört zur                    
  • Maja rechnet so: FDreieck = 8 cm\cdot ( 3cm : 2 ) = 8cm \cdot 1,5cm = 12cm² : Das gehört zur                    

Skizze IISkizze I













Suche Dir aus den nächsten beiden Herleitungen eine aus und bearbeite diese

Herleitungsidee 3

Aufgabenstellung: Kreuze die richtigen Antworten an:

1. Welche Figur ensteht? Es ensteht ein...

Parallelogramm
Rechteck
Trapez
Dreieck

2. Um welchen Punkt wird das Teildreieck gedreht?

Mittelpunkt Ma der Seite a
Mittelpunkt Mb der Seite b
Eckpunkt C

3. Um wieviel Grad wird es gedreht?

90°
180°
120°
360°

4. Welche Höhe besitzt die neue Figur im Vergleich zum Dreieck ABC? Sie ist...

genauso groß, wie die des Dreiecks ABC
halb so groß, wie die des Dreiecks ABC
doppelt so groß, wie die des Dreiecks ABC

Punkte: 0 / 0


5. Wie entsteht diese Figur?
Du kannst das bestimmt ohne Hinweis lösen, oder? [Anzeigen]

6. Berechne den Flächeninhalt des Dreiecks ABC, wenn h2= 4cm und c= 4cm ist

Der Flächeninhalt des Dreiecks ABC ist: (Zahl eintragen)cm²

Berechne den Flächeninhalt des Dreiecks MbMaC. Überlege, welche Länge die Strecke [ MaMb] besitzt.

Der Flächeninhalt des Dreiecks MbMaC ist (Zahl eintragen) cm².

Berechne den Flächeninhalt des Parallelogramms.

Der Flächeninhalt des Parallelogramms ist: (Zahl eintragen) cm².



Wie kann man für diese Methode die Flächeninhaltsformel des Dreiecks herleiten??

  • Es gilt:

FParallelogramm =                    

  • Aufgrund der Zerlegungsgleichheit gilt:

FParallelogramm =                    

  • Für die Höhen gilt:
                    =                     \cdot h2
  • Einsetzen in Formel für Parallelogramm:
FDreieck =                    

{1 \over 2} g \cdot h2h1FDreieckg \cdot h1{1 \over 2}


Ebert MotivatorRot.jpg Wie Du siehst, ähneln sich diese beiden Herleitungsideen 2 und 3:

  • In der ersten Variante zerlegt man das Dreieck geeignet und ergänzt zum Rechteck mit gleicher Grundseite und halber Höhe...
Ebert Herleitung2.jpg
  • und in der zweiten Variante zerlegt man das Dreieck und ergänzt zu einem Parallelogramm mit gleicher Länge der Grundseite und halber Höhe
Ebert Herleitung3.jpg











Herleitungsidee 4
  1. Welche Figur ensteht?
  2. Um welche Punkte werden jeweils die Teildreiecke gedreht? Um wieviel Grad werden sie gedreht?
  3. Welche Höhe besitzt die erhaltene Figur?
  • Vergleiche Deine Lösungen mit Maja´s Lösungen.
    Ebert MotivatorGrün.jpg

[Lösung anzeigen]


4. Zeige, dass die Grundseite g der neuen Figur halb so lang ist, wie die Grundseite des Dreiecks!
Tipp: Ergänze zum Rechteck und beobachte dabei die Teilstrecken s und t

  • Die Grundseite des Dreiecks setzt sich zusammen aus:

                    = s + s + t + t
Vereinfachen liefert: gDreieck =                     + 2\cdot                     = 2 \cdot(s + t)

  • Für die Grundseite des Rechtecks gilt:

gRechteck=                    

  • Setzt man gRechteck in die Formel für gDreieck und stellt um, so erhält man:

=> gRechteck =                    

s + tt2 \cdot s{1 \over 2} \cdot gDreieckgDreieck


Wie kann man daraus die Flächeninhaltsformel für das Dreieck berechnen?
  • Für den Flächeninhalt des Rechtecks gilt:

FRechteck =                     \cdot h

  • Aufgrund der Zerlegungsgleichheit gilt:
FRechteck =                    
  • Für die Grundseiten gilt:
gRechteck = {1 \over 2} \cdot                    
  • Einsetzen in Flächeninhaltsformel für das Rechteck:
FDreieck =                    

FDreieckgRechteckgDreieck{1 \over 2} gDreieck \cdot h



Ebert Maja.jpg
Ebert Lob3.jpg

Wow! Maja und Nils sind stolz auch Dich. Du hast nun auch den 3. Lernpfad erfolgreich bearbeitet!!'








Hier geht es zurück zur Seite:

Übungsaufgaben zur Flächenberechnung am Dreieck

Von „http://dmuw.zum.de/index.php?title=Vertiefen_und_Erweitern_zum_Flächeninhalt_des_Dreiecks&oldid=4481“