Quader: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
(→‎Übungen)
(→‎Übungen)
Zeile 181: Zeile 181:
 
{  
 
{  
 
| type="{}" }
 
| type="{}" }
−
[[Bild:Quader-Bausteine3.png|150px]] Anzahl der Bausteine: { 19 }
+
[[Bild:Quader-Bausteine3.png|100px]] Anzahl der Bausteine: { 19 }
  
 
{  
 
{  

Version vom 31. August 2009, 14:24 Uhr


Mathematik-digital Pfeil-3d.png
Lernpfad

Quader

In diesem Lernpfad erfährst du viel über einen geometrische Körper, der dir jeden Tag begegnet: der Quader.
Die Bausteine:

  • Beispiele für Quader im Alltag
  • Kantenlängen des Quaders
  • Senkrechte und parallele Kanten
  • Definition für Quader und Zeichnung eines Schrägbilds
  • Übungen

Für die Bearbeitung des Lernpfads benötigst du das Arbeitsblatt, Bleistift, Buntstifte und ein Lineal.

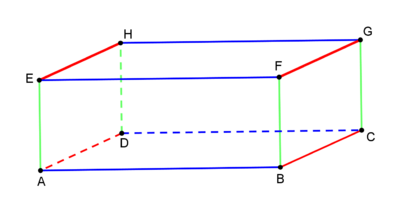
Finde heraus welche Kanten die selbe Länge haben

Welche der folgenden Aussagen ist richtig?

Dieser Quader soll dir eine Hilfe sein:

Klicke auf ein Kästchen, um dir die entsprechende Kante in der Zeichnung anzeigen zu lassen.

Wähle die richtigen Antworten aus und klicke anschließend zur Korrektur auf prüfen.

( \overline {AB} = \overline {HG} ) (! \overline {AB} = \overline {EH} )

( \overline {EH} = \overline {FG} ) (! \overline {EH} = \overline {CG} )

(! \overline {CG} = \overline {EH} ) ( \overline {AE} = \overline {CG} )


Gut gemacht! Das solltest du gleich auf deinem Arbeitsblatt festhalten:
Markiere in der Zeichnung die Kanten mit jeweils der selben Länge in der selben Farbe, wie auch in dieser Zeichnung. Unterstreiche auch den richtigen Begriff in der selben Farbe. Benutze dafür Buntstifte und ein Lineal.

Emmerling-Quader4.png


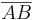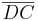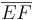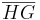l = \overline {AB} = \overline {DC} = \overline {EF} = \overline {HG} ist die Länge des Quaders,


b = 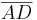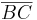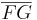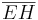\overline {AD} = \overline {BC} = \overline {FG} = \overline {EH} nennt man die Breite des Quaders


und mit h = 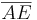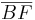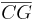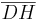\overline {AE} = \overline {BF} = \overline {CG} = \overline {DH} wird die Höhe des Quaders bezeichnet.






Senkrechte und parallele Kanten

Der Quader ist ein Körper, der aus rechteckigen Flächen besteht.
Das Rechteck kennst du bereits. Erinnerst du dich an die Eigenschaften des Rechtecks?
Genau, benachbarte Kanten stehen senkrecht aufeinander und gegenüber liegende Kanten sind parallel!

Welche Kanten des Quaders stehen senkrecht aufeinander?
Wichtig: In einem Quader stehen alle Kanten, die einen Punkt gemeinsam haben aufeinander senkrecht!
 Betrachte diese Zeichnung und überlege dir: Welche Kanten des Quaders stehen senkrecht auf [EF]? Wenn du Hilfe brauchst, dann klicke auf die Kästchen unter dem Bild.


Die Kanten [AE], [EH], [BF] und [FG] stehen senkrecht auf [EF].


Welche Kanten des Quaders sind parallel zueinander?
Wichtig: In einem Quader sind genau die Kanten parallel, die keinen Punkt gemeinsam haben!
 Überlege dir nun anhand der Zeichnung, welche Kanten des Quaders parallel zu [EF] sind.


Die Kanten [AB], [DC] und [HG] sind parallel zu [EF].


Du weißt jetzt schon wann Quaderkanten senkrecht aufeinander stehen oder zueinander parallel sind.

Teste dein Wissen mit diesem Quiz!


Entscheide, welche der Kanten senkrecht auf [BF] stehen, welche parallel zu [BF] sind. Ziehe die Kanten in das richtige Feld und klicke danach auf prüfen.
Kanten, die senkrecht auf [BF] stehen [AB ] [BC] [EF] [FG]
Kanten, die parallel zu [BF] sind [AE] [CG] [EH]

Brauchst du Hilfe?

Zur Erinnerung:

Quaderkanten, die senkrecht aufeinander stehen, haben einen Punkt gemeinsam.

Parallele Quaderkanten haben keinen gemeinsamen Punkt.




Finde eine Definition für Quader selbst heraus

Welcher Begriff passt in die Lücke?


Betrachte genau das Bild!
Es soll dir bei der Bearbeitung der Aufgabe helfen.

Bild-Emmerling.Quader1

Ein Quader ist ein geometrischer Körper, der von sechs ____________ begrenzt wird. (!Strecken) (Flächen) (!Winkeln)

Alle Begrenzungsflächen sind _____________. (Rechtecke) (!Dreiecke) (!Quader)

Jeder Quader besitzt zwölf _____________. (!Flächen) (!Ecken) (Kanten)

Außerdem hat jeder Quader acht ____________. (!Flächen) (Ecken) (!Kanten)

In jeder Ecke treffen sich drei Kanten. Diese benachbarten Kanten stehen aufeinander ____________. (senkrecht) (!parallel) (!schief)



Super! Du kennst dich schon gut mit Quadern aus! Übernimm nun die Definition auf dein Arbeitsblatt, zusammen mit einer Zeichnung eines Quaders.

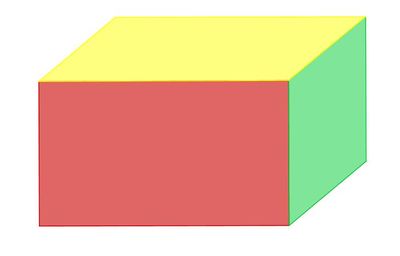
Man zeichnet ein Schrägbild, um einen Quader in der Zeichenebene darzustellen.

Sieh dir das Video genau an und erstelle selbst eine Zeichnung eines Quaders auf dein Arbeitsblatt.
Benutze dafür Lineal und Bleistift und orientiere dich an dem Kästchenmuster auf deinem Arbeitsblatt.
Länge: 5 LE, Breite: 2 LE, Höhe: 3 LE

Du kannst das Video auch anhalten, falls du manche Bilder genauer betrachten möchtest, und du kannst es auch mehrmals ansehen.




Übungen

Nur Übung macht den Meister!

1. Übung

Emmerling-Quader-Milch1.jpg

Hans liebt Cornflakes mit Milch über alles. Am liebsten würde er Cornflakes zum Frühstück, Mittagessen und Abendessen verdrücken.
Wenn er einkaufen geht, dann nimmt er sich gleich immer so viel Milch mit, dass sie für die ganze Woche reicht.
Emmerling-Kiste-Milch2.png
Wie viele der blauen Milchtüten passen in die rote Kiste?
Rechne schriftlich auf deinem Arbeitsblatt!


Hier kannst du deine Rechnung überprüfen:

Schiebe die blauen Milchtüten in die Kiste. Wie viele passen hinein?




2. Übung

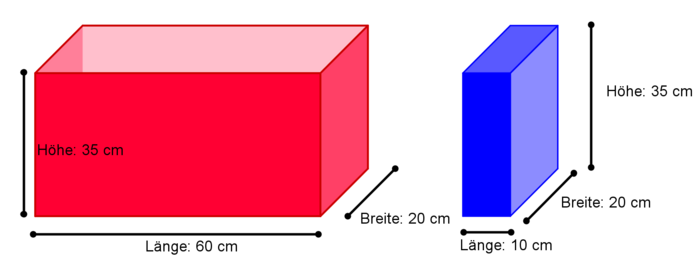
Aus wievielen kleinen Quadern bestehen die großen Quader?
Sieh genau hin und zähle!

1.

Quader-Bausteine3.png Anzahl der Bausteine:

2.

Quader-Bausteine2.png Anzahl der Bausteine:

3.

Quader-Bausteine1.png Anzahl der Bausteine:

Punkte: 0 / 0




3. Übung

Hier siehst du das Schrägbild eines Quaders.


Schätze ab!

Welche Begrenzungsflächen des Quaders sind am größten? (!Deckfäche) (!Rückfläche) (!Seitenfläche ADHE) (!Seitenfläche BCGF) (!Vorderfläche) (!Grundfläche)

Welche Begrenzungsflächen des Quaders sind am größten? (!Deckfäche) (!Rückfläche) (!Seitenfläche ADHE) (!Seitenfläche BCGF) (!Vorderfläche) (!Grundfläche)


Rechne schriftlich auf deinem Arbeitsblatt und prüfe anschließend dein Ergebnis hier:

1.

Umfang der Vorderfläche: cm

2.

Umfang der Deckfläche: cm

3.

Umfang einer Seitenfläche: cm

Punkte: 0 / 0



Du warst schnell und bist schon fertig? Super! Dann bearbeite diese kniffelige Extraaufgabe:

Betrachte noch einmal genau das Schrägbild des Quaders in der 3. Übung!
Welche Gesamtlänge berechnet sich aus allen Seitenlängen?
Rechne möglichst geschickt auf deinem Arbeitsblatt!

(!1 cm) (!2 cm) (!3 cm)



Dein Tag ist voll mit Quadern! Sieh dich heute mal genau um. Zu Hause, unterwegs und in der Schule, überall kannst du Quader entdecken!
Notiere die Quader, die dir heute besonders auffallen auf dein Arbeitsblatt!


\Leftarrow Zurück zur Übersicht
\Rightarrow Zum Lernpfad "Würfel"
Von „http://dmuw.zum.de/index.php?title=Lernpfade/Quader_und_Quadernetze/Quader&oldid=4958“