Prinzipielle Grenzen der Berechenbarkeit: Unterschied zwischen den Versionen
(→Aufgabe) |
|||
| Zeile 8: | Zeile 8: | ||
|} | |} | ||
</div> | </div> | ||
| − | + | {{Aufgabe-Mathe| | |
| − | + | ||
Die 26 Buchstaben des Alphabets werden mit den Zahlen 1 bis 26 kodiert. Damit könnte man ein geschriebenes Wort als Zahl schreiben. Dekodiere die Zahl "26235945212097"! | Die 26 Buchstaben des Alphabets werden mit den Zahlen 1 bis 26 kodiert. Damit könnte man ein geschriebenes Wort als Zahl schreiben. Dekodiere die Zahl "26235945212097"! | ||
| − | + | Welche Buchstabenfolge erhält man nach dem Dekodieren? | |
| − | + | ZWEIDEUTIG oder was anderes | |
| + | }} | ||
| + | |||
| + | {{Aufgabe-Mathe| | ||
Nun werden die 26 Buchstaben des Alphabets wie folgt kodiert: | Nun werden die 26 Buchstaben des Alphabets wie folgt kodiert: | ||
Den 26 Buchstaben des Alphabets wird jeweils eine eindeutige Zahl zwischen 1 und 26 zugeordnet. Ein Wort wird nun mit fortlaufenden Primzahlpotenzen kodiert, also wenn a die Zahl 1, b die Zahl 2, c die Zahl 3 zugeordnet wird, dann wird das Wort abbca wie folgt kodiert: | Den 26 Buchstaben des Alphabets wird jeweils eine eindeutige Zahl zwischen 1 und 26 zugeordnet. Ein Wort wird nun mit fortlaufenden Primzahlpotenzen kodiert, also wenn a die Zahl 1, b die Zahl 2, c die Zahl 3 zugeordnet wird, dann wird das Wort abbca wie folgt kodiert: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | * a ist der erste Buchstabe des Wortes und 2 die erste Primzahl. Also wird das a mit <math>2^1=2</math> kodiert. | |
| + | * b ist der zweite Buchstabe des Wortes und 3 die zweite Primzahl. Also wird das b mit <math>3^2=9</math> kodiert. | ||
| + | * b ist der dritte Buchstabe des Wortes und 5 die dritte Primzahl. Also wird dieses b mit <math>5^2=25</math> kodiert. | ||
| + | * c ist der vierte Buchstabe des Wortes und 7 die vierte Primzahl. Also wird das c mit <math>7^3=343</math> kodiert. | ||
| + | * a ist der fünfte Buchstabe des Wortes und 11 die fünfte Primzahl. Also wird dieses a mit <math>11^1=11</math> kodiert. | ||
| + | Multipliziert man diese Zahlen miteinander, erhält man die Zahl <math>2*9*25*343*11=1697850</math>. | ||
Da die Primfaktorzerlegung eindeutig ist, wenn man die Primzahlpotenzen nach der größe der Primzahlen ordnet, kann man aus jeder Zahl das zugehörige Wort erzeugen. | Da die Primfaktorzerlegung eindeutig ist, wenn man die Primzahlpotenzen nach der größe der Primzahlen ordnet, kann man aus jeder Zahl das zugehörige Wort erzeugen. | ||
| + | Welche Buchstabenfolge erhält man, wenn man die Zahl *** dekodiert? | ||
| + | }} | ||
| − | + | {{Aufgabe-Mathe| | |
| − | + | ||
| − | + | ||
Nun werden die 26 Buchstaben des Alphabets mit den Zahlen 01 bis 26 kodiert. Schreibt man die kodierten Buchstaben hintereinander, so erhält man eine Zahl. Dekodiere die Zahl 26230509060512121519. | Nun werden die 26 Buchstaben des Alphabets mit den Zahlen 01 bis 26 kodiert. Schreibt man die kodierten Buchstaben hintereinander, so erhält man eine Zahl. Dekodiere die Zahl 26230509060512121519. | ||
| + | }} | ||
| + | ZWEIFELLOS | ||
<div class="multiplechoice-quiz"> | <div class="multiplechoice-quiz"> | ||
Welches Verfahren eignet sich für eine Gödelisierung? (!Kodierung mit Zahlen 1 bis 26) (Kodierung mit Zahlen 01 bis 26) (Kodierung mit Primzahlpotenzen)(!Keines der Verfahren) | Welches Verfahren eignet sich für eine Gödelisierung? (!Kodierung mit Zahlen 1 bis 26) (Kodierung mit Zahlen 01 bis 26) (Kodierung mit Primzahlpotenzen)(!Keines der Verfahren) | ||
</div> | </div> | ||
Version vom 13. September 2009, 17:15 Uhr
Ich packe meinen Koffer...
Fülle den Reisekoffer optimal aus und lege nichtbenötigte Gegenstände in die Ablage!
| Koffer | Taschenlampe (15€) | 60px | Ameise | Motte | |
| Ablage | Pflaume | 60px | Apfel | Kirsche | Banane |
|
Die 26 Buchstaben des Alphabets werden mit den Zahlen 1 bis 26 kodiert. Damit könnte man ein geschriebenes Wort als Zahl schreiben. Dekodiere die Zahl "26235945212097"! Welche Buchstabenfolge erhält man nach dem Dekodieren? ZWEIDEUTIG oder was anderes |
|
Nun werden die 26 Buchstaben des Alphabets wie folgt kodiert: Den 26 Buchstaben des Alphabets wird jeweils eine eindeutige Zahl zwischen 1 und 26 zugeordnet. Ein Wort wird nun mit fortlaufenden Primzahlpotenzen kodiert, also wenn a die Zahl 1, b die Zahl 2, c die Zahl 3 zugeordnet wird, dann wird das Wort abbca wie folgt kodiert:
Multipliziert man diese Zahlen miteinander, erhält man die Zahl |
|
Nun werden die 26 Buchstaben des Alphabets mit den Zahlen 01 bis 26 kodiert. Schreibt man die kodierten Buchstaben hintereinander, so erhält man eine Zahl. Dekodiere die Zahl 26230509060512121519. |
ZWEIFELLOS
Welches Verfahren eignet sich für eine Gödelisierung? (!Kodierung mit Zahlen 1 bis 26) (Kodierung mit Zahlen 01 bis 26) (Kodierung mit Primzahlpotenzen)(!Keines der Verfahren)
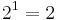 kodiert.
kodiert.
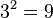 kodiert.
kodiert.
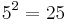 kodiert.
kodiert.
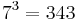 kodiert.
kodiert.
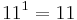 kodiert.
kodiert.
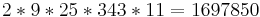 .
Da die Primfaktorzerlegung eindeutig ist, wenn man die Primzahlpotenzen nach der größe der Primzahlen ordnet, kann man aus jeder Zahl das zugehörige Wort erzeugen.
Welche Buchstabenfolge erhält man, wenn man die Zahl *** dekodiert?
.
Da die Primfaktorzerlegung eindeutig ist, wenn man die Primzahlpotenzen nach der größe der Primzahlen ordnet, kann man aus jeder Zahl das zugehörige Wort erzeugen.
Welche Buchstabenfolge erhält man, wenn man die Zahl *** dekodiert?

