Lösungsvorschlag iii): Unterschied zwischen den Versionen

Version vom 28. September 2009, 01:03 Uhr

Lösungsweg:

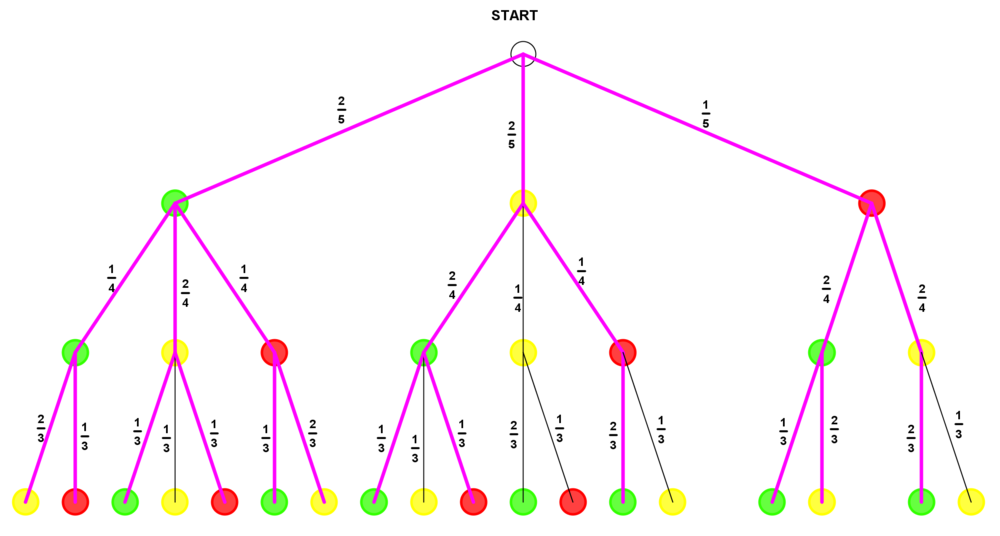
Die Möglichkeiten, höchstens ein gelbes Gummibärchen zu ziehen, sind im folgenden Baumdiagramm dargestellt:

Berechnung der Wahrscheinlichkeit:

P(E₃) = P({grün;grün;gelb}) + P({grün;grün;rot}) + P({grün;gelb;grün}) + P({grün;gelb;rot}) + P({grün;rot;grün}) + P({grün;rot;gelb}) + P({gelb;grün;grün}) + P({gelb;grün;rot}) +

+ P({gelb;rot;grün}) + P({rot;grün;grün}) + P({rot;grün;gelb}) + P({rot;gelb;grün}) =

= $\frac{2}{5}$ $\cdot$ $\frac{1}{4}$ $\cdot$ $\frac{2}{3}$ + $\frac{2}{5}$ $\cdot$ $\frac{1}{4}$ $\cdot$ $\frac{2}{3}$ + $\frac{2}{5}$ $\cdot$ $\frac{2}{4}$ $\cdot$ $\frac{1}{3}$ + $\frac{2}{5}$ $\cdot$ $\frac{2}{4}$ $\cdot$ $\frac{1}{3}$ + $\frac{2}{5}$ $\cdot$ $\frac{1}{4}$ $\cdot$ $\frac{1}{3}$ + $\frac{2}{5}$ $\cdot$ $\frac{1}{4}$ $\cdot$ $\frac{2}{3}$ + $\frac{2}{5}$ $\cdot$ $\frac{2}{4}$ $\cdot$ $\frac{1}{3}$ + $\frac{2}{5}$ $\cdot$ $\frac{2}{4}$ $\cdot$ $\frac{1}{3}$ + $\frac{2}{5}$ $\cdot$ $\frac{1}{4}$ $\cdot$ $\frac{2}{3}$ +

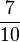+ $\frac{1}{5}$ $\cdot$ $\frac{2}{4}$ $\cdot$ $\frac{1}{3}$ + $\frac{1}{5}$ $\cdot$ $\frac{2}{4}$ $\cdot$ $\frac{2}{3}$ + $\frac{1}{5}$ $\cdot$ $\frac{2}{4}$ $\cdot$ $\frac{2}{3}$ = $\frac{7}{10}$ = 70%

$\Leftarrow$ Zurück

Version vom 28. September 2009, 00:59 Uhr (Quelltext anzeigen) Annalena Dürr (Diskussion \| Beiträge) K ← Zum vorherigen Versionsunterschied		Version vom 28. September 2009, 01:03 Uhr (Quelltext anzeigen) Annalena Dürr (Diskussion \| Beiträge) K Zum nächsten Versionsunterschied →
Zeile 15:		Zeile 15:


−	+ <math>\frac{1}{5}</math> <math>\cdot</math> <math>\frac{2}{4}</math> <math>\cdot</math> <math>\frac{1}{3}</math> + <math>\frac{1}{5}</math> <math>\cdot</math> <math>\frac{2}{4}</math> <math>\cdot</math> <math>\frac{2}{3}</math> + <math>\frac{1}{5}</math> <math>\cdot</math> <math>\frac{2}{4}</math> <math>\cdot</math> <math>\frac{2}{3}</math> = <math>\frac{3}{5}</math> = 60%	+	+ <math>\frac{1}{5}</math> <math>\cdot</math> <math>\frac{2}{4}</math> <math>\cdot</math> <math>\frac{1}{3}</math> + <math>\frac{1}{5}</math> <math>\cdot</math> <math>\frac{2}{4}</math> <math>\cdot</math> <math>\frac{2}{3}</math> + <math>\frac{1}{5}</math> <math>\cdot</math> <math>\frac{2}{4}</math> <math>\cdot</math> <math>\frac{2}{3}</math> = <math>\frac{7}{10}</math> = 70%



	<div align="left">[[Zusammengesetzte Zufallsexperimente und Pfadregeln\|<math>\Leftarrow</math> Zurück]]</div>		<div align="left">[[Zusammengesetzte Zufallsexperimente und Pfadregeln\|<math>\Leftarrow</math> Zurück]]</div>

Lösungsvorschlag iii): Unterschied zwischen den Versionen

Version vom 28. September 2009, 01:03 Uhr

Navigationsmenü

Meine Werkzeuge

Namensräume

Varianten

Ansichten

Aktionen

Suche

Navigation

Werkzeuge