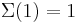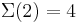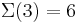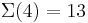Prinzipielle Grenzen der Berechenbarkeit: Unterschied zwischen den Versionen
K |
K |
||
| Zeile 108: | Zeile 108: | ||
* usw. | * usw. | ||
| − | Diese Art der Kodierung ist eher von theoretischer Bedeutung, weil man sehr schnell extrem große Zahlen erhält. Das obige Beispiel ergäbe ausmultipliziert <math> | + | Diese Art der Kodierung ist eher von theoretischer Bedeutung, weil man sehr schnell extrem große Zahlen erhält. Das obige Beispiel ergäbe ausmultipliziert <math>4 295755 033035 330312 782822 373101 172263 241726 791467 766561 298496 119787 168861 226939 162111 091690 789226 678438 109832 000000</math> (eine 115-stellige Zahl). Es ist auch ziemlich aufwändig diese Zahlen in Primfaktoren zu zerlegen. Aus diesem Grund sind große Primzahlen für die Verschlüsselungstechnik so wichtig. |
}} | }} | ||
}} | }} | ||
Version vom 30. September 2009, 16:12 Uhr
|
Lernpfad
|
Algorithmus
Übernehme die Definition in deinen Laufzettel!
Definition
Ein Algorithmus ist eine Verarbeitungsvorschrift, die aus einer endlichen Folge von eindeutig ausführbaren Anweisungen besteht, die aus endlich vielen Eingabedaten endlich viele Ausgabedaten erzeugt und mit der man eine Vielzahl gleichartiger Aufgaben lösen kann.
Wie du sicher bemerkt hast, kommt in dieser Definition sehr oft der Begriff "endlich" vor. Dies wird später noch eine entscheidende Rolle spielen!
Welche Aufgaben lassen sich mit einem Algorithmus umsetzen? (Lösen einer quadratischen Gleichung) (!Auflistung aller Primzahlen) (Auflistung aller Primzahlen kleiner als 300000) (Konstruieren eines Kreises durch 3 Punkte, die nicht auf einer Gerade liegen) (Wechseln eines Autoreifens) (!Schreiben einer Eins in der Schulaufgabe)
Schreibe deine Antworten auf deinen Laufzettel, bevor du in der Lösung nachsiehst.
Lösung:
- Eine quadratische Gleichung lässt sich immer in folgender Form schreiben:
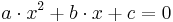 . Mittels der Mitternachtsformel
. Mittels der Mitternachtsformel 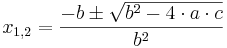 erhält man dann die Lösungen.
erhält man dann die Lösungen.
- Ein Kreis durch 3 Punkte A,B,C die nicht auf einer Gerade liegen lässt sich folgendermaßen Konstruieren: 1) Verbinde die Punkt A und B, sowie B und C mit einer Strecke. 2) Konstruiere die Mittelsenkrechten der Strecken [AB] und [BC]. 3) Der Schnittpunkt M der beiden Mittelsenkrechten von [AB] und [BC] ist der Mittelpunkt des Kreises durch die Punkte A,B und C. 4) Zeichne den Kreis mit Mittelpunkt M und Radius [MA]. Siehe auch hier.
- Das Wechseln eines Autoreifens folgendermaßen bewerkstelligen: 1) Stelle den Wagenheber unter die Markierung für den zu wechselnden Reifen. 2) Betätige den Wagenheber, so dass der Reifen entlastet wird, aber immer noch Bodenkontakt hat. 3) Lockere die Radmuttern mit Hilfe des Radkreuzes durch Drehen gegen den Uhrzeigersinn, aber schraube die Radmuttern nicht ganz ab. 4) Betätige den Wagenheber weiter, so dass der Reifen keinen Bodenkontakt mehr hat. 5) Ziehe den Reifen vorsichtig ab, so dass das Auto nicht vom Wagenheber rutscht. 6)Führe die Schritte 1-5 in umgekehrter Reihenfolge und umgekehrter Drehrichtung mit dem neuen Reifen durch.
- Ein Auflistung aller Primzahlen ist nicht möglich, da es unendlich viele davon gibt. Dies widerspricht der Definition eines Algorithmus, dass er endlich viele Ausgabedaten erzeugt.
- Die Auflistung alles Primzahlen kleiner als 300000 ist aber z.B. mit dem Sieb des Eratosthenes möglich, da es eine feste Anzahl ist.
- Das Schreiben einer Eins ist leider nicht möglich, sonst könnte man in jedem Fach ohne große Probleme eine Eins haben.
Gödelisierung
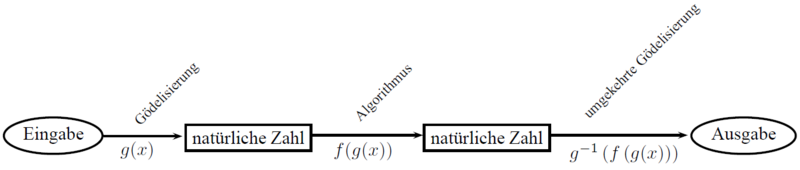
Wir versuchen jetzt Hilfe von der Mathematik zu erhalten. Dazu wandelt man Probleme in eine Form um, die es erlaubt, Wissen über Abbildungen innerhalb der natürlichen Zahlen zu benutzen. Um dies zu erreichen, wandelt man die Ein- und Ausgabedaten in natürliche Zahlen um.
|
Die 26 Buchstaben des Alphabets werden mit den Zahlen 1 bis 26 kodiert. Damit könnte man ein geschriebenes Wort als Zahl schreiben. Dekodiere die Zahl "26235945212097"! Welche Buchstabenfolge erhält man nach dem Dekodieren? Übernehme das dekodierte Wort in deinen Laufzettel.
Möglichkeiten für das dekodierte Wort sind z.B.: ZWEIDEUTIG oder BFBCEIDEBATIG oder ..., da man nicht weiß, ob z.B. 26 als Z oder als BF interpretiert werden soll.
|
|
Nun werden die 26 Buchstaben des Alphabets mit den Zahlen 01 bis 26 kodiert. Schreibt man die kodierten Buchstaben hintereinander, so erhält man eine Zahl. Dekodiere die Zahl "26230509060512121519". Übernehme das dekodierte Wort in deinen Laufzettel.
Das dekodierte Wort lautet: ZWEIFELLOS
|
Jetzt wird es etwas schwieriger. Diese Aufgabe musst du dir genau durchlesen. Vielleicht auch mehrmals. Solltest du nicht auf die Lösung kommen, kannst du dir die versteckte Lösung anschauen.
|
Nun werden die 26 Buchstaben des Alphabets wie folgt kodiert: Den 26 Buchstaben des Alphabets wird jeweils eine eindeutige Zahl zwischen 1 und 26 zugeordnet. Ein Wort wird nun mit fortlaufenden Primzahlpotenzen kodiert, also wenn a die Zahl 1, b die Zahl 2, c die Zahl 3 zugeordnet wird, dann wird das Wort abbca wie folgt kodiert:
Multipliziert man diese Zahlen miteinander, erhält man die Zahl Welche Buchstabenfolge erhält man, wenn man die Zahl " Übernehme das dekodierte Wort auf deinen Laufzettel. Falls du nicht auf die Lösung gekommen bist, notiere auf dem Laufzettel Wort "zu schwer" und lies dir die Lösung durch.
Das dekodierte Wort lautet: INFORMATIK.
Diese Art der Kodierung ist eher von theoretischer Bedeutung, weil man sehr schnell extrem große Zahlen erhält. Das obige Beispiel ergäbe ausmultipliziert
|
Mit einer Gödelisierung lassen sich beliebige Ein- und Ausgaben in natürliche Zahlen umwandeln und umgekehrt. Dies kann mehr oder minder geschickt erfolgen. Man kann sich dazu die verschiedensten Verfahren überlegen. Kurt Gödel hat sich mit solchen Fragestellungen beschäftigt, weshalb man entsprechende Verfahren nach ihm benannt hat. Diese Vorgehensweise wird häufig in der theoretischen Informatik verwendet, da sich Algorithmen dadurch als Funktionen über den natürlichen Zahlen abbilden lassen. Zur Umwandlung existieren verschiedenste Verfahren.
Definition
Eine Gödelisierung ist eine Abbildung 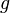 von der Menge der Ein- und Ausgaben
von der Menge der Ein- und Ausgaben 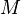 eines Algorithmus in die Menge der natürlichen Zahlen
eines Algorithmus in die Menge der natürlichen Zahlen 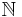 :
: 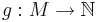 .
Die Abbildung muss dabei noch drei Bedingungen erfüllen:
.
Die Abbildung muss dabei noch drei Bedingungen erfüllen:
-
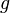 muss injektiv sein, d.h. jede natürliche Zahl darf höchstens das Bild von einem Programm sein; aber nicht jede natürliche Zahl muss auch ein Programm sein.
muss injektiv sein, d.h. jede natürliche Zahl darf höchstens das Bild von einem Programm sein; aber nicht jede natürliche Zahl muss auch ein Programm sein. 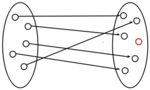
- Die Bildmenge muss entscheidbar sein, es muss also einen Algorithmus geben, der Ja ausgibt, wenn die Zahl einer gültigen Ein- oder Ausgabe entspricht und Nein, wenn es keine ist.
- Die Umkehrfunktion
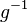 muss berechenbar sein, d.h. man muss aus der natürlichen Zahl auch wieder die zugehörige Ein- oder Ausgabe bekommen können.
muss berechenbar sein, d.h. man muss aus der natürlichen Zahl auch wieder die zugehörige Ein- oder Ausgabe bekommen können.
Welches der obigen Verfahren eignet sich für eine Gödelisierung? (!Kodierung mit Zahlen 1 bis 26) (Kodierung mit Zahlen 01 bis 26) (Kodierung mit Primzahlpotenzen)(!Keines der Verfahren)
Übernehme deine Antworten auf den Laufzettel.
Notiere diesen Merksatz auf deinem Laufzettel.
30px Merke
Durch das Verfahren der Gödelisierung kann man jeden Algorithmus als eine Abbildung von einer natürlichen Zahl auf eine andere ansehen. |
Wie viele Algorithmen gibt es?
Wie bei der Definition des Begriffes Algorithmus bereits erwähnt wurde, ist der Begriff der Endlichkeit von großer Bedeutung. Da ein Algorithmus eine endliche Folge von Anweisungen ist, besteht ein Algorithmus auch nur aus endlich vielen Zeichen. Mit der oben beschriebenen Gödelisierung lässt sich also jeder Algorithmus auch als eine eindeutige natürliche Zahl auffassen. Weil dann die Menge aller Algorithmen eine Teilmenge der natürlichen Zahlen ist, sind die Algorithmen abzählbar, man kann die Algorithmen also durchnummerieren.
Durch die Gödelisierung kann man die Algorithmen als Funktionen natürlicher Zahlen ansehen. Wir schreiben die Algorithmen und die möglichen Eingaben als eine unendlich große zweidimensionale Tabelle auf. An der Seite werden die Algorithmen bzw. die Funktionen der Reihe nach angetragen und als Spaltenüberschriften werden die möglichen Eingaben als Gödelnummer angetragen:
| 1 | 2 | 3 | 4 | 5 | ... | |
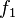 |
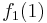 |
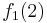 |
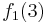 |
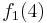 |
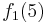 |
... |
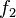 |
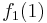 |
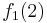 |
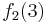 |
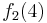 |
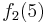 |
... |
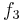 |
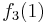 |
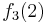 |
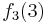 |
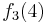 |
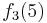 |
... |
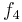 |
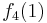 |
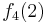 |
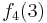 |
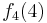 |
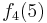 |
... |
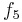 |
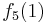 |
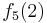 |
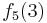 |
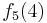 |
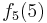 |
... |
| ... | ... | ... | ... | ... | ... | ... |
Diese Tabelle enthält alle algorithmisierbaren Funktionen. In der ersten Zeile stehen alle Funktionswerte der Funktion 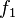 , in der zweiten Zeile stehen alle Funktionswerte der Funktion
, in der zweiten Zeile stehen alle Funktionswerte der Funktion 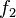 usw.
usw.
Wir definieren uns nun eine Funktion 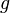 wie folgt:
wie folgt:
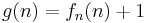
Diese Funktion ist offensichtlich berechenbar, also müsste sie irgendwo in der Folge 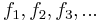 vorkommen. Wir nehmen an, dass es die Funktion mit der Nummer
vorkommen. Wir nehmen an, dass es die Funktion mit der Nummer  ist, also
ist, also 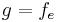 . Wir erhalten aus der Definition von
. Wir erhalten aus der Definition von 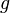 , dass
, dass 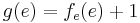 ist, aber aus
ist, aber aus 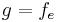 folgt, dass
folgt, dass 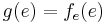 gilt. Es soll also
gilt. Es soll also 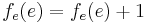 sein. Das kann aber nicht sein. Also haben wir einen Widerspruch gefunden und die Funktion
sein. Das kann aber nicht sein. Also haben wir einen Widerspruch gefunden und die Funktion 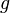 kann kein Algorithmus sein!
kann kein Algorithmus sein!
Damit haben wir eine Funktion gefunden, für die kein Algorithmus existieren kann!
Notiere diesen Merksatz auf deinen Laufzettel.
30px Merke
|
Beispiele für Probleme, die nicht algorithmisch lösbar sind:
- Fermatsche Vermutung: Es gibt keine natürlichen Zahlen
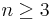 , für die positive ganze Zahlen
, für die positive ganze Zahlen 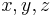 existieren mit
existieren mit 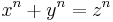 . Erst 1994 konnte Andrew Wiles diese Vermutung mit einem 100seitigen Beweis bestätigen.
. Erst 1994 konnte Andrew Wiles diese Vermutung mit einem 100seitigen Beweis bestätigen.
- Goldbachsche Vermutung: Jede gerade Zahl
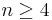 lässt sich als Summe von zwei Primzahlen darstellen. Diese Vermutung konnte bis heute weder bewiesen noch widerlegt werden.
lässt sich als Summe von zwei Primzahlen darstellen. Diese Vermutung konnte bis heute weder bewiesen noch widerlegt werden.
- Gibt es unendliche viele Primzahlzwilligen (zwei Primzahlen, die eine Differenz von 2 haben)? Diese Frage konnte bis heute nicht entschieden werden.
Turing-Maschine
Bisher haben wir uns bei der Programmierung von Algorithmen immer auf eine Programmiersprache beschränkt (Java, C, C++, C#, VisualBasic, Pascal,...). Nun stellt sich die Frage, ob die eine Programmiersprache mehr kann als die andere.
Der englische Mathematiker Alan Turing hat dazu mit seinem Modell der Turingmaschine einen entscheidenden Teil dazu beigetragen. Er entwickelte dazu ein mathematisches Modell, das das systematische Vorgehen des Menschen z.B. bei der Addition nachbildet. Man benötigt dazu einen Bleistift, ein Rechenblatt und einen Radiergummi. Auf dem Rechenblatt werden die Rechnungen sowie alle Rechenergebnisse aufgeschrieben. Mit dem Bleistift kann man einzelne Zeichen auf das Blatt schreiben und mit dem Radiergummi auch wieder löschen. Die Aktion, die man ausführt hängt nur von den endlich vielen Zeichen auf dem Rechenblatt ab. Die Berechnung selbst wird durch eine Berechnungsvorschrift gesteuert.
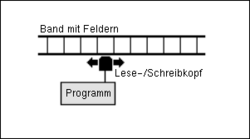
Die Turingmaschine enthält deswegen folgenden Komponenten:
- ein unendlich langes Speicherband mit unendlich vielen Feldern. In jedem dieser Felder ist genau ein Zeichen gespeichert. Dabei ist als Zeichen ein Blanksymbol (Leerzeichen) zugelassen, was so viel bedeutet wie „leeres Feld“. Das Blanksymbol gehört nicht zu der Menge der Eingabezeichen. Zur Vereinfachung der Vorstellung kann man sich auch ein endliches Band vorstellen. Dieses muss dann nur lang genug sein, damit die Berechnungen ausgeführt werden können.
- ein Schreib-/Lesekopf, der ein Zeichen aus dem aktuellen Feld lesen und hineinschreiben kann, sowie seine Position ein Feld nach links oder rechts bewegen kann.
- einen internen Zustand
Je nach Zustand, in dem sich die Turing-Maschine befindet, kann sie ein Zeichen auf das Band schreiben, den Schreib-/Lesekopf um ein Feld nach links oder rechts bewegen und den internen Zustand ändern.
Übertrage das Schaubild der Turingmaschine auf deinen Laufzettel.
Eine mathematisch exakte Definition einer Turing-Maschine ist dann wie folgt:
Definition
Eine Turingmaschine ist gegeben durch das 7-Tupel 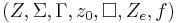 mit
mit
- einer endliche Zustandsmenge
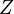
- einer endliche Menge an Eingabezeichen
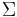
- einer Menge an zulässigen Bandzeichen
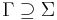 (die Menge der Eingabezeichen ist eine Teilmenge der zulässigen Bandzeichen)
(die Menge der Eingabezeichen ist eine Teilmenge der zulässigen Bandzeichen)
- einem Startzustand
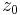
- dem Blank-Symbol

- einer Menge an Endzuständen
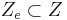
- einer Überführungsfunktion
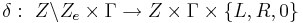 (L
(L  Schreib-/Lesekopfbewegung nach links, R
Schreib-/Lesekopfbewegung nach links, R  Schreib-/Lesekopfbewegung nach rechts, 0
Schreib-/Lesekopfbewegung nach rechts, 0  keine Schreib-/Lesekopfbewegung)
keine Schreib-/Lesekopfbewegung)
Hier findet ihr noch eine Turing-Maschinen-Simulator als Java-Anwendung (Java Runtime Environment 1.5 oder höher muss installiert sein):
(Quelle: [1]. Dort findet sich auch eine Dokumentation)
Um den Simulator zu nutzen, musst du diesen herunterladen und auf deinem Rechner entpacken und anschließend die Datei alan-1.0.jar öffnen. Durch anklicken des Ordner-Symboles kann man vorgefertigte Turingprogramme laden und ausführen. Die Anfangskonfiguration kann man im Feld "Tape Start" angeben. Mit einem Klick auf das Play-Symbol startet die Maschine mit der Ausführung des Programms. Selbstverständlich kannst du auch eigene Programme erstellen und speichern und ausführen. Nähere Informationen findest du in der beigelegten PDF-Datei.
In dieser Tabelle ist die Überführungsfunktion einer Turingmaschine zu finden, die zwei Binärzahlen addieren kann. Die Eingabe muss dann in der Form 110+111 auf dem Band stehen.
| Zustand | lesen | schreiben | Kopfbewegung | neuer Zustand |
|---|---|---|---|---|
| 0 | 0 | 0 | r | 1 |
| 0 | 1 | 1 | r | 1 |
| 1 | 0 | 0 | r | 1 |
| 1 | 1 | 1 | r | 1 |
| 1 | N | N | r | 1 |
| 1 | E | E | r | 1 |
| 1 | + | + | r | 1 |
| 1 | * | * | l | 2 |
| 2 | 0 | * | l | 3 |
| 2 | 1 | * | l | 10 |
| 2 | + | * | l | 20 |
| 3 | 0 | 0 | l | 3 |
| 3 | 1 | 1 | l | 3 |
| 3 | + | + | l | 4 |
| 4 | N | N | l | 4 |
| 4 | E | E | l | 4 |
| 4 | 0 | N | r | 1 |
| 4 | 1 | E | r | 1 |
| 4 | * | N | r | 1 |
| 10 | 0 | 0 | l | 10 |
| 10 | 1 | 1 | l | 10 |
| 10 | + | + | l | 11 |
| 11 | N | N | l | 11 |
| 11 | E | E | l | 11 |
| 11 | 0 | E | r | 1 |
| 11 | 1 | N | l | 12 |
| 11 | * | E | r | 1 |
| 12 | 0 | 1 | r | 1 |
| 12 | 1 | 0 | l | 12 |
| 12 | * | 1 | r | 1 |
| 20 | N | 0 | l | 20 |
| 20 | E | 1 | l | 20 |
| 20 | 0 | 0 | l | 20 |
| 20 | 1 | 1 | l | 20 |
|
Du kannst zum Probieren auch den oben vorgestellten Turing-Simulator benutzen.
Ein mögliches Programm könnte folgendermaßen aussehen: # entspricht dem Leerzeichen z0,# -> z1,#,R z1,1 -> z2,#,R z2,1 -> z2,1,R z2,+ -> z2,1,R z2,# -> z3,#,0 z3 ist der Endzustand Dieses Programm geht zuerst zu der ersten 1 nach rechts, ersetzt sie durch ein Leerzeichen, geht weiter nach rechts, bis es das + findet, ersetzt das + durch eine 1 und läuft weiter nach rechts bis es das nächste Leerzeichen findet und stoppt. Auf dem Band steht dann die Summe der beiden Unärzahlen.
|
Churchsche These
Warum befassen wir uns mit Turing-Maschinen? Das Modell der Turing-Maschinen ist die erste exakte Präzisierungen des Begriffs "Algorithmus" gewesen, d.h. jede berechenbare Funktion kann durch eine Turing-Maschine realisiert werden. Umgekehrt repräsentiert jede Turing-Maschine eine berechenbare Funktion. Das ist der Grund, warum sich die theoretische Informatik mit Turing-Maschinen beschäftigt.
Notiere die Churchsche These auf deinem Laufzettel.
30px Merke
These von Church Jede im intuitiven Sinne berechenbare Funktion ist auch turing-berechenbar, d.h. man kann eine Turing-Maschine entwerfen, die diese Funktion berechnet. |
Diese These kann man natürlich nicht beweisen, da der Begriff "intuitiv berechenbar" nicht mathematisch präzisiert werden kann.
An der Station über Turing-Maschinen hast du bereits eine in Java realisierte Turing-Maschine kennen gelernt. Die Programmiersprache Java kann also mindestens genauso viele Programme realisieren wie eine Turing-Maschine. Es lässt sich aber auch zeigen, dass die Turing-Maschine genauso viel berechnen können wie z.B. Java.
Nicht berechenbare Probleme
Das Halteproblem
Die folgende Situation hast du vielleicht auch schon erlebt:
Du hast ein tolles Programm geschrieben und willst es einem Freund oder einer Freundin zeigen. Du startest das Programm mit einer zuvor nicht getesteten Eingabe. Ihr beide sitzt vor dem Bildschirm und der Rechner rechnet und rechnet.
Jetzt stellt sich die Frage ob das Programm soviel Zeit benötigt, weil die Berechnung so komplex ist oder befindet sich das Programm in einer Endlosschleife?
An dieser Stelle wünscht man sich ein Programm, dem man das eigene Programm übergibt und das dann ein "Ja" ausgibt, falls unser Programm für alle möglichen Eingaben anhält, oder "Nein", falls es eine Eingabe gibt, für die das Programm nicht anhält.
Kann es ein solches Haltetest-Programm geben?
Nehmen wir einmal an, es gibt ein solches Java-Programm. Der Quelltext sieht dann in etwa folgendermaßen aus:
class HalteTester{
static boolean esStoppt;
public static void main(String args []){
// hier wird das eingegebene Programm untersucht
// und je nach Ergebnis die Variable esStoppt gesetzt
if (esStoppt==true){
System.out.println("Das Programm ist selbststoppend.");
}
else System.out.println("Das Programm ist nicht selbststoppend.");
}
}
Wenn ein solches Programm "HalteTester" existiert, dann kann man auch folgendes Programm schreiben:
class Wundersam{
static boolean esStoppt;
public static void main(String args []){
// hier wird das eingegebene Programm untersucht
// und je nach Ergebnis die Variable esStoppt gesetzt,
// genau wie bei HalteTester.
if (esStoppt==true){
System.out.println("Das Programm ist selbststoppend.");
while(true) { /* Endlosschleife */ }
}
else System.out.println("Das Programm ist nicht selbststoppend.");
}
}
Das Programm "Wundersam" unterscheidet sich vom Programm "HalteTester" nur durch die eingebaute Endlosschleife. Ist das Programm "Wundersam" nun selbststoppend?
- Angenommen das Programm "Wundersam" ist selbststoppend. Dann wir zuerst der Testteil ausgeführt und die Variable "esStoppt" erhält den Wert "true", weil das Programm "Wundersam" nach Annahme selbststoppend ist. Anschließend wir der Text "Das Programm ist selbststoppend." ausgegeben und das Programm gerät in eine Endlosschleife. Das Programm wird also nicht stoppen. Dies ist ein Widerspruch dazu, dass das Programm selbststoppend ist.
- Nehmen wir jetzt an, dass das Programm "Wundersam" nicht selbststoppend ist. Dann wird wieder der Testteil ausgeführt und die Variable "esStoppt" erhält den Wert "false", weil das Programm nach Annahme nicht selbststoppend ist. Anschließend wird dann der Text "Das Programm ist nicht selbststoppend." ausgegeben und das Programm "Wundersam" stoppt. Dies ist ein Widerspruch dazu, dass das Programm nicht selbststoppend ist.
Wir haben jetzt die beiden Fälle untersucht, ob das Programm "Wundersam" stoppt oder nicht und sind zu keinem Ergebnis gekommen. Das Programm ist also gleichzeitig selbststoppend und nicht selbststoppend. Nach den Gesetzen der Logik kann es ein solches Programm "Wundersam" nicht geben. Dies hat zur Folge, dass es auch das Programm "HalteTester" nicht geben kann, da das Programm "Wundersam" aus dem Programm "HalteTester" konstruiert worden ist.
30px Merke
Damit ist bewiesen, dass es kein Java-Programm (und damit auch kein Programm in einer anderen Programmiersprache) gibt, mit dem man für jedes andere Java-Programm entscheiden kann, ob es bei beliebiger Eingabe anhält oder nicht. |
|
Kann es außer Endlosschleifen auch andere Gründe dafür geben, dass ein Programm nicht anhält?
Nein, es kann keinen anderen Grund dafür geben, denn ein Programm ist eine endliche Folge von Anweisungsblöcken, die in endlicher Zeit abgearbeitet sein muss, falls nicht mindestens einer der Anweisungsblöcke eine unendliche Folge von Einzelanweisungen ist.
|
Fleißige Biber
Als Abschluss wollen wir noch eine klar zu beschreibende und dennoch nicht berechenbare Aufgabe betrachten: Die Fleißigen Biber (engl. busy beaver).
Bei den Fleißigen Bibern geht es darum, eine Turing-Maschine mit 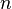 Zuständen (plus einem Endzustand) zu finden, die eine maximale Anzahl an Einsen auf das Band schreibt und dann stoppt.
Nun ist die Frage, wie viele Einsen das sind. Man bezeichnet diese Funktion auch als Radó-Funktion.
Zuständen (plus einem Endzustand) zu finden, die eine maximale Anzahl an Einsen auf das Band schreibt und dann stoppt.
Nun ist die Frage, wie viele Einsen das sind. Man bezeichnet diese Funktion auch als Radó-Funktion.
Überlegen wir uns einmal, wie viele verschiedene Turingmaschinen man mit 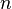 Zuständen "bauen" kann.
Zuständen "bauen" kann.
Die Überführungsfunktion einer solchen Turingmaschine ist dann wie folgt definiert:
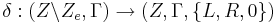
Dabei ist
-
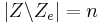 (Anzahl der Nicht-Endzustände)
(Anzahl der Nicht-Endzustände)
-
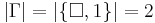 (Anzahl der Buchstaben des Bandalphabets)
(Anzahl der Buchstaben des Bandalphabets)
-
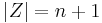 (Anzahl aller Zustände incl. Endzustand)
(Anzahl aller Zustände incl. Endzustand)
-
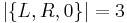 (Anzahl der möglichen Bandbewegungen).
(Anzahl der möglichen Bandbewegungen).
Die Definitionsmenge der Überführungsfunktion hat dann also
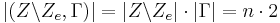 Elemente und die Zielmenge
Elemente und die Zielmenge
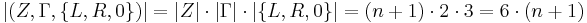 Elemente.
Elemente.
Man weiß, dass die Anzahl der Abbildungen zwischen zwei Mengen 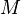 mit
mit 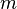 Elementen und
Elementen und 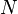 mit
mit 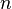 Elementen gleich
Elementen gleich 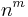 ist.
ist.
Die Anzahl der möglichen Turing-Maschinen ist dann die Anzahl der Abbildungen zwischen 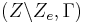 und
und 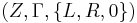 . Dies sind gerade
. Dies sind gerade 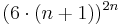
Damit erhält man in Abhängigkeit von 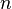 folgende Anzahl an Turingmaschinen:
folgende Anzahl an Turingmaschinen:
| n (Anzahl der Zustände) |
N (Anzahl der Turingmaschinen) |
|---|---|
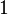 |
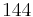
|
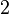 |
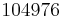
|
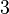 |
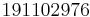
|
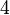 |
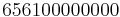
|
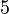 |
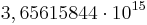
|
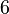 |
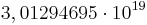
|
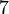 |
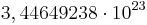
|
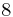 |
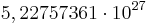
|
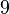 |
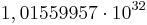
|
| ... | ... |
Man kann also erkennen, dass die Anzahl der Turing-Maschinen, die man untersuchen muss extrem schnell ansteigt. Aus diesem Grund kennt man auch erst die ersten 4 Werte der Radó-Funktion 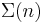 . Diese sind:
. Diese sind:
Für alle größeren 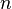 gibt es nur Schätzungen. Von
gibt es nur Schätzungen. Von 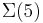 weiß man nur, dass der Wert mindestens 4096 ist, d.h. eine Turingmaschine mit 5 Zuständen kann mindestens 4096 Einsen auf ein leeres Band schreiben, eine Turing-Maschine mit 6 Zuständen sogar mindestens 95524079 Einsen. Der Grund dafür, dass man keine genaue Zahl angeben kann, ist, dass man alle möglichen Turing-Maschinen testen muss, ob sie anhalten oder nicht. Wenn eine Turing-Maschine anhält, weiß man, wie viele Einsen sie auf das Band geschrieben hat. Hält eine Turing-Maschine allerdings nicht an, muss man noch beweisen, dass sie nicht anhält.
weiß man nur, dass der Wert mindestens 4096 ist, d.h. eine Turingmaschine mit 5 Zuständen kann mindestens 4096 Einsen auf ein leeres Band schreiben, eine Turing-Maschine mit 6 Zuständen sogar mindestens 95524079 Einsen. Der Grund dafür, dass man keine genaue Zahl angeben kann, ist, dass man alle möglichen Turing-Maschinen testen muss, ob sie anhalten oder nicht. Wenn eine Turing-Maschine anhält, weiß man, wie viele Einsen sie auf das Band geschrieben hat. Hält eine Turing-Maschine allerdings nicht an, muss man noch beweisen, dass sie nicht anhält.
Selbst für kleinere Zustandszahlen wie 5 oder 6 ist es nicht mehr möglich alle möglichen Turingmaschinen zu überprüfen. Angenommen wir hätten einen Computer, der in einer Sekunde für 1 Million Turing-Maschinen überprüfen kann, ob sie halten (es müsste einen Computer geben, der das Halteproblem lösen kann) und wenn ja, wie viele Einsen sie auf das leere Band schreiben kann, würde dies für 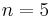 bereits über 115 Jahre dauern.
bereits über 115 Jahre dauern.
|
Schreibe einen fleißigen Biber mit einem Zustand plus Endzustand der genau eine 1 auf das leere Band schreibt und dann stoppt.
Ein Turing-Programm mit einem Zustand plus Endzustand, das eine 1 auf das Band schreibt, sieht folgendermaßen aus: # entspricht dem Leerzeichen, z1 ist der Endzustand z0,# -> z1, 1, R
|
|
Schreibe einen fleißigen Biber mit zwei Zuständen plus Endzustand der genau vier 1en auf das leere Band schreibt und dann stoppt.
Ein Turing-Programm mit zwei Zuständen plus Endzustand, das eine 1111 auf das Band schreibt, sieht folgendermaßen aus: # entspricht dem Leerzeichen, z3 ist der Endzustand z0,# -> z1, 1, L z0,1 -> z2, 1, R z1,# -> z0, 1, R Z1,1 -> z3, 1, R
|
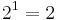 kodiert.
kodiert.
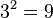 kodiert.
kodiert.
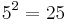 kodiert.
kodiert.
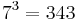 kodiert.
kodiert.
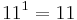 kodiert.
kodiert.
 .
Da die Primfaktorzerlegung eindeutig ist, wenn man die Primzahlpotenzen aufsteigend ordnet, kann man aus jeder Zahl das zugehörige Wort erzeugen.
.
Da die Primfaktorzerlegung eindeutig ist, wenn man die Primzahlpotenzen aufsteigend ordnet, kann man aus jeder Zahl das zugehörige Wort erzeugen.
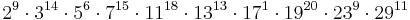 " dekodiert?
" dekodiert?
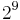 entspricht I (1. Primzahl bedeutet 1. Buchstabe des Wortes und 9. Buchstabe des Alphabets)
entspricht I (1. Primzahl bedeutet 1. Buchstabe des Wortes und 9. Buchstabe des Alphabets)
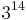 entspricht N (2. Primzahl bedeutet 2. Buchstabe des Wortes und 14. Buchstabe des Alphabets)
entspricht N (2. Primzahl bedeutet 2. Buchstabe des Wortes und 14. Buchstabe des Alphabets)
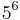 entspricht F (3. Primzahl bedeutet 3. Buchstabe des Wortes und 6. Buchstabe des Alphabets)
entspricht F (3. Primzahl bedeutet 3. Buchstabe des Wortes und 6. Buchstabe des Alphabets)
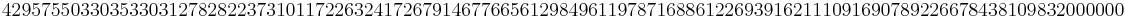 (eine 115-stellige Zahl). Es ist auch ziemlich aufwändig diese Zahlen in Primfaktoren zu zerlegen. Aus diesem Grund sind große Primzahlen für die Verschlüsselungstechnik so wichtig.
(eine 115-stellige Zahl). Es ist auch ziemlich aufwändig diese Zahlen in Primfaktoren zu zerlegen. Aus diesem Grund sind große Primzahlen für die Verschlüsselungstechnik so wichtig.
 getrennte Zahlen in Unärdarstellung (die Zahl
getrennte Zahlen in Unärdarstellung (die Zahl