Dose: Unterschied zwischen den Versionen
K (Änderung Maße und Runden hinzugefügt) |
K (Sprache) |
||
| (3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 33: | Zeile 33: | ||
(Runde auf eine ganze Zahl!) | (Runde auf eine ganze Zahl!) | ||
<br> | <br> | ||
| − | Die Dose muss | + | Die Grundfläche ist '''21''' cm<sup>2</sup> groß. |
| + | <br> | ||
| + | Die Dose muss '''12''' cm hoch sein. | ||
<br> | <br> | ||
<br> | <br> | ||
| Zeile 52: | Zeile 54: | ||
</span> | </span> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
<br> | <br> | ||
<br> | <br> | ||
Aktuelle Version vom 22. Oktober 2009, 18:23 Uhr
Eine Getränkefirma möchte für ihr neues Getränk eine ausgefallene Dose entwickeln.
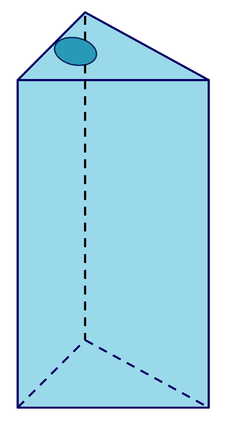
Ihr Designer rät ihnen zu einer Dose in Form eines Dreiecksprismas und macht sogleich Entwürfe.
Die Grundfläche der Dose ist ein gleichseitiges Dreieck.
Zum Lösen der Aufgaben musst du Milliliter in Kubikzentimeter umrechnen.
Wenn du dir nicht mehr ganz sicher bist, schaue in deiner Formelsammlung nach!
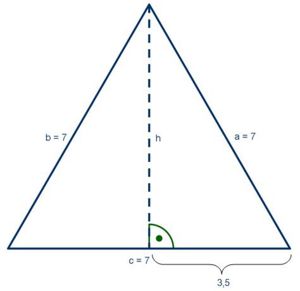
Entnimm die Maße für die folgenden Aufgaben bitte aus dem linken Bild!
1. Berechne die Höhe des gleichseitigen Dreiecks.
Die Höhe des Dreieck beträgt 6 cm.
2. Wie hoch muss die Dose werden, damit sie 250 ml fassen kann?
(Runde auf eine ganze Zahl!)
Die Grundfläche ist 21 cm2 groß.
Die Dose muss 12 cm hoch sein.
3. Wie viel Zentimeter höher ist die Dose, wenn sie 330 ml fassen soll ?
(Runde auf eine ganze Zahl!)
Die Dose ist 4 cm höher, also 16 cm hoch.
4. Die Getränkefirma entscheidet sich für die 250 ml-Dose.
Wie viel cm2 Weißblech wird für das Herstellen einer 250 ml-Dose benötigt?
(Hinweis: Ohne Berücksichtigung der Öffnung und des Verschnitts!)
Zum Herstellen der Dose braucht die Firma 294 cm2 Weißblech.
 Zurück zur vorherigen Aufgabe
Zurück zur vorherigen Aufgabe Weiter zur nächsten Aufgabe
Weiter zur nächsten Aufgabe
