Multiplikation von Brüchen/Station 2: Unterschied zwischen den Versionen
| (8 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
</div> | </div> | ||
<br> | <br> | ||
| + | <div style="border: 2px solid yellow; background-color:#ffffff; padding:7px;"> | ||
{{Merke|'''Multiplikation zweier Brüche''' <br> | {{Merke|'''Multiplikation zweier Brüche''' <br> | ||
* Zwei Brüche werden miteinander multipliziert, indem man den '''Zähler mit Zähler''' und den '''Nenner mit dem Nenner''' '''multipliziert''' | * Zwei Brüche werden miteinander multipliziert, indem man den '''Zähler mit Zähler''' und den '''Nenner mit dem Nenner''' '''multipliziert''' | ||
| Zeile 12: | Zeile 13: | ||
*allgemein: <math> \frac{a}{b} </math> * <math> \frac{c}{d} = \frac{a*c}{b*d} </math> = | *allgemein: <math> \frac{a}{b} </math> * <math> \frac{c}{d} = \frac{a*c}{b*d} </math> = | ||
| + | </div> | ||
| + | <br> | ||
Die folgenden Aufgaben sollen dir zeigen, ob du die Regel verstanden hast und es anwenden kannst: | Die folgenden Aufgaben sollen dir zeigen, ob du die Regel verstanden hast und es anwenden kannst: | ||
| − | + | <br> | |
| − | + | <div style="border: 2px solid red; background-color:#ffffff; padding:7px;"> | |
| − | Berechne nun die folgenden Aufgaben und schreibe die Lösung auf deinen Laufzettel. | + | <big>'''Aufgabe 1:'''</big><br> |
| + | '''Berechne nun die folgenden Aufgaben und schreibe die Lösung auf deinen Laufzettel.''' | ||
(kürze die Lösung soweit wie möglich und wandle in einen gemischten Bruch um) | (kürze die Lösung soweit wie möglich und wandle in einen gemischten Bruch um) | ||
| Zeile 23: | Zeile 27: | ||
c) <math> \frac{4}{9} </math> * <math> \frac{6}{9} </math> = | c) <math> \frac{4}{9} </math> * <math> \frac{6}{9} </math> = | ||
| − | + | </div> | |
| + | <br> | ||
| + | <br> | ||
| + | <div style="border: 2px solid red; background-color:#ffffff; padding:7px;"> | ||
| + | <big>'''Aufgabe2:'''</big><br> | ||
| + | <br> | ||
Am nächsten Tag kommt Tom ganz erschöpft von der Schule heim und freut sich auf '''Orangensaft''', eine '''Tafel Schokolade''' und eine '''Käse-Pizza'''. | Am nächsten Tag kommt Tom ganz erschöpft von der Schule heim und freut sich auf '''Orangensaft''', eine '''Tafel Schokolade''' und eine '''Käse-Pizza'''. | ||
Bevor Tom Essen und Trinken begonnen hat, sahen die Lebensmittel noch so aus:<br> | Bevor Tom Essen und Trinken begonnen hat, sahen die Lebensmittel noch so aus:<br> | ||
| Zeile 44: | Zeile 53: | ||
b) [[Bild:Sandra_Hemrich_Schokolade2.jpg]] | b) [[Bild:Sandra_Hemrich_Schokolade2.jpg]] | ||
c) [[Bild:Sandra_Hemrich_Pizza3_neu.jpg]] | c) [[Bild:Sandra_Hemrich_Pizza3_neu.jpg]] | ||
| + | </div> | ||
Aktuelle Version vom 12. Dezember 2009, 16:22 Uhr
2.Station: Multiplikation zweier Brüche
 Merke
Multiplikation zweier Brüche
|
- allgemein:
* 
=
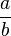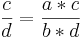Die folgenden Aufgaben sollen dir zeigen, ob du die Regel verstanden hast und es anwenden kannst:
Aufgabe 1:
Berechne nun die folgenden Aufgaben und schreibe die Lösung auf deinen Laufzettel.
(kürze die Lösung soweit wie möglich und wandle in einen gemischten Bruch um)
a)*
=
b)*
=
c)*
=
Aufgabe2:
Am nächsten Tag kommt Tom ganz erschöpft von der Schule heim und freut sich auf Orangensaft, eine Tafel Schokolade und eine Käse-Pizza.
Bevor Tom Essen und Trinken begonnen hat, sahen die Lebensmittel noch so aus:
Nachdem Tom gegessen und getrunken hat, blieb aber dennoch einiges übrig, denn sein Hunger und Durst war doch nicht so groß.
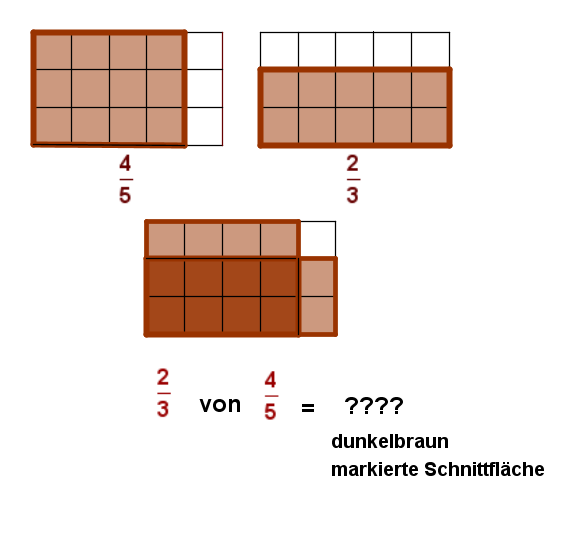
Du sollst nun die noch vorhandenen Lebensmittel als Bruch ausdrücken und dazu eine passenden Aufgabe finden, indem du zwei Brüche miteinander multiplizierst.
Schreibe deinen Lösungsvorschlag auf deinen Laufzettel!!!
Beispiel: Es bleiben noch einer Pizza übrig!!!
Die dazugehörige Aufgabe könnte dann lauten:*
Hier siehst du die übrig gebliebenen Reste von Tom:
a) 
b) 
c) 
