Aufgaben 7. Klasse/Dreiecke und Winkel/Seite 2: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
 
Zeile 45: Zeile 45:
  
 
w ist die Winkelhalbierende des Winkels δ.
 
w ist die Winkelhalbierende des Winkels δ.
 +
 +
<u>Hinweis:</u> Die Zeichnung ist nicht maßstabsgetreu!
  
  

Aktuelle Version vom 19. Januar 2010, 09:03 Uhr

Teilaufgabe b)

Um die Segel aber genauso bauen und zuschneiden zu können, benötigt Hans nun ein paar Winkelmaße. Der Strahl w ist die Winkelhalbierende des Winkels δ und der Winkel μ beträgt 120°

Bearbeite zuerst die Aufgabe rechts neben dem Applet!

Schiff Aufgabe


Schau dir zur Wiederholung vorher folgende Zeichnungen an.

Basiswinkel.png Stufenwinkel 2.png Nebenwinkel 2.png



1. ) Findest du entsprechende Winkel im Applet wieder? Versuche den Winkeln ihre Bezeichnungen zuzuordnen! Als Hilfe kannst du dir die Tipps "parallele Strecken" und "Dreieck" im Applet anschauen!

μ β α δ γ φ ε
Basiswinkel
Stufenwinkel
Nebenwinkel

Punkte: 0 / 0

2.) Toll gemacht! Fassen wir dies nun zusammen! Fülle dafür die folgenden Lücken aus!

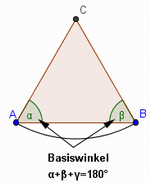
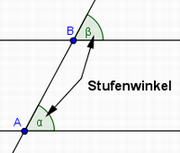
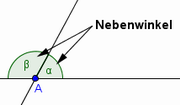
In einem Dreieck beträgt die Innenwinkelsumme180 (°). Basiswinkel und Stufenwinkel sind gleich groß (zwei Wörter) und Nebenwinkel ergänzen sich zu 180 (°).

3.) Jetzt bist du fit, um die Winkel zu berechnen!

Wenn du dir den Tipp "Anfang" im Applet anklickst, erscheint dir ein rotes Dreieck, mit dessen Winkel du bei deinen Berechnungen anfangen solltest!

w ist die Winkelhalbierende des Winkels δ.

Hinweis: Die Zeichnung ist nicht maßstabsgetreu!


α = 90(°)
β = 40(°)
γ = 100(°)
ε = 40(°)
δ = 40(°)
φ = 60(°)

→Schau dir hier die Teilaufgabe c) an

Von „http://dmuw.zum.de/index.php?title=Aufgaben_7._Klasse/Dreiecke_und_Winkel/Seite_2&oldid=13721“