Hilfe: Unterschied zwischen den Versionen
Aus DMUW-Wiki
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
<div style="border: 2px solid #0000ee; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid #0000ee; background-color:#ffffff; padding:7px;"> | ||
| − | '''''Sollst du entscheiden, ob ein | + | '''''Sollst du entscheiden, ob ein lineares Gleichungssystem eine, keine oder unendlich viele Lösungen hat, dann gehe so vor:''''' |
| Zeile 20: | Zeile 20: | ||
</center> | </center> | ||
|- | |- | ||
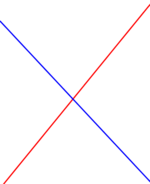
| − | | style="background-color:#FFFF00;" | '''1. Fall: Die Steigung ist verschieden. m<sub>1</sub> ungleich m<sub>2</sub>. ''' || style="background-color:#FFFF00 ;" | '''Ist die Steigung verschieden, dann | + | | style="background-color:#FFFF00;" | '''1. Fall: Die Steigung ist verschieden. m<sub>1</sub> ungleich m<sub>2</sub>. ''' || style="background-color:#FFFF00 ;" | '''Ist die Steigung verschieden, dann schneiden sich die Geraden und das lineare Gleichungssystem hat genau eine Lösung.''' [[Bild:Lernpfad_1_Station_5_Hatos_2.png|150px|center]] |
|- | |- | ||
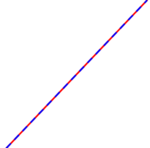
|style="background-color:#9AFF9A ;" | '''2. Fall: Die Steigung ist gleich. m<sub>1</sub> = m<sub>2</sub> aber die y- Achsenabschnitte sind verschieden. t<sub>1</sub> ungleich t<sub>2</sub>. ||style="background-color:#9AFF9A ;" | '''Wenn die Steigung gleich ist, aber die y - Achsenabschnitte verschieden sind, dann sind die Geraden paralell und es gibt keine Lösung!''' [[Bild:Lernpfad_1_Station_5_Hatos_1.png|200px|center]] | |style="background-color:#9AFF9A ;" | '''2. Fall: Die Steigung ist gleich. m<sub>1</sub> = m<sub>2</sub> aber die y- Achsenabschnitte sind verschieden. t<sub>1</sub> ungleich t<sub>2</sub>. ||style="background-color:#9AFF9A ;" | '''Wenn die Steigung gleich ist, aber die y - Achsenabschnitte verschieden sind, dann sind die Geraden paralell und es gibt keine Lösung!''' [[Bild:Lernpfad_1_Station_5_Hatos_1.png|200px|center]] | ||
Aktuelle Version vom 17. März 2010, 20:51 Uhr
Hilfestellung zu Station 6
Sollst du entscheiden, ob ein lineares Gleichungssystem eine, keine oder unendlich viele Lösungen hat, dann gehe so vor:
| Vorgehensweise |
Beispiel: y = m1 x + t1 und y - m2 x = t2 | ||||||
|---|---|---|---|---|---|---|---|
| Prüfe, ob beide Gleichungen in Normalform gegeben, also nach y aufgelöst sind. Ist das nicht der Fall, dann löse sie nach y auf. |
| ||||||
| 1. Fall: Die Steigung ist verschieden. m1 ungleich m2. | Ist die Steigung verschieden, dann schneiden sich die Geraden und das lineare Gleichungssystem hat genau eine Lösung. | ||||||
| 2. Fall: Die Steigung ist gleich. m1 = m2 aber die y- Achsenabschnitte sind verschieden. t1 ungleich t2. | Wenn die Steigung gleich ist, aber die y - Achsenabschnitte verschieden sind, dann sind die Geraden paralell und es gibt keine Lösung! | ||||||
| 3. Fall: Die Steigung ist gleich. m1 = m2 und die y- Achsenabschnitte sind auch gleich. t1 = t2 | Wenn die Steigung gleich ist und die y - Achsenabschnitte auch gleich sind, dann sind die Geraden identisch und es gibt unendlich viele Lösungen! |