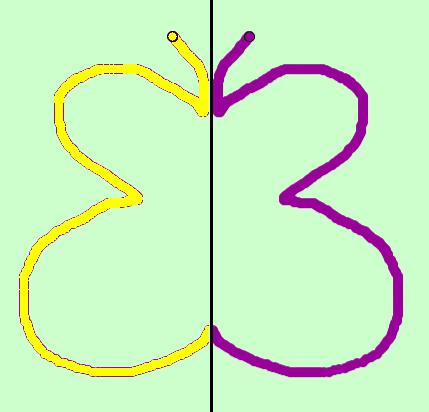Gelöschte Aufgaben: Unterschied zwischen den Versionen
| (6 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 53: | Zeile 53: | ||
<br />Kannst du die Symmetrieachse, so verschieben, dass genau '''3 Kreise''' zu sehen sind?</big><br /> | <br />Kannst du die Symmetrieachse, so verschieben, dass genau '''3 Kreise''' zu sehen sind?</big><br /> | ||
<ggb_applet height="300" width="350" showResetIcon="true" filename="Anzahl_der_Plättchen_verändern.ggb" /> | <ggb_applet height="300" width="350" showResetIcon="true" filename="Anzahl_der_Plättchen_verändern.ggb" /> | ||
| + | |||
| + | |||
| + | <big>'''Aufgabe:'''<br /> | ||
| + | Finde das passende Spiegelbild und kreuze es an! </big> | ||
| + | |||
| + | <div class="multiplechoice-quiz"> | ||
| + | [[Bild:Pferd1.jpg|120px]] (![[Bild:Pferd2.jpg|120px]]) ([[Bild:Pferda.jpg|120px]])(![[Bild:Pferd3.jpg|120px]]) | ||
| + | </div> | ||
| + | |||
| + | |||
| + | <big> '''Aufgabe:'''<br /> | ||
| + | Spiele Memory. Es passen immer zwei Bilder zusammen.</big> | ||
| + | |||
| + | <div class="memo-quiz"> | ||
| + | {| | ||
| + | |- | ||
| + | | [[Bild:Baum-Ziegler2.JPG|100px]] ||[[Bild:Baum-Ziegler.JPG|100px]] | ||
| + | |- | ||
| + | | [[Bild:Blume-Ziegler.JPG|100px]] || [[Bild:Blume-Ziegler2.JPG|100px]] | ||
| + | |- | ||
| + | | [[Bild:Haus-Ziegler.JPG|100px]] || [[Bild:Haus-Ziegler2.JPG|100px]] | ||
| + | |} | ||
| + | </div> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ---- | ||
| + | == symmetrische Figuren - zueinander symmetrische Figuren == | ||
| + | |||
| + | |||
| + | {| {{Prettytable}} | ||
| + | |- style="background-color:#66CD00" | ||
| + | ! <big> eine symmetrische Figur !! <big>zwei zueinander symmetrische Figuren | ||
| + | |- | ||
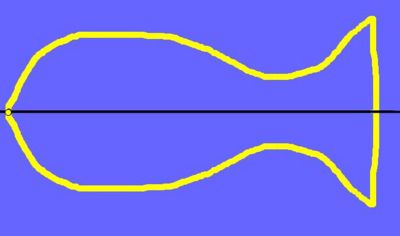
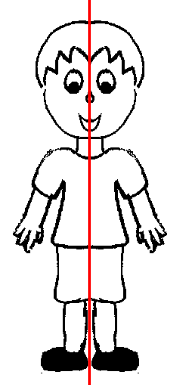
| + | |<big>Das hier ist '''eine symmetrische Figur'''. | ||
| + | [[Bild:Mann1.png]] | ||
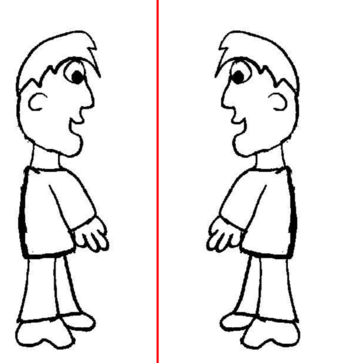
| + | ||<big> Es gibt auch Figuren die '''zueinander symmetrisch''' sind.<br /> | ||
| + | So zum Beispiel diese hier: </big><br /> | ||
| + | [[Bild:Mann.png|350px]]<br /><br /><br /> | ||
| + | |} | ||
| + | <big>Die rote Linie heißt in beiden Bildern <span style="color:#ff0000">'''Symmetrieachse'''</span>. | ||
| + | |||
| + | |||
| + | '''Aufgabe:''' | ||
| + | <br />Schaue Dir beide Bilder genau an! | ||
| + | Betrachte die Lage der Symmetrieachse. | ||
| + | <br /> | ||
| + | |||
| + | '''Lösung:''' | ||
| + | <popup><u>Im linken Bild</u> | ||
| + | liegt die '''Symmetrieachse innerhalb''' der Figur. Es entsteht '''eine symmetrische Figur'''. | ||
| + | <br /> | ||
| + | <br /> | ||
| + | <u>Im rechten Bild</u> | ||
| + | liegt die '''Symmetrieachse außerhalb'''. Beide Figuren sind '''zueinander symmetrisch'''.</popup> | ||
| + | |||
| + | = Station 7 = | ||
| + | |||
| + | <big> '''Aufgabe:'''<br /> | ||
| + | Lege das Spiegelbild!</big> | ||
| + | |||
| + | |||
| + | |||
| + | <ggb_applet height="350" width="550" showResetIcon="true" filename="Zueinander-S3.ggb" /><br /><br /><br /> | ||
Aktuelle Version vom 12. Juli 2010, 15:57 Uhr
Ergänze die folgende Figur, indem du mit dem gelben Punkt zu zeichnen beginnst.
Ergänze die folgende Figur, indem du mit dem gelben Punkt zu zeichnen beginnst.
</div>
Hier kannst du deine Vermutungen überprüfen!
| Dies ist ein besonderes Wesen. Es ist symmetrisch. Bewege die roten Punkte der linken Teilfigur und erzeuge so möglichst viele symmetrische Figuren. Was fällt dir auf? Bespreche dich mit deinem Partner! |
Aufgabe:
Kann man die Symmetrieachse, so bewegen, dass genau 5 Kreise zu sehen sind?
Aufgabe:
Kannst du die Symmetrieachse, so verschieben, dass genau 3 Kreise zu sehen sind?
Aufgabe:
Finde das passende Spiegelbild und kreuze es an!
Aufgabe:
Spiele Memory. Es passen immer zwei Bilder zusammen.
symmetrische Figuren - zueinander symmetrische Figuren
| eine symmetrische Figur | zwei zueinander symmetrische Figuren |
|---|---|
| Das hier ist eine symmetrische Figur. | Es gibt auch Figuren die zueinander symmetrisch sind. |
Die rote Linie heißt in beiden Bildern Symmetrieachse.
Aufgabe:
Schaue Dir beide Bilder genau an!
Betrachte die Lage der Symmetrieachse.
Lösung:
Station 7
Aufgabe:
Lege das Spiegelbild!