Sinus, Kosinus (Catalina Dremel, Benjamin Gallus): Unterschied zwischen den Versionen
Aus DMUW-Wiki
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 22: | Zeile 22: | ||
== Aufgabe 2 == | == Aufgabe 2 == | ||
| − | Gegeben ist die Funktion <math>f(x)= | + | Gegeben ist die Funktion <math>f(x)=a sin(x)</math>. |
<ggb_applet width="884" height="512" version="3.2" ggbBase64="UEsDBBQACAAIACy47DwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1slVXNbtswDD6vTyHotA1rYjtxkwBxi7UDhgHddsi2w26yzcRqZcnQT+v0tDfcK42Sf9J0KNadZJEU+ZEfSa8v2lqQO9CGK5nReBJRArJQJZe7jDq7PV3Si/OT9Q7UDnLNyFbpmtmMziYJ9XLHz09erU2l7gkTweQHh/uMbpkwQIlpNLDSVAD2SM5cywVnev81v4HCmoOic/JJNg6jWO1QVtTlNTfDdeoDbpW0hBj+AAg68bL1NGBZgysELzmTPl7AhkaE3PPSVhldLueUVMB3FbpL46jzViily83eWKhJ+xO0ymgyW01mq2WUzqN0Ea2iFSX7XrOIJsk8WsbRPD1bxagwBROII11MVrOzRZImabyIkjP/5FlViAt3G7AWS20Ia8EM+e40L8eC+Msnc6nEQdQoLu0Va6zTgaZZL9rYvQ+GFGqf4Hu5E9DLYqxiBcVtrtpNV7RZ5/rbvglPAp58d6WE0kRjlmmKBv2Zd2ew8UBHqyjYRMGi9+Gdjvp4lQSLcObdGawElx20PvF4yHqghLXcEC9A5767htoIloPIKCVOcnvdXX7/osTy4vaQq3/xxdU59vXjrhmdxv92+iKX6+mTdlvfgpYguqaSSK1TzpA7JgbyAo4SCl7jtVP0JWGeru8IoJOWsNMw4O6GoitY0B417hPxejqA8BgMYi0sTjfmY30ufvhspZCdS5A3rOaSfGRCOPOOXDHLkBlGPmioQVBSMutf+LESKMGZs6FfpKtB82KsHKMeDUJwPRC/SKbjZlBhyJ9U+0ALqp/pKFwHTcXwaxL3fcP2oI9KELx9VuUQuA+LpKAhJpfR09RvtZq1OIf+i+VGCWdhU2CB5bUqmA3Lr0PXL4o4irwtvpnPwlbcZ3S19B9b3sJhFrGQ/AGZZkcZHdrbVthFEozxPPfVG1pcYhMEZnDxNF2SuDDBew8hB2vSYNph0scewsbrCPHUtLhkjV/gQ2m3uMRb9Lh93b4hGWHkLa5KiRdKpn9xuXUy9Ac9vH5xCv/L7rBV0jgQ7I+R4eiFDEcvLvHjIk0fj0L4W/R/tPM/UEsHCGoxWCgYAwAAAwcAAFBLAQIUABQACAAIACy47DxqMVgoGAMAAAMHAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAUgMAAAAA" framePossible = "true" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /> | <ggb_applet width="884" height="512" version="3.2" ggbBase64="UEsDBBQACAAIACy47DwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1slVXNbtswDD6vTyHotA1rYjtxkwBxi7UDhgHddsi2w26yzcRqZcnQT+v0tDfcK42Sf9J0KNadZJEU+ZEfSa8v2lqQO9CGK5nReBJRArJQJZe7jDq7PV3Si/OT9Q7UDnLNyFbpmtmMziYJ9XLHz09erU2l7gkTweQHh/uMbpkwQIlpNLDSVAD2SM5cywVnev81v4HCmoOic/JJNg6jWO1QVtTlNTfDdeoDbpW0hBj+AAg68bL1NGBZgysELzmTPl7AhkaE3PPSVhldLueUVMB3FbpL46jzViily83eWKhJ+xO0ymgyW01mq2WUzqN0Ea2iFSX7XrOIJsk8WsbRPD1bxagwBROII11MVrOzRZImabyIkjP/5FlViAt3G7AWS20Ia8EM+e40L8eC+Msnc6nEQdQoLu0Va6zTgaZZL9rYvQ+GFGqf4Hu5E9DLYqxiBcVtrtpNV7RZ5/rbvglPAp58d6WE0kRjlmmKBv2Zd2ew8UBHqyjYRMGi9+Gdjvp4lQSLcObdGawElx20PvF4yHqghLXcEC9A5767htoIloPIKCVOcnvdXX7/osTy4vaQq3/xxdU59vXjrhmdxv92+iKX6+mTdlvfgpYguqaSSK1TzpA7JgbyAo4SCl7jtVP0JWGeru8IoJOWsNMw4O6GoitY0B417hPxejqA8BgMYi0sTjfmY30ufvhspZCdS5A3rOaSfGRCOPOOXDHLkBlGPmioQVBSMutf+LESKMGZs6FfpKtB82KsHKMeDUJwPRC/SKbjZlBhyJ9U+0ALqp/pKFwHTcXwaxL3fcP2oI9KELx9VuUQuA+LpKAhJpfR09RvtZq1OIf+i+VGCWdhU2CB5bUqmA3Lr0PXL4o4irwtvpnPwlbcZ3S19B9b3sJhFrGQ/AGZZkcZHdrbVthFEozxPPfVG1pcYhMEZnDxNF2SuDDBew8hB2vSYNph0scewsbrCPHUtLhkjV/gQ2m3uMRb9Lh93b4hGWHkLa5KiRdKpn9xuXUy9Ac9vH5xCv/L7rBV0jgQ7I+R4eiFDEcvLvHjIk0fj0L4W/R/tPM/UEsHCGoxWCgYAwAAAwcAAFBLAQIUABQACAAIACy47DxqMVgoGAMAAAMHAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAUgMAAAAA" framePossible = "true" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /> | ||
| Zeile 33: | Zeile 33: | ||
== Aufgabe 3 == | == Aufgabe 3 == | ||
| − | Verändere bei der Funktion f(x)=sin( | + | Verändere bei der Funktion <math>f(x)=sin(ax)</math> den Parameter a. |
Was passiert bei a=0? Erkläre! | Was passiert bei a=0? Erkläre! | ||
| Zeile 42: | Zeile 42: | ||
== Aufgabe 4 == | == Aufgabe 4 == | ||
| − | Wie verändert sich die Funktion wenn du den Parameter a in f(x)=sin(x+a) veränderst? | + | Wie verändert sich die Funktion wenn du den Parameter a in <math>f(x)=sin(x+a)</math> veränderst? |
Stelle zunächst eine Vermutung auf und überprüfe diese danach durch verstellen des Schiebereglers! | Stelle zunächst eine Vermutung auf und überprüfe diese danach durch verstellen des Schiebereglers! | ||
| Zeile 51: | Zeile 51: | ||
== Aufgabe 5 == | == Aufgabe 5 == | ||
| − | In der Funktion f(x)= | + | In der Funktion <math>f(x)=asin(bx+c)</math> kannst du nun alle verschiedenen Parameter verändern die eben vorgestellt wurden. |
Sag anhand deines Wissens durch die vorherigen Aufgaben voraus was bei der Veränderung des jeweiligen Parameters passiert. | Sag anhand deines Wissens durch die vorherigen Aufgaben voraus was bei der Veränderung des jeweiligen Parameters passiert. | ||
| Zeile 62: | Zeile 62: | ||
== Zusatzaufgabe == | == Zusatzaufgabe == | ||
| − | Im letzen Applet kannst du mit deinen Erkenntnissen aus Aufgabe 1 überprüfen, ob sich die Kosinus-Funktion f(x)= | + | Im letzen Applet kannst du mit deinen Erkenntnissen aus Aufgabe 1 überprüfen, ob sich die Kosinus-Funktion <math>f(x)=acos(bx+c)</math> analog zur Sinus-Funktion verhält und ob die Gemeinsamkeiten und Unterschiede weiterhin bestehen. |
<ggb_applet width="884" height="512" version="3.2" ggbBase64="UEsDBBQACAAIAHi47DwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VZLb9QwED7Dr7B8annsxrvNPqRNKygSQipwWODAzXFmE1PHXtlOm+XXM3aS3W4RokgcoCfH4/HMN/PNTLy6aGtFbsA6aXRG2SihBLQwhdRlRhu/ebmgF+dPVyWYEnLLycbYmvuMTkcTGuSNPH/6ZOUqc0u4iipfJNxmdMOVA0rc1gIvXAXgj+S8aaWS3O4+5t9AeHc46Iy809sGvXjboEzUxZV0w3YcHG6M9oQ4+R0Q9CTIVuOIZQWNULKQXAd/ERsqEXIrC19ldLE4o6QCWVZoLmVJZ00YY4v1znmoSfsVrMnoZDYdzeZsni7YfMZSSna9fD4fLZZJytJkxpbT2QRjFFwhjDQZTZd4NGdn6WLO0hne+eVRdAs3a/AeM+0Ib8EN4ZZWFvt8hM0799qog2hrpPaXfOsbG1ma9qK13wVnyKAN8b3SpYJehihFBeI6N+26y9m0M/1pt41XIp68vDTKWGLxQoohl/2ad2vUCUD3WknUSaJGbyMY3Z+z5SRqxDXv1qilpO6g9YGzIeqBEd5KR4IAjYfiGnKjeA4qo5Q0WvqrYeOluO4jZZ3+h6bOsajvlszeJPtLJlfje7W2ugarQXUVpZHYxjSO3HA1UBdxFCBkjdvuoE8ID2R9RgCdtIDSwoC764guXfH0qGrviVfjAUTA4BCr8NjaGI8PsYTO85VBbl6D/sZrqclbrlTjXpBL7jnywskbCzUoSgruw43QUwol2HA+VotuarBS7DPHaUCDEJoeSJgi4/1YMLHD72X7QAse/6KecBZsK45fI9ZXDd+BPUpBtPbeFIPj3i2SgooYXEZfpmGk1bzFLgxfPHdGNR7WAhOsr4zgPk6+Dl0/JViSBF28c3YWv3ZhWISPjWzh0ImYSPkdmeZHER2K21dYRRqcix3o7/Ya11gEkRmcOtsuSJyWEKxHT4M22WLYsc/3NYSF1xHyW2ryR03NtKdmsfwPqRH3qUkeEzWsp4ZNk3+TmxYfJi48eobcbvDh06LFzUl7SjLCyTMijDvJcW3JcyJOKRn/ROqm0XG80oOVB4fypzSzZHL0S477PdnJA8lOHpzsu+ka3/2XxLdW/x48/wFQSwcI0gZ1CzUDAABBCgAAUEsBAhQAFAAIAAgAeLjsPNIGdQs1AwAAQQoAAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAABvAwAAAAA=" framePossible = "true" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /> | <ggb_applet width="884" height="512" version="3.2" ggbBase64="UEsDBBQACAAIAHi47DwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VZLb9QwED7Dr7B8annsxrvNPqRNKygSQipwWODAzXFmE1PHXtlOm+XXM3aS3W4RokgcoCfH4/HMN/PNTLy6aGtFbsA6aXRG2SihBLQwhdRlRhu/ebmgF+dPVyWYEnLLycbYmvuMTkcTGuSNPH/6ZOUqc0u4iipfJNxmdMOVA0rc1gIvXAXgj+S8aaWS3O4+5t9AeHc46Iy809sGvXjboEzUxZV0w3YcHG6M9oQ4+R0Q9CTIVuOIZQWNULKQXAd/ERsqEXIrC19ldLE4o6QCWVZoLmVJZ00YY4v1znmoSfsVrMnoZDYdzeZsni7YfMZSSna9fD4fLZZJytJkxpbT2QRjFFwhjDQZTZd4NGdn6WLO0hne+eVRdAs3a/AeM+0Ib8EN4ZZWFvt8hM0799qog2hrpPaXfOsbG1ma9qK13wVnyKAN8b3SpYJehihFBeI6N+26y9m0M/1pt41XIp68vDTKWGLxQoohl/2ad2vUCUD3WknUSaJGbyMY3Z+z5SRqxDXv1qilpO6g9YGzIeqBEd5KR4IAjYfiGnKjeA4qo5Q0WvqrYeOluO4jZZ3+h6bOsajvlszeJPtLJlfje7W2ugarQXUVpZHYxjSO3HA1UBdxFCBkjdvuoE8ID2R9RgCdtIDSwoC764guXfH0qGrviVfjAUTA4BCr8NjaGI8PsYTO85VBbl6D/sZrqclbrlTjXpBL7jnywskbCzUoSgruw43QUwol2HA+VotuarBS7DPHaUCDEJoeSJgi4/1YMLHD72X7QAse/6KecBZsK45fI9ZXDd+BPUpBtPbeFIPj3i2SgooYXEZfpmGk1bzFLgxfPHdGNR7WAhOsr4zgPk6+Dl0/JViSBF28c3YWv3ZhWISPjWzh0ImYSPkdmeZHER2K21dYRRqcix3o7/Ya11gEkRmcOtsuSJyWEKxHT4M22WLYsc/3NYSF1xHyW2ryR03NtKdmsfwPqRH3qUkeEzWsp4ZNk3+TmxYfJi48eobcbvDh06LFzUl7SjLCyTMijDvJcW3JcyJOKRn/ROqm0XG80oOVB4fypzSzZHL0S477PdnJA8lOHpzsu+ka3/2XxLdW/x48/wFQSwcI0gZ1CzUDAABBCgAAUEsBAhQAFAAIAAgAeLjsPNIGdQs1AwAAQQoAAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAABvAwAAAAA=" framePossible = "true" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /> | ||
Aktuelle Version vom 12. Juli 2010, 22:36 Uhr
Inhaltsverzeichnis |
Sinus, Kosinus
Sowohl die Sinus- als auch die Kosinus-Funktion gehören neben dem Tangens zu den wichtigsten trigonometrischen Funktionen. Sie sin besonders wichtig bei Berechnungen am Dreieck.
Aufgabe 1
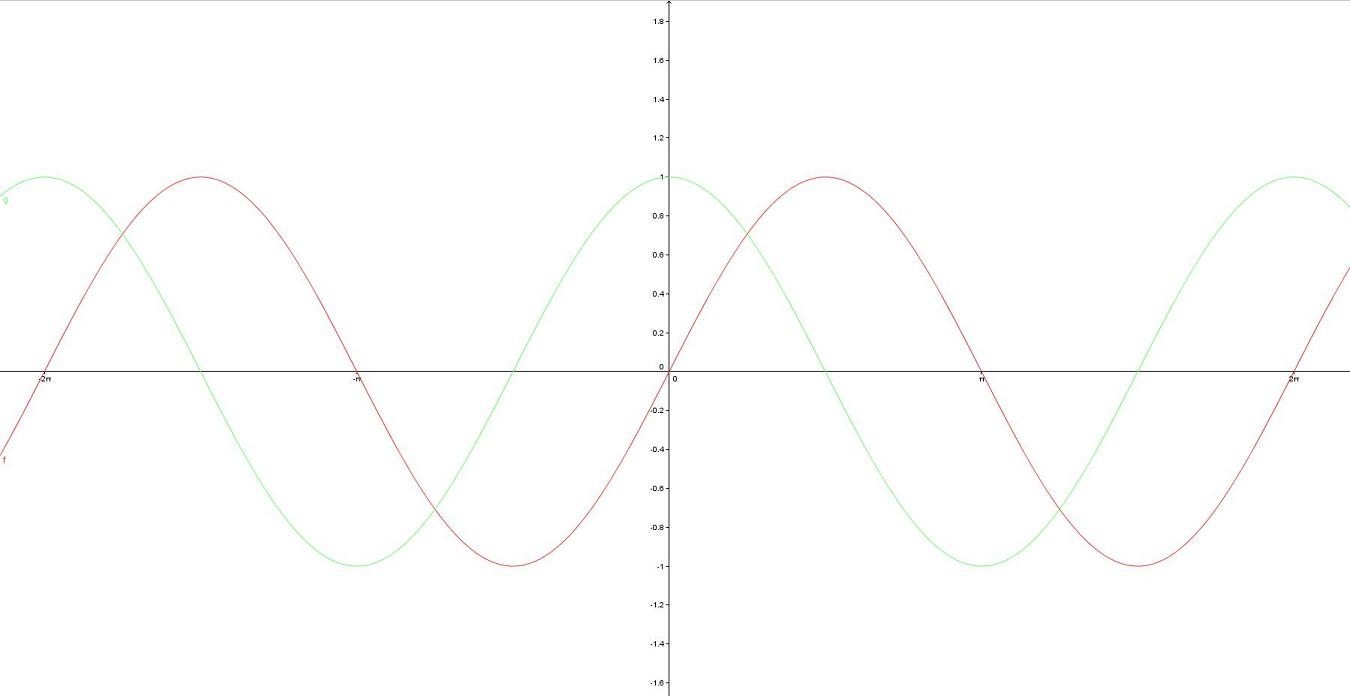
Auf dem Bild erkennst du die zwei Funktionen f und g.
Ordne den beiden Graphen die jeweilige Funktion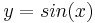 
und 
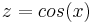zu!
Erarbeite mit deinem Nachbarn die Gemeinsamkeiten und Unterschiede der beiden Funktionen und notiere diese in deinem Heft!
Im Folgenden beschränken wir die Aufgaben auf die Sinus-Funktion. Am Ende findest du ein Applet für die Kosinus-Funktion, an der du die Beobachtungen vergleichen kannst.
Aufgabe 2
Gegeben ist die Funktion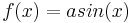 
.
Beobachte wie sich die Funktion verhält, wenn du den Parameter a veränderst!
Was passiert bei negativem a?
Aufgabe 3
Verändere bei der Funktion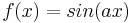 
den Parameter a.
Was passiert bei a=0? Erkläre!
Aufgabe 4
Wie verändert sich die Funktion wenn du den Parameter a in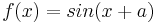 
veränderst?
Stelle zunächst eine Vermutung auf und überprüfe diese danach durch verstellen des Schiebereglers!
Aufgabe 5
In der Funktion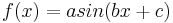 
kannst du nun alle verschiedenen Parameter verändern die eben vorgestellt wurden.
Sag anhand deines Wissens durch die vorherigen Aufgaben voraus was bei der Veränderung des jeweiligen Parameters passiert.
Stimmen diese Voraussagen überein?
Zusatzaufgabe
Im letzen Applet kannst du mit deinen Erkenntnissen aus Aufgabe 1 überprüfen, ob sich die Kosinus-Funktion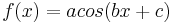 
analog zur Sinus-Funktion verhält und ob die Gemeinsamkeiten und Unterschiede weiterhin bestehen.
