Wiederholung: Unterschied zwischen den Versionen
| (84 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | = Teil 1: Wiederholung = | |
| + | <table> | ||
| + | <tr> | ||
| + | <td width="24%">[[Bild:Florianheimerl_Dimi_1wdh.png]]</td> | ||
| + | <td><div align="left">Bevor du dich mit dem Satz des Pythagoras beschäftigen kannst, musst du noch ein paar Grundlagen wiederholen.<br>In diesem Kapitel werden daher einige wichtige Grundlagen wiederholt</div></td> | ||
| + | </tr> | ||
| + | </table> | ||
| − | + | == Wiederholungen zum Dreieck == | |
| − | + | === Allgemeines zum Dreieck === | |
| − | + | <table> | |
| − | + | <tr> | |
| − | {{Aufgabe-Mathe|Beschrifte die Zeichnung.<br>Klicke dazu die Punkte | + | <td width="24%">[[Bild:Florianheimerl_Dreieck_leer.png]]</td> |
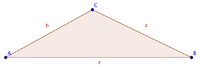
| + | <td><div align="left">Das ist ein Dreieck.<br>Ich hoffe, du kannst dich noch daran erinnern.<br>Es hat drei Seiten und drei Eckpunkte. | ||
| + | Dummerweise ist in der Zeichnung noch nichts beschriftet.<br>Aber zum Glück bist du ein alter Dreieck-Profi und kannst das für mich übernehmen. Schaue dir dazu die 1. Aufgabe an:</div></td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | <div style="font: 10pt Verdana; font-weight:bold; padding:5px; border-bottom:1px solid #AAAAAA;">Aufgabe 1</div><br> | ||
| + | {{Aufgabe-Mathe|Beschrifte die nachfolgende Zeichnung.<br>Klicke dazu die Punkte an und ziehe sie an die richtigen Stellen im Dreieck.<br>Wenn du fertig bist, dann klicke auf das Kästchen!<br> | ||
<ggb_applet height="500" width="700" showMenuBar="true" showResetIcon="true" filename="Florianheimerl_Dreieck_1.ggb" />}} | <ggb_applet height="500" width="700" showMenuBar="true" showResetIcon="true" filename="Florianheimerl_Dreieck_1.ggb" />}} | ||
| − | + | Hast du es geschafft? Super, jetzt kenne ich mich wieder etwas besser aus.<br> Hier kannst du dir die Regeln noch einmal ansehen. {{versteckt|{{Merke|Die Ecke, die der Seite a gegenüberliegt, heißt A,<br> | |
| − | die Ecke, die der Seite b gegenüberliegt heißt B,<br> | + | die Ecke, die der Seite b gegenüberliegt, heißt B,<br> |
| − | die Ecke, die der Seite c gegenüberliegt heißt C. | + | die Ecke, die der Seite c gegenüberliegt, heißt C. |
| − | + | }}}} | |
| − | <div class="schuettel-quiz"> | + | <table> |
| − | + | <tr> | |
| − | + | <td width="24%">[[Bild:Florianheimerl_Dimi_frage.png]]</td> | |
| − | </div> | + | <td><div style="font: 10pt Verdana; font-weight:bold; padding:5px; border-bottom:1px solid #AAAAAA;">Aufgabe 2</div><br><div align="left"><div class="schuettel-quiz"> |
| − | + | Diese Darstellung ist schon gut. Es fehlt aber noch etwas.<br>Fülle die Lücke aus und drücke auf prüfen.<br>Ein Dreieck hat doch auch noch drei '''Winkel'''?<br>Ein komisches Wort, oder? Aber ihre Bezeichnungen sind noch komischer: α, β und γ. | |
| − | <div class="lueckentext-quiz">{{Aufgabe-Mathe|Ordne die Winkel den richtigen Seiten zu | + | <br></div> |
| + | <quiz display="simple"> | ||
| + | {Weißt du, aus welcher Sprache die Bezeichnungen α, β und γ stammen?} | ||
| + | - Deutsch | ||
| + | + Griechisch | ||
| + | - Spanisch | ||
| + | </quiz></div></td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | <br>Ich weiß leider nicht mehr genau, wie sie angeordnet sind.<br>Aber zum Glück kannst du mir dabei ja helfen. | ||
| + | <div style="font: 10pt Verdana; font-weight:bold; padding:5px; border-bottom:1px solid #AAAAAA;">Aufgabe 3</div><br> | ||
| + | <div class="lueckentext-quiz">{{Aufgabe-Mathe|Ordne die Winkel den richtigen Seiten zu, indem du sie mit gedrückter linker Maustaste verschiebst. Klicke danach auf "Prüfen".<br> | ||
Der Winkel an der Ecke A heißt <strong>α</strong> und wird gebildet von den Seiten <strong>b und c</strong>.<br> | Der Winkel an der Ecke A heißt <strong>α</strong> und wird gebildet von den Seiten <strong>b und c</strong>.<br> | ||
Der Winkel an der Ecke B heißt <strong>β</strong> und wird gebildet von den Seiten <strong>a und c</strong>.<br> | Der Winkel an der Ecke B heißt <strong>β</strong> und wird gebildet von den Seiten <strong>a und c</strong>.<br> | ||
| Zeile 25: | Zeile 48: | ||
}}</div> | }}</div> | ||
<br> | <br> | ||
| − | + | Wunderbar!<br>Jetzt haben wir ja schon einiges zum Thema Dreieck wiederholt.<br>Ich habe dir noch einmal alles übersichtlich zusammengefasst: {{versteckt|{{Merke|[[Bild:Florianheimerl_Dreieck_fertig.png]] | |
| − | + | }}}} | |
<br> | <br> | ||
| − | + | Schauen wir doch einmal, was du sonst noch so über Dreiecke weißt.<br> | |
| − | + | ||
| − | + | ||
| − | + | ||
| + | <div style="font: 10pt Verdana; font-weight:bold; padding:5px; border-bottom:1px solid #AAAAAA;">Aufgabe 4</div><br> | ||
| + | {{Aufgabe-Mathe|Versuche herauszufinden, welches Dreieck zu welcher Beschreibung passt.<br>Ordne die Beschreibungen den Dreiecken zu, indem du sie mit gedrückter linker Maustaste verschiebst.<br>Wenn du fertig bist, drücke auf "Prüfen"<br>}} | ||
| + | <div class="zuordnungs-quiz"> | ||
{| | {| | ||
| − | | gleichschenkliges Dreieck || zwei Seiten sind gleich lang | + | | [[Bild:Florianheimerl_Gleichschenklig.png]] || gleichschenkliges Dreieck || zwei Seiten sind gleich lang |
|- | |- | ||
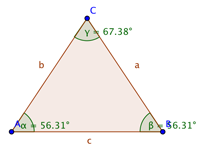
| − | | spitzwinkliges Dreieck || alle drei Winkel < 90° | + | | [[Bild:Florianheimerl_Spitzwinklig.png]] || spitzwinkliges Dreieck || alle drei Winkel < 90° |
|- | |- | ||
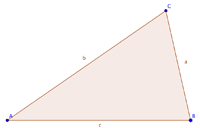
| − | | stumpfwinkliges Dreieck || ein Winkel > 90° | + | | [[Bild:Florianheimerl_Stumpfwinklig.png]] || stumpfwinkliges Dreieck || ein Winkel > 90° |
|- | |- | ||
| − | | gleichseitiges Dreieck || alle drei Seiten sind gleich lang || alle drei Winkel sind gleich groß (60°) | + | | [[Bild:Florianheimerl_Gleichseitig.png]] || gleichseitiges Dreieck || alle drei Seiten sind gleich lang || alle drei Winkel sind gleich groß (60°) |
|- | |- | ||
| − | | rechtwinkliges Dreieck || ein Winkel beträgt genau 90° | + | | [[Bild:Florianheimerl_Rechtwinklig.png]] || rechtwinkliges Dreieck || ein Winkel beträgt genau 90° |
|} | |} | ||
| − | |||
</div> | </div> | ||
<br> | <br> | ||
| − | + | Du bist dir noch ein wenig unsicher? Kein Problem - Ich habe dir alle Regeln noch einmal übersichtlich zusammengefasst. {{versteckt|{{Merke|gleichschenkliges Dreieck: zwei Seiten(zwei Schenkel) sind gleich lang<br> | |
spitzwinkliges Dreieck: alle drei Winkel <(kleiner als) 90°<br> | spitzwinkliges Dreieck: alle drei Winkel <(kleiner als) 90°<br> | ||
stumpfwinkliges Dreieck: ein Winkel >(größer als) 90°<br> | stumpfwinkliges Dreieck: ein Winkel >(größer als) 90°<br> | ||
gleichseitiges Dreieck: alle drei Seitensind gleich lang; alle drei Winkel sind gleich groß (60°)<br> | gleichseitiges Dreieck: alle drei Seitensind gleich lang; alle drei Winkel sind gleich groß (60°)<br> | ||
rechtwinkliges Dreieck: ein Winkel beträgt genau 90° | rechtwinkliges Dreieck: ein Winkel beträgt genau 90° | ||
| − | }}}}}} | + | }}}} |
| + | |||
| + | <br> | ||
| + | Da du ja nun wieder ein echter Dreieck-Experte zu sein scheinst, können wir uns nun mit meinem Lieblingsdreieck beschäftigen, dem rechtwinkligen Dreieck.<br>Wollen wir doch mal sehen, was du dazu noch weißt.<br><br> | ||
| + | |||
| + | === Das rechtwinklige Dreieck === | ||
| + | <br><div style="font: 10pt Verdana; font-weight:bold; padding:5px; border-bottom:1px solid #AAAAAA;">Aufgabe 5</div><br> | ||
| + | {{Aufgabe-Mathe|Verschiebe den Punkt C so, dass ein rechtwinkliges Dreieck entsteht.<br>Klicke anschließend auf das Kästchen.<br> | ||
| + | <ggb_applet height="500" width="700" showMenuBar="true" showResetIcon="true" filename="Florianheimerl_Dreieckrw.ggb" />}}<br> | ||
| + | |||
| + | Super!<br>Um genau dieses Dreieck geht es im Satz des Pythagoras.<br>Die Seiten des rechtwinkligen Dreiecks haben besondere Bezeichnungen.<br> | ||
| + | {{Merke|In einem rechtwinkligen Dreieck heißt die längste Seite immer Hypotenuse und die anderen beiden Seiten Katheten.<br> | ||
| + | Die Hypotenuse liegt immer dem 90°-Winkel gegenüber.<br> | ||
| + | Die beiden Katheten schließen immer den 90°-Winkel ein. | ||
| + | }} | ||
| + | |||
| + | Du kannst dir das noch nicht richtig vorstellen? Kein Problem!<br> | ||
| + | So sieht das dann aus:<br> | ||
| + | |||
| + | <table> | ||
| + | <tr> | ||
| + | <td width="24%">[[Bild:Florianheimerl_Dreieck_pyth.png]]</td> | ||
| + | <td><div align="left">[[Bild:Florianheimerl_Dimi_achtung.png]]</div></td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | |||
| + | <br> | ||
| + | Super! - Jetzt haben wir das Wichtigste zum Dreieck wiederholt.<br> | ||
| + | Jetzt schauen wir uns noch gemeinsam Wurzeln an.<br> | ||
| + | |||
| + | == Potenzen und Wurzeln == | ||
| + | === Die Potenz === | ||
| + | |||
| + | |||
| + | Du kannst dich sicherlich noch an die Potenzschreibweise erinnern. Ich habe dir noch einmal ein Beispiel mitgebracht.<br> | ||
| + | c² = 4<br> | ||
| + | In dieser Aufgabe möchte wann herausfinden: Welche Zahl quadriert ergibt 4?<br> | ||
| + | Oder einfacher ausgedrückt: Welche Zahl muss ich „hoch 2“ nehmen, dass ich die Zahl 4 erhalte?<br> | ||
| + | <div style="font: 10pt Verdana; font-weight:bold; padding:5px; border-bottom:1px solid #AAAAAA;">Aufgabe 6</div><br> | ||
| + | <quiz display="simple"> | ||
| + | {Um das herauszufinden müssen wir aber wissen, was c² bedeutet. Kannst du mir dabei helfen?} | ||
| + | - c² = c + c | ||
| + | - c² = c : c | ||
| + | + c² = c ˑ c | ||
| + | </quiz> | ||
| + | |||
| + | Genau!<br>Daraus lernen wir also:<br> | ||
| + | {{Merke|Wenn ich eine Zahl quadriere („hoch 2“ nehme), dann ist das das Gleiche, wie wenn ich die Zahl mit sich selber multipliziere.}}<br><br> | ||
| + | Schaue dir dazu noch ein paar weitere Beispiele an:<br> | ||
| + | a = 4 → a² = a ˑ a = 4 ˑ 4 = 16<br> | ||
| + | x = 7 → x² = x ˑ x = 7 ˑ 7 = 49<br><br> | ||
| + | Genauso funktioniert das auch, wenn man zusätzliche Maßeinheiten dazu nimmt:<br> | ||
| + | a = 4 cm → a² = a ˑ a = 4 cm ˑ 4 cm = 16 cm²<br> | ||
| + | x = 7 cm → x² = x ˑ x = 7 cm ˑ 7 cm = 49 cm²<br><br> | ||
| + | Um hier auf die richtige Lösung zu kommen haben wir die Zahlen miteinander multipliziert ( 4 ˑ 4 = 16 oder 7 ˑ 7 = 49 ) und die Maßeinheiten miteinander multipliziert ( cm ˑ cm = cm² ).<br><br> | ||
| + | |||
| + | <table border="0" style="margin-bottom: 0.4em; margin-left: auto; margin-right: auto; width: 100%; background-color: #efefef"> | ||
| + | <tr> | ||
| + | <td width="24%">[[Bild:Florianheimerl_Dimi_achtung.png]]</td> | ||
| + | <td><div align="left"><b>Achtung:</b><br>Du kannst nur Zahlenwerte miteinander multiplizieren, die auch die gleiche Maßeinheit haben.</div></td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | |||
| + | Das, was wir hier nun wiederholen möchten, ist die Umkehrung des Quadrierens.<br> | ||
| + | Wie komme ich also vom Quadrat einer Zahl auf die Ausgangszahl? <br> | ||
| + | |||
| + | === Die Wurzel === | ||
| + | |||
| + | <table border="0" style="margin-bottom: 0.4em; margin-left: auto; margin-right: auto; width: 100%; background-color: #efefef"> | ||
| + | <tr> | ||
| + | <td width="50%"><div align="left">Beispiel: <b>c² = 4</b><br> | ||
| + | Wie kann ich berechnen, was c ist?<br><br> | ||
| + | Dazu erinnern wir uns an das Quadrieren.<br> | ||
| + | c² = 4 → c² = c ˑ c = 4<br><br> | ||
| + | <b>Das bedeutet: Wir suchen eine Zahl, die, wenn man sie mit sich selbst multipliziert, 4 ergibt.</b><br><br> | ||
| + | Das ist leicht zu erraten, oder?<br> | ||
| + | c² = c ˑ c = 2 ˑ 2 = 4<br> | ||
| + | 2 ˑ 2 = 4<br> | ||
| + | Die Zahl ist also 2.<br><br> | ||
| + | <b>Man kann also sagen:</b><br> | ||
| + | 2² ergibt 4! (2² = 4 )<br><br> | ||
| + | Wenn ich die Zahl 2 quadriere, erhalte ich die Zahl 4.</div></td> | ||
| + | <td><div align="left"></div></td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | |||
| + | <br><br> | ||
| + | Die gesuchte Zahl ist jedoch nicht immer so leicht zu erraten.<br><br> | ||
| + | Mit dem Taschenrechner können wir die gesuchten Zahlen aber sehr einfach berechnen!<br><br> | ||
| + | |||
| + | {{Merke|Du hast auf deinem Taschenrechner folgendes Symbol:<br>[[Bild:Florianheimerl_Wurzel.gif]] | ||
| + | Das ist die Wurzeltaste!}}<br> | ||
| + | |||
| + | <table border="0" style="margin-bottom: 0.4em; margin-left: auto; margin-right: auto; width: 100%; background-color: #efefef"> | ||
| + | <tr> | ||
| + | <td width="30%"><div align="center"><b>Das Wurzelziehen ist die Umkehrung des Quadrierens.<br><br>c² = 4<br>→ c ist die Wurzel aus 4</b><br><br></div></td> | ||
| + | <td><div align="left">[[Bild:Florianheimerl_Dimi_achtung.png]]</div></td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | |||
| + | <div style="font: 10pt Verdana; font-weight:bold; padding:5px; border-bottom:1px solid #AAAAAA;">Aufgabe 7</div><br> | ||
| + | <quiz display="simple"> | ||
| + | {Welcher Rechenweg würde in der nächsten Aufgabe zum Ziel führen?} | ||
| + | + x² = 25<br>x² = x ˑ x = 5 ˑ 5 = 25 → x = 5<br> | ||
| + | - e² = 16<br>e² = e ˑ e = 8 + 8 = 16 → e = 8<br> | ||
| + | - y² = 7<br>y² = 7 ˑ 1 = 7 → y = 7<br> | ||
| + | </quiz> | ||
| + | <br> | ||
| + | |||
| + | == Zusammenfassung == | ||
| + | |||
| + | {{Merke|Die Ecke, die der Seite a gegenüberliegt heißt A,<br> | ||
| + | die Ecke, die der Seite b gegenüberliegt heißt B,<br> | ||
| + | die Ecke, die der Seite c gegenüberliegt heißt C.<br><br> | ||
| + | [[Bild:Florianheimerl_Dreieck_fertig.png]]<br> | ||
| + | gleichschenkliges Dreieck: zwei Seiten(zwei Schenkel) sind gleich lang<br> | ||
| + | spitzwinkliges Dreieck: alle drei Winkel <(kleiner als) 90°<br> | ||
| + | stumpfwinkliges Dreieck: ein Winkel >(größer als) 90°<br> | ||
| + | gleichseitiges Dreieck: alle drei Seiten sind gleich lang; alle drei Winkel sind gleich groß (60°)<br> | ||
| + | rechtwinkliges Dreieck: ein Winkel beträgt genau 90°<br><br> | ||
| + | <b>In einem rechtwinkligen Dreieck heißt die längste Seite immer Hypotenuse und die anderen beiden Seiten Katheten.</b><br> | ||
| + | Die Hypotenuse liegt immer gegenüber des 90°-Winkels. Die beiden Katheten schließen immer den 90°-Winkel ein.<br><br> | ||
| + | <b>Wenn ich eine Zahl quadriere („hoch 2“ nehme), dann ist das das Gleiche, wie wenn ich die Zahl mit sich selbst multipliziere.</b><br> | ||
| + | Du hast auf deinem Taschenrechner folgendes Symbol:<br>[[Bild:Florianheimerl_Wurzel.gif]] | ||
| + | Das ist die Wurzeltaste!<br> | ||
| + | Das Wurzelziehen ist die Umkehrung des Quadrierens.<br> | ||
| + | }} | ||
| + | c² = 4<br>→ c ist die Wurzel aus 4 | ||
| + | |||
| + | |||
<br> | <br> | ||
| + | <br>Du bist nun soweit - Lass uns mit dem Satz des Pythagoras weitermachen! | ||
| − | |||
| − | |||
| − | |||
| − | [[Bild:Florianheimerl_Dimi_2sdp.png]][[Lernpfade/Satz des Pythagoras/Satz des Pythagoras|Weiter zu | + | [[Bild:Florianheimerl_Dimi_2sdp.png]][[Lernpfade/Satz des Pythagoras/Satz des Pythagoras|Weiter zu Teil 2: Satz des Pythagoras]] |
| + | [[Bild:Florianheimerl_Dimi.png]][[Lernpfade/Satz des Pythagoras|zurück zur Übersicht]] | ||
Aktuelle Version vom 21. September 2010, 05:19 Uhr
Inhaltsverzeichnis |
Teil 1: Wiederholung
 |
Bevor du dich mit dem Satz des Pythagoras beschäftigen kannst, musst du noch ein paar Grundlagen wiederholen. In diesem Kapitel werden daher einige wichtige Grundlagen wiederholt |
Wiederholungen zum Dreieck
Allgemeines zum Dreieck
|
Beschrifte die nachfolgende Zeichnung. |
Hast du es geschafft? Super, jetzt kenne ich mich wieder etwas besser aus.
Hier kannst du dir die Regeln noch einmal ansehen.
30px Merke
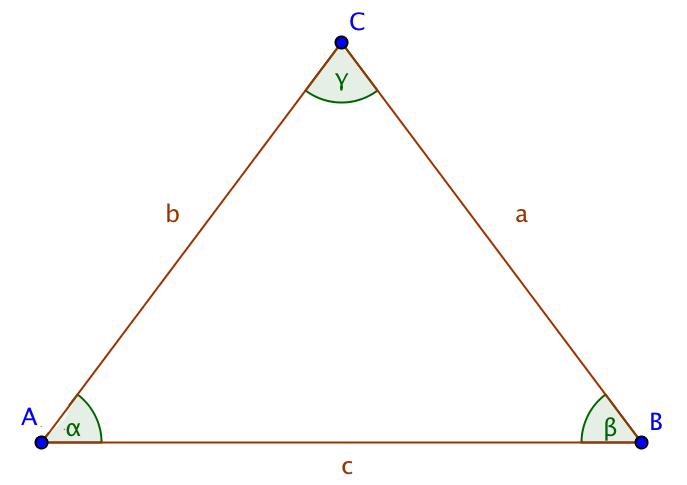
Die Ecke, die der Seite a gegenüberliegt, heißt A, |
Ich weiß leider nicht mehr genau, wie sie angeordnet sind.
Aber zum Glück kannst du mir dabei ja helfen.
|
Ordne die Winkel den richtigen Seiten zu, indem du sie mit gedrückter linker Maustaste verschiebst. Klicke danach auf "Prüfen". |
Wunderbar!
Jetzt haben wir ja schon einiges zum Thema Dreieck wiederholt.
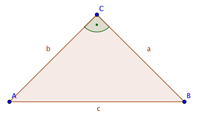
Ich habe dir noch einmal alles übersichtlich zusammengefasst:
30px Merke
|
Schauen wir doch einmal, was du sonst noch so über Dreiecke weißt.
|
Versuche herauszufinden, welches Dreieck zu welcher Beschreibung passt. |
Du bist dir noch ein wenig unsicher? Kein Problem - Ich habe dir alle Regeln noch einmal übersichtlich zusammengefasst.
30px Merke
gleichschenkliges Dreieck: zwei Seiten(zwei Schenkel) sind gleich lang |
Da du ja nun wieder ein echter Dreieck-Experte zu sein scheinst, können wir uns nun mit meinem Lieblingsdreieck beschäftigen, dem rechtwinkligen Dreieck.
Wollen wir doch mal sehen, was du dazu noch weißt.
Das rechtwinklige Dreieck
|
Verschiebe den Punkt C so, dass ein rechtwinkliges Dreieck entsteht. |
Super!
Um genau dieses Dreieck geht es im Satz des Pythagoras.
Die Seiten des rechtwinkligen Dreiecks haben besondere Bezeichnungen.
30px Merke
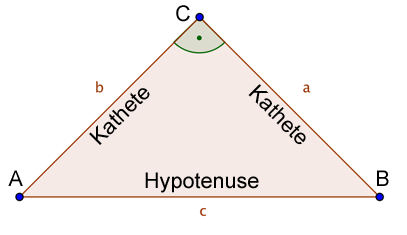
In einem rechtwinkligen Dreieck heißt die längste Seite immer Hypotenuse und die anderen beiden Seiten Katheten. |
Du kannst dir das noch nicht richtig vorstellen? Kein Problem!
So sieht das dann aus:
 |
Super! - Jetzt haben wir das Wichtigste zum Dreieck wiederholt.
Jetzt schauen wir uns noch gemeinsam Wurzeln an.
Potenzen und Wurzeln
Die Potenz
Du kannst dich sicherlich noch an die Potenzschreibweise erinnern. Ich habe dir noch einmal ein Beispiel mitgebracht.
c² = 4
In dieser Aufgabe möchte wann herausfinden: Welche Zahl quadriert ergibt 4?
Oder einfacher ausgedrückt: Welche Zahl muss ich „hoch 2“ nehmen, dass ich die Zahl 4 erhalte?
Genau!
Daraus lernen wir also:
30px Merke
Wenn ich eine Zahl quadriere („hoch 2“ nehme), dann ist das das Gleiche, wie wenn ich die Zahl mit sich selber multipliziere. |
Schaue dir dazu noch ein paar weitere Beispiele an:
a = 4 → a² = a ˑ a = 4 ˑ 4 = 16
x = 7 → x² = x ˑ x = 7 ˑ 7 = 49
Genauso funktioniert das auch, wenn man zusätzliche Maßeinheiten dazu nimmt:
a = 4 cm → a² = a ˑ a = 4 cm ˑ 4 cm = 16 cm²
x = 7 cm → x² = x ˑ x = 7 cm ˑ 7 cm = 49 cm²
Um hier auf die richtige Lösung zu kommen haben wir die Zahlen miteinander multipliziert ( 4 ˑ 4 = 16 oder 7 ˑ 7 = 49 ) und die Maßeinheiten miteinander multipliziert ( cm ˑ cm = cm² ).
 |
Achtung: Du kannst nur Zahlenwerte miteinander multiplizieren, die auch die gleiche Maßeinheit haben. |
Das, was wir hier nun wiederholen möchten, ist die Umkehrung des Quadrierens.
Wie komme ich also vom Quadrat einer Zahl auf die Ausgangszahl?
Die Wurzel
Beispiel: c² = 4 Wie kann ich berechnen, was c ist? |
Die gesuchte Zahl ist jedoch nicht immer so leicht zu erraten.
Mit dem Taschenrechner können wir die gesuchten Zahlen aber sehr einfach berechnen!
30px Merke
Du hast auf deinem Taschenrechner folgendes Symbol: |
Das Wurzelziehen ist die Umkehrung des Quadrierens. c² = 4 → c ist die Wurzel aus 4 |
Zusammenfassung
30px Merke
Die Ecke, die der Seite a gegenüberliegt heißt A, |
c² = 4
→ c ist die Wurzel aus 4
Du bist nun soweit - Lass uns mit dem Satz des Pythagoras weitermachen!