Flächeninhalt Parallelogramm: Unterschied zwischen den Versionen
K (→Einstieg) |
K (→Dem Flächeninhalt auf der Spur) |
||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 65: | Zeile 65: | ||
*'''Nebenwinkel''' im Parallelogramm ergänzen sich zu 180° | *'''Nebenwinkel''' im Parallelogramm ergänzen sich zu 180° | ||
*Die Innenwinkelsumme im Dreieck beträgt '''180°''' | *Die Innenwinkelsumme im Dreieck beträgt '''180°''' | ||
| − | *Nebenwinkel: '''<math>\alpha + \beta = </math> 180°''' | + | |
| − | *Gegenüberliegende Winkel im Parallelogramm:'''<math>\alpha = \alpha_1 </math>''' | + | <br> |
| + | *damit sind Nebenwinkel im Parallelogramm: '''<math>\alpha + \beta = </math> 180°''' | ||
| + | <br> | ||
| + | *Gegenüberliegende Winkel im Parallelogramm sind : | ||
| + | <br> | ||
| + | '''<math>\alpha = \alpha_1 </math>''' <br> und | ||
<math>\beta = \gamma + </math> '''90°''' bzw. | <math>\beta = \gamma + </math> '''90°''' bzw. | ||
<math>\beta = \gamma + \epsilon</math> | <math>\beta = \gamma + \epsilon</math> | ||
| + | <br> | ||
| + | <br> | ||
*'''Innenwinkelsumme im Dreieck''': <math>\alpha + \beta + \epsilon = </math> 180° | *'''Innenwinkelsumme im Dreieck''': <math>\alpha + \beta + \epsilon = </math> 180° | ||
<br> | <br> | ||
Aktuelle Version vom 3. August 2009, 10:04 Uhr
Flächeninhalt Parallelogramm
Einstieg
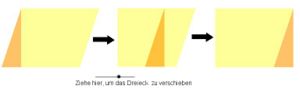
- Lass uns hier gemeinsam die Formel für den Flächeninhalt des Parallelogramms erarbeiten. Du wirst sehen, es ist gar nicht so schwer!
|
Ziehe am roten und grünen Eckpunkt des Vierecks.
Die andere Seite ist 5(Zahl eintragen)cm lang. b. Erzeuge ein Quadrat mit Umfang 12 cm. Welchen Flächeninhalt hat es? Es hat einen Flächeninhalt von 9(Zahl eintragen)cm². c. Erzeuge ein Parallelogramm mit 2 rechten Winkeln und dem Flächeninhalt 8cm². Eine Seite beträgt 2cm. Wie groß ist die andere Seite? Die andere Seite ist 4(Zahl eintragen) cm lang.
|
Dem Flächeninhalt auf der Spur
|
Denke an die Innenwinkelsumme im Dreieck und Paralellogramm! Lasse Dir dazu die Winkel anzeigen.
| |
| 3. Verändert sich Größe Gesamtfläche?
Der Flächeninhalt des Rechtecks beträgt 12 (Zahl eintragen)cm²
|
Wie war das doch?
Maja hat sich nicht alles gemerkt.
Nils hat ihr die Herleitungsidee nochmals zusammengefasst:

Maja: "Ah, ich habe es jetzt verstanden! Ich zerlege das Parallelogramm und ergänze zum Rechteck. Von Rechtecken kann ich den Flächeninhalt einfach über Länge mal Breite berechnen.
Die Länge des Rechtecks entspricht dabei der Grundseite des Parallelogramms. Doch wie war das mit der Breite im Parallelogramm??"
Nils: "Die Breite im Parallelogramm nennt man eigentlich Höhe, doch das zeige ich Dir auf der folgenden Seite"
Hier geht es weiter zum nächsten Abschnitt:
→Höhen im Parallelogramm

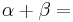 180°
180°
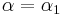
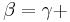 90° bzw.
90° bzw.
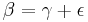
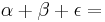 180°
180°

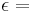 90° und
90° und 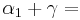 90°
90°