Variation am Dreieck: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
K (→‎Variation am Dreieck)
(→‎Flächeninhalt von stumpfwinkligen Dreiecken: Frage zu stumpfwinkligem Dreieck eingeführt)
 
(4 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 4: Zeile 4:
 
<div style="border: 2px solid white; background-color:#ffffff; padding:7px;">
 
<div style="border: 2px solid white; background-color:#ffffff; padding:7px;">
 
{|  
 
{|  
−
'''''Du siehst hier ein Dreieck, bei dem die Seiten gegeben sind:'''''<br>
+
 
−
<span style="color: blue"><math>a = 3 cm</math></span>, <span style="color: purple"><math>b = 4 cm</math></span> <br> und <math>c =5 cm </math>
+
 
|<ggb_applet height="400" width="700" showResetIcon="true" filename="Ebert_rechtwinkligesDreieck.ggb" />||
 
|<ggb_applet height="400" width="700" showResetIcon="true" filename="Ebert_rechtwinkligesDreieck.ggb" />||
−
*'''''Maja will den Flächeninhalt des Dreiecks ABC berechnen.'''''
+
'''''Gegeben sind die  Seiten:'''''<br>
−
*'''''Welches spezielle Dreieck ist das Dreieck ABC?''''' <br>
+
'''<span style="color: blue">a =3cm</span>, <span style="color: purple">b= 4cm</span> und c = 5cm '''
−
'''''Schaffst Du es auch ohne den zweiten Hinweis?'''''<br>
+
−
{{ versteckt| Dreieck ABC ist ein rechtwinkliges Dreieck }}
+
  
−
*'''''Ist nicht schon eine Höhe gegeben, die Maja verwenden kann?'''''
+
*<span style="color: green">'''''Zeig Maja´s Überlegung an'''''</span>
−
*'''''Zeig den Hinweis von Nils im Applet an'''''<br> <br>
+
  
−
{{ versteckt| Die Seiten a und b des Dreiecks ABC können jeweils als Grundseite und als dazugehörige Höhe verwendet werden, da das Dreieck ABC rechtwinklig ist und a senkrecht zu b ist.}}
 
  
−
*'''''Berechne den Flächeninhalt des Dreiecks'''''  
+
*'''''Ist nicht schon eine Höhe gegeben? Zeig den <span style="color: red">Hinweis von Nils</span> an'''''  
 +
'<br>
 +
*'''''Welches spezielle Dreieck ist das Dreieck ABC?''''' <br>
 +
'''''Brauchst Du den  Hinweis?'''''<br>
 +
{{ versteckt| Dreieck ABC ist rechtwinklig }}
 +
* '''''Maja hat eine Lösung gefunden''''' [[Bild:Ebert_MotivatorGrün.jpg|50px|right]]
 +
{{ versteckt| '''Die <u>Seiten a und b</u> des Dreiecks ABC sind <u>gleichzeitig auch Grundseite und  Höhe</u>, da das Dreieck ABC rechtwinklig ist und somit a senkrecht zu b ist.'''}}
  
 
<div class="lueckentext-quiz">  
 
<div class="lueckentext-quiz">  
−
Es gilt zum Beispiel:
+
*Es gilt zum Beispiel:<br>
−
Länge Grundseite b: '''4 (cm)'''<br>
+
Seite b ist Grundseite, damit ist die Länge der Grundseite b '''4 (cm)'''<br>
−
Länge der zugehörigen Höhe a : 3 cm <br>
+
*Die Seite a wird damit zur Höhe und da: a = 3 cm <br>
−
Der Flächeninhalt des Dreiecks beträgt '''6(cm²)'''
+
ist der Flächeninhalt des Dreiecks '''6(cm²)'''
 
</div>
 
</div>
 
|}
 
|}
Zeile 36: Zeile 37:
 
<div style="border: 2px solid red; background-color:#ffffff; padding:7px;">
 
<div style="border: 2px solid red; background-color:#ffffff; padding:7px;">
 
{|  
 
{|  
−
|[[Bild:Ebert_MotivatorMerke.jpg|100px]]|| '''Der Flächeninhalt eines rechtwinkligen Dreiecks berechnet sich durch''' :  
+
|[[Bild:Ebert_MotivatorMerke.jpg|100px]]|| '''Der Flächeninhalt eines <u>rechtwinkligen Dreiecks</u> berechnet sich durch''' :  
 
:::::::::F<sub>rechtwinklig</sub> = '''<math>{1 \over 2}</math>''' <math>\cdot</math>  <span style="color: purple">'''b'''</span> <math>\cdot</math> <span style="color: blue">'''a'''</span>
 
:::::::::F<sub>rechtwinklig</sub> = '''<math>{1 \over 2}</math>''' <math>\cdot</math>  <span style="color: purple">'''b'''</span> <math>\cdot</math> <span style="color: blue">'''a'''</span>
  
−
'''wobei <span style="color: blue">'''a'''</span> und <span style="color: green">'''b'''</span> senkrecht zu einander stehen.'''  
+
'''wobei die Seiten <span style="color: blue">a</span> und <span style="color: purple">b</span> senkrecht zueinander stehen.'''  
 
<br>
 
<br>
 
|}
 
|}
Zeile 54: Zeile 55:
 
====Wie lautet die Flächeninhaltsformel für ein====
 
====Wie lautet die Flächeninhaltsformel für ein====
  
−
:'''..gleichschenklig-rechtwinkliges Dreieck ABC ?'''
+
:'''..gleichschenklig-rechtwinkliges Dreieck EFD ?'''
 
:'''Der rechte Winkel befindet sich am Eckpunkt D.'''''  
 
:'''Der rechte Winkel befindet sich am Eckpunkt D.'''''  
 
[[Bild:Ebert_gleichschenklig.jpg|center]]
 
[[Bild:Ebert_gleichschenklig.jpg|center]]
−
<div style="border: 2px solid blue; background-color:#ffffff; padding:7px;">
+
<div style="border: 2px solid green; background-color:#ffffff; padding:7px;">
 
{|  
 
{|  
 
'''''Ergänze die fehlenden Felder und ermittle daraus die Flächeninhaltsformel für das gleichschenklig-rechtwinklige Dreieck:'''''
 
'''''Ergänze die fehlenden Felder und ermittle daraus die Flächeninhaltsformel für das gleichschenklig-rechtwinklige Dreieck:'''''
Zeile 64: Zeile 65:
 
:::F<sub>rechtwinklig</sub> = '''<math>{1 \over 2}</math>''' <math>\cdot</math>  '''e''' <math>\cdot</math> f
 
:::F<sub>rechtwinklig</sub> = '''<math>{1 \over 2}</math>''' <math>\cdot</math>  '''e''' <math>\cdot</math> f
 
2. Im gleichschenkligen Dreieck gilt für die Seiten f und e:<br>
 
2. Im gleichschenkligen Dreieck gilt für die Seiten f und e:<br>
−
::::f = e
+
::::f '''=''' e
  
−
<math>\Rightarrow</math> Für den Flächeninhalt F eines rechtwinkligen und gleichschenkligen Dreiecks gilt:<br>
+
<math>\Rightarrow</math> Für den Flächeninhalt F eines rechtwinkligen und gleichschenkligen Dreiecks gilt also zum Beispiel:<br>
 
F = <math>{1 \over 2}</math> <math>\cdot</math>  '''e''' <math>\cdot</math> e = <math>{1 \over 2}</math> <math>\cdot</math>'''e²'''
 
F = <math>{1 \over 2}</math> <math>\cdot</math>  '''e''' <math>\cdot</math> e = <math>{1 \over 2}</math> <math>\cdot</math>'''e²'''
 
</div>
 
</div>
Zeile 89: Zeile 90:
 
{|  
 
{|  
 
|<ggb_applet height="400" width="700" showResetIcon="true" filename="Ebert_DreieckScherung.ggb" />||
 
|<ggb_applet height="400" width="700" showResetIcon="true" filename="Ebert_DreieckScherung.ggb" />||
−
*'''''Ziehe den <span style="color: red">roten Eckpunkt C</span> zu auf die Punkte <span style="color: orange">D</span>, <span style="color: pink">E</span> und <span style="color: green">F</span>.'''''
+
*'''''Ziehe den <span style="color: red">roten Eckpunkt C</span> auf die Punkte <span style="color: orange">D</span>, <span style="color: pink">E</span> und <span style="color: green">F</span>.'''''
  
 
<quiz display="simple">
 
<quiz display="simple">
 +
{'''Auf welchem Punkt muss C liegen, damit Du ein stumpfwinkliges Dreieck erzeugst?'''}
 +
-C liegt auf D
 +
+C liegt auf E
 +
+C liegt auf F
 +
 +
 
{'''Ändert sich der <span style="color: blue">Flächeninhalt</span> ?'''}
 
{'''Ändert sich der <span style="color: blue">Flächeninhalt</span> ?'''}
 
-ja
 
-ja
 
+nein
 
+nein
 
</quiz>
 
</quiz>
−
 
 
'''Begründe Deine Antwort!'''
 
'''Begründe Deine Antwort!'''
 +
 +
 
|}
 
|}
 
</div>
 
</div>
Zeile 105: Zeile 113:
 
{|  
 
{|  
 
[[Bild:Ebert_MotivatorHinweis.jpg|100px]]
 
[[Bild:Ebert_MotivatorHinweis.jpg|100px]]
−
*'''Man kann also in einem Dreieck den der Grundseite gegenüberliegenden Punkt <span style="color: green">auf einer Parallelen zur Grundseite wandern</span> lassen, <span style="color: green">ohne dass sich</span> dabei der <span style="color: green">Flächeninhalt</span> des Dreiecks <span style="color: green">ändert</span>. '''
+
*'''Man kann also in einem Dreieck, den Eckpunkt <span style="color: green">auf einer Parallelen zur Grundseite wandern</span> lassen, <span style="color: green">ohne dass sich</span> dabei der <span style="color: green">Flächeninhalt</span> des Dreiecks <span style="color: green">ändert</span>. '''
 
*''' <span style="color: green">Grundseite und Höhe bleiben</span>  dabei immer <span style="color: green">gleich</span>, also auch der <span style="color: green">Flächeninhalt</span>.'''
 
*''' <span style="color: green">Grundseite und Höhe bleiben</span>  dabei immer <span style="color: green">gleich</span>, also auch der <span style="color: green">Flächeninhalt</span>.'''
 
*'''Diesen Bewegungsvorgang nennt man <span style="color: green">Scherung</span>. Du hast dieses Prinzip bereits bei den Parallelogrammen kennen gelernt. '''
 
*'''Diesen Bewegungsvorgang nennt man <span style="color: green">Scherung</span>. Du hast dieses Prinzip bereits bei den Parallelogrammen kennen gelernt. '''

Aktuelle Version vom 17. August 2009, 17:36 Uhr


Variation am Dreieck

Gegeben sind die Seiten:
a =3cm, b= 4cm und c = 5cm

  • Zeig Maja´s Überlegung an


  • Ist nicht schon eine Höhe gegeben? Zeig den Hinweis von Nils an

'

  • Welches spezielle Dreieck ist das Dreieck ABC?

Brauchst Du den Hinweis?

Dreieck ABC ist rechtwinklig
  • Maja hat eine Lösung gefunden
    Ebert MotivatorGrün.jpg

Die Seiten a und b des Dreiecks ABC sind gleichzeitig auch Grundseite und Höhe, da das Dreieck ABC rechtwinklig ist und somit a senkrecht zu b ist.
  • Es gilt zum Beispiel:

Seite b ist Grundseite, damit ist die Länge der Grundseite b 4 (cm)

  • Die Seite a wird damit zur Höhe und da: a = 3 cm

ist der Flächeninhalt des Dreiecks 6(cm²)






Nils hat die Formel für die Berechnung dieses speziellen Dreiecks zusammengefasst:

Ebert MotivatorMerke.jpg Der Flächeninhalt eines rechtwinkligen Dreiecks berechnet sich durch :
Frechtwinklig = {1 \over 2} \cdot b \cdot a

wobei die Seiten a und b senkrecht zueinander stehen.







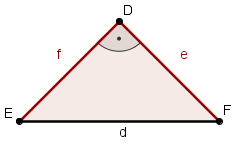
Wie lautet die Flächeninhaltsformel für ein

..gleichschenklig-rechtwinkliges Dreieck EFD ?
Der rechte Winkel befindet sich am Eckpunkt D.
Ebert gleichschenklig.jpg
Ergänze die fehlenden Felder und ermittle daraus die Flächeninhaltsformel für das gleichschenklig-rechtwinklige Dreieck:

1. Flächeninhaltsformel des rechtwinkligen Dreiecks:

Frechtwinklig = {1 \over 2} \cdot e \cdot f

2. Im gleichschenkligen Dreieck gilt für die Seiten f und e:

f = e

\Rightarrow Für den Flächeninhalt F eines rechtwinkligen und gleichschenkligen Dreiecks gilt also zum Beispiel:
F = {1 \over 2} \cdot e \cdot e = {1 \over 2} \cdote²













Flächeninhalt von stumpfwinkligen Dreiecken
  • Ziehe den roten Eckpunkt C auf die Punkte D, E und F.

1. Auf welchem Punkt muss C liegen, damit Du ein stumpfwinkliges Dreieck erzeugst?

C liegt auf D
C liegt auf E
C liegt auf F

2. Ändert sich der Flächeninhalt ?

ja
nein

Punkte: 0 / 0

Begründe Deine Antwort!



Ebert MotivatorHinweis.jpg
  • Man kann also in einem Dreieck, den Eckpunkt auf einer Parallelen zur Grundseite wandern lassen, ohne dass sich dabei der Flächeninhalt des Dreiecks ändert.
  • Grundseite und Höhe bleiben dabei immer gleich, also auch der Flächeninhalt.
  • Diesen Bewegungsvorgang nennt man Scherung. Du hast dieses Prinzip bereits bei den Parallelogrammen kennen gelernt.







Spitze! Du hast die Aufgabe prima bearbeitet

Ebert MotivatorenÜbung.jpg
→Übungsaufgaben zur Flächenberechnung am Dreieck


Hier geht es zurück zur Seite: Zusammenfassung: Flächeninhalt des Dreiecks

Von „http://dmuw.zum.de/index.php?title=Variation_am_Dreieck&oldid=4459“