Die Quadratische Funktion "f(x) = (x - xs)² + ys" - Die Scheitelpunktsform: Unterschied zwischen den Versionen
K (Satzbau Satzzeichen Rechtschreibung) |
K (Kilian Schoeller verschob Seite Lernpfade/Quadratische Funktionen/Die Scheitelpunktsform nach Lernpfade/Quadratische Funktionen/Die Quadratische Funktion "f(x) = (x - xs)² + ys" - Die Scheitelpunktsform, ohne dabei eine Weiterleitung anzulegen…) |
||
| (21 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Lernpfad-M|<big>'''Die Quadratische Funktion "f(x)<math>=</math>(x - x<sub>s</sub>)<sup>2</sup> + y<sub>s</sub>" - Die Scheitelpunktsform'''</big> | {{Lernpfad-M|<big>'''Die Quadratische Funktion "f(x)<math>=</math>(x - x<sub>s</sub>)<sup>2</sup> + y<sub>s</sub>" - Die Scheitelpunktsform'''</big> | ||
| − | + | __NOCACHE__ | |
'''In diesem Lernpfad lernst du die Scheitelpunktsform kennen! Bearbeite den unten aufgeführten Lernpfad''' | '''In diesem Lernpfad lernst du die Scheitelpunktsform kennen! Bearbeite den unten aufgeführten Lernpfad''' | ||
| Zeile 15: | Zeile 15: | ||
| − | Im letzten Lernpfad hast du die quadratische Funktion '''"f(x) = x<sup>2</sup>"''' | + | Im letzten Lernpfad hast du die quadratische Funktion '''"f(x) = x<sup>2</sup>"''' kennengelernt. |
In diesem Lernpfad wollen wir uns mit zwei zusätzlichen Parametern beschäftigen. | In diesem Lernpfad wollen wir uns mit zwei zusätzlichen Parametern beschäftigen. | ||
| Zeile 23: | Zeile 23: | ||
<br> | <br> | ||
{{Merke| | {{Merke| | ||
| − | Die quadratische Funktion '''"f(x)<math>=</math>x<sup>2</sup>"''' ist eine spezielle Parabel. Von ihr | + | Die quadratische Funktion '''"f(x)<math>=</math>x<sup>2</sup>"''' ist eine spezielle Parabel. Von ihr ausgehend werden alle Veränderungen betrachtet und man nennt sie deshalb '''Normalparabel''' |
}} | }} | ||
| Zeile 44: | Zeile 44: | ||
{| {{Prettytable}} | {| {{Prettytable}} | ||
|- style="background-color:#8DB6CD" | |- style="background-color:#8DB6CD" | ||
| − | ! Quadratische Funktion f(x)<math>=</math>x<sup>2</sup>+ y<sub>s</sub> !! Hinweise, Aufgabe und Lückentext: | + | ! Quadratische Funktion "f(x)<math>=</math>x<sup>2</sup>+ y<sub>s</sub>" !! Hinweise, Aufgabe und Lückentext: |
|- | |- | ||
| <ggb_applet height="500" width="350" showResetIcon="true" filename="VerschiebenParametere.ggb" /> || | | <ggb_applet height="500" width="350" showResetIcon="true" filename="VerschiebenParametere.ggb" /> || | ||
| − | '''Hinweise:''' | + | '''Hinweise:''' |
| − | + | ||
| + | * In dem "GeoGebra-Applet" links ist die Normalparabel schwarz-gestrichelt und die von y<sub>s</sub> abhängige, quadratische Funktion blau eingezeichnet | ||
| + | |||
| + | * Bediene mit gehaltener linker Maustaste den schwarzen Schieberegler y<sub>s</sub>, er verändert dessen Wert | ||
| + | |||
| + | * Ziehe im folgenden Lückentext die möglichen Lösungen aus dem blauen Feld, ebenfalls mit gehaltener linker Maustaste, in die richtigen Felder | ||
<br> | <br> | ||
'''Aufgabe:''' <br>Bediene den Schieberegler y<sub>s</sub>. Welche Veränderungen stellst du fest? | '''Aufgabe:''' <br>Bediene den Schieberegler y<sub>s</sub>. Welche Veränderungen stellst du fest? | ||
| Zeile 58: | Zeile 63: | ||
Ist der Parameter y<sub>s</sub> positiv, so wird die Parabel um y '''Einheiten''' in Richtung der y-Achse nach '''oben''' verschoben. <br> | Ist der Parameter y<sub>s</sub> positiv, so wird die Parabel um y '''Einheiten''' in Richtung der y-Achse nach '''oben''' verschoben. <br> | ||
Ist der Parameter y<sub>s</sub> hingegen '''negativ''', so wird die Parabel um y Einheiten in Richtung der '''y-Achse''' nach '''unten''' verschoben. <br> | Ist der Parameter y<sub>s</sub> hingegen '''negativ''', so wird die Parabel um y Einheiten in Richtung der '''y-Achse''' nach '''unten''' verschoben. <br> | ||
| − | Der '''Scheitelpunkt''' der Parabel befindet sich auf der y-Achse, genauer gesagt bei Punkt '''[0 | + | Der '''Scheitelpunkt''' der Parabel befindet sich auf der y-Achse, genauer gesagt bei Punkt '''[0| y<sub>s</sub>]'''. Zudem ist die y-Achse die '''Symmetrieachse''' der Parabel. |
| − | + | ||
</div> | </div> | ||
|} | |} | ||
| Zeile 71: | Zeile 76: | ||
* Für '''y<sub>s</sub> > 0''' gilt: Verschiebung um y Einheiten nach '''oben''' | * Für '''y<sub>s</sub> > 0''' gilt: Verschiebung um y Einheiten nach '''oben''' | ||
* Für '''y<sub>s</sub> < 0''' gilt: Verschiebung um y Einheiten nach '''unten''' | * Für '''y<sub>s</sub> < 0''' gilt: Verschiebung um y Einheiten nach '''unten''' | ||
| − | * Der '''Scheitelpunkt''' liegt bei '''S (0 | + | * Der '''Scheitelpunkt''' liegt bei '''S (0, y<sub>s</sub>)''' |
* Die y-Achse ist '''Symmetrieachse''' | * Die y-Achse ist '''Symmetrieachse''' | ||
}} | }} | ||
| Zeile 154: | Zeile 159: | ||
| || <u> Funktionsgleichung </u> || <u> Scheitelpunkt </u> | | || <u> Funktionsgleichung </u> || <u> Scheitelpunkt </u> | ||
|- | |- | ||
| − | | 1. || y<math>=</math> x<sup>2</sup> + 5,2 || <strong> S [0 | + | | 1. || y<math>=</math> x<sup>2</sup> + 5,2 || <strong> S <math>[0|5,2]</math> </strong> <br> |
|- | |- | ||
| − | | 2. || y<math>=</math> 3 + x<sup>2</sup> || <strong> S [0 | + | | 2. || y<math>=</math> 3 + x<sup>2</sup> || <strong> S <math>[0|3]</math> </strong> |
|- | |- | ||
| − | | 3. || y<math>=</math> x<sup>2</sup> - 3 || <strong> S [0 | + | | 3. || y<math>=</math> x<sup>2</sup> - 3 || <strong> S <math>[0|-3]</math> </strong> <br> |
|- | |- | ||
| − | | 4. || y<math>=</math> x<sup>2</sup> || <strong> S [0 | + | | 4. || y<math>=</math> x<sup>2</sup> || <strong> S <math>[0|0]</math> </strong> <br> |
|} | |} | ||
</div> | </div> | ||
| Zeile 169: | Zeile 174: | ||
{| {{Prettytable}} | {| {{Prettytable}} | ||
|- style="background-color:#8DB6CD" | |- style="background-color:#8DB6CD" | ||
| − | ! Aufgabe !! Quadratische Funktion f(x)<math>=</math>x<sup>2</sup>+ y<sub>s</sub> | + | ! Aufgabe !! Quadratische Funktion "f(x)<math>=</math>x<sup>2</sup>+ y<sub>s</sub>" |
|- | |- | ||
|Gegeben sind fünf Funktionsgleichungen, sowie fünf verschiedene Koordinaten.<br> Finde zu jeder Funktionsgleichung den Punkt, der auf ihrer Parabel liegt. | |Gegeben sind fünf Funktionsgleichungen, sowie fünf verschiedene Koordinaten.<br> Finde zu jeder Funktionsgleichung den Punkt, der auf ihrer Parabel liegt. | ||
| Zeile 184: | Zeile 189: | ||
{| | {| | ||
|- | |- | ||
| − | | 1. || y <math>=</math> x<sup>2</sup> - 1 || <strong> [3 | + | | 1. || y <math>=</math> x<sup>2</sup> - 1 || <strong> <math>[3|8]</math> </strong> <br> |
|- | |- | ||
| − | | 2. || y <math>=</math> x<sup>2</sup> - 5 || <strong> [3 | + | | 2. || y <math>=</math> x<sup>2</sup> - 5 || <strong> <math>[3|4]</math> </strong> <br> |
|- | |- | ||
| − | | 3. || y <math>=</math> x<sup>2</sup> + 0 || <strong> [2 | + | | 3. || y <math>=</math> x<sup>2</sup> + 0 || <strong> <math>[2|4]</math> </strong> <br> |
|- | |- | ||
| − | | 4. || y <math>=</math> x<sup>2</sup> + 2 || <strong> [1 | + | | 4. || y <math>=</math> x<sup>2</sup> + 2 || <strong> <math>[1|3]</math> </strong> <br> |
|- | |- | ||
| − | | 5. || y <math>=</math> x<sup>2</sup> + 4 || <strong> [2 | + | | 5. || y <math>=</math> x<sup>2</sup> + 4 || <strong> <math>[2|8]</math> </strong> <br> |
|} | |} | ||
</div> | </div> | ||
| − | Überprüfe dein Ergebnis mit dem Applet rechts.<br> Verschiebe dafür die Parabel entsprechend der Funktionsgleichung. | + | Überprüfe dein Ergebnis mit dem "GeoGebra-Applet" rechts.<br> Verschiebe dafür die Parabel entsprechend der Funktionsgleichung. |
|| | || | ||
| Zeile 223: | Zeile 228: | ||
Mit Hilfe des Schiebereglers x<sub>s</sub> stellt man fest, dass für positive Werte eine Verschiebung um '''x-Einheiten''' nach '''rechts''' erfolgt. Ist der Wert von x<sub>s</sub> '''negativ''', so wird der Graph um x-Einheiten nach '''links''' verschoben. | Mit Hilfe des Schiebereglers x<sub>s</sub> stellt man fest, dass für positive Werte eine Verschiebung um '''x-Einheiten''' nach '''rechts''' erfolgt. Ist der Wert von x<sub>s</sub> '''negativ''', so wird der Graph um x-Einheiten nach '''links''' verschoben. | ||
<br> | <br> | ||
| − | Aber Achtung! Es wird ein kleines Verwirrspiel getrieben, denn für positive x-Werte lautet die Funktionsgleichung "f(x) = '''[x - x<sub>s</sub>]<sup>2</sup>'''". Man macht leicht den Fehler und stellt für positve Werte die Gleichung "f(x) = [x + x<sub>s</sub>]<sup>2</sup>" auf. Da die Funktionsgleichung jedoch "f(x) = (x - x<sub>s</sub>)<sup>2</sup>" lautet, entsteht für positive Werte eine '''Differenz''' in der Klammer. Genau andersherum verhält es sich für negative Werte von x<sub>s</sub>, denn dort lautet die Funktionsgleichung "f(x) = '''[x + x<sub>s</sub>]<sup>2</sup>'''". | + | Aber Achtung! Es wird ein kleines Verwirrspiel getrieben, denn für positive x-Werte lautet die Funktionsgleichung "f(x) = '''[x - x<sub>s</sub>]<sup>2</sup>'''". Man macht leicht den Fehler und stellt für positve Werte die Gleichung "f(x) = [x + x<sub>s</sub>]<sup>2</sup>" auf. Da die Funktionsgleichung jedoch "f(x) = (x - x<sub>s</sub>)<sup>2</sup>" lautet, entsteht für positive Werte eine '''Differenz''' in der Klammer. Genau andersherum verhält es sich für negative Werte von x<sub>s</sub>, denn dort lautet die Funktionsgleichung "f(x) = '''[x + x<sub>s</sub>]<sup>2</sup>'''". Der Scheitelpunkt liegt im Punkt "S '''[x<sub>s</sub>|0]'''", denn der y-Wert bleibt '''Null'''. |
Die Symmetrieachse ist die Parallelachse zur y-Achse senkrecht zur '''x-Achse'''. | Die Symmetrieachse ist die Parallelachse zur y-Achse senkrecht zur '''x-Achse'''. | ||
</div> | </div> | ||
| Zeile 238: | Zeile 243: | ||
* Für '''x<sub>s</sub> > 0''' gilt: Verschiebung um x Einheiten nach '''rechts''' | * Für '''x<sub>s</sub> > 0''' gilt: Verschiebung um x Einheiten nach '''rechts''' | ||
* Für '''x<sub>s</sub> < 0''' gilt: Verschiebung um x Einheiten nach '''links''' | * Für '''x<sub>s</sub> < 0''' gilt: Verschiebung um x Einheiten nach '''links''' | ||
| − | * Der '''Scheitelpunkt''' liegt bei '''S | + | * Der '''Scheitelpunkt''' liegt bei '''S (x<sub>s</sub>, 0)''' |
* Die '''Symmetrieachse''' ist die Parallelachse zur y-Achse, senkrecht zur x-Achse | * Die '''Symmetrieachse''' ist die Parallelachse zur y-Achse, senkrecht zur x-Achse | ||
}} | }} | ||
| Zeile 320: | Zeile 325: | ||
<big>'''3. Aufgabe:'''</big> | <big>'''3. Aufgabe:'''</big> | ||
| − | Du siehst im | + | Du siehst im folgenden Koordinatensystem drei Parabeln. Man kann diese drei Parabeln durch Bedienen der Schieberegler verschieben. Verschiebe die drei Parabeln so, dass sie den Platz für die folgenden Funktionsgleichungen einnehmen. |
f(x) = (x - 2)<sup>2</sup> | f(x) = (x - 2)<sup>2</sup> | ||
| Zeile 326: | Zeile 331: | ||
f(x) = (x + 3)<sup>2</sup> | f(x) = (x + 3)<sup>2</sup> | ||
| − | Überprüfe | + | Überprüfe anschließend durch Anklicken des Kontrollkästchens, ob du die Aufgabe richtig gelöst hast. Überdecken die blau-gestrichelten Parabeln deine verschobenen Parabeln, dann hast du die Aufgabe richtig gelöst. |
<div align="center"><ggb_applet height="480" width="620" showResetIcon="true" filename="Für_Lernpfad_2_Station_3_Aufgabe_3.ggb" /></div> | <div align="center"><ggb_applet height="480" width="620" showResetIcon="true" filename="Für_Lernpfad_2_Station_3_Aufgabe_3.ggb" /></div> | ||
| Zeile 337: | Zeile 342: | ||
Bevor wir nun die beiden Parameter y<sub>s</sub> und x<sub>s</sub> zusammenführen, wollen wir die wichtigsten Eigenschaften wiederholen. Löse dafür die folgende Zuordnung. | Bevor wir nun die beiden Parameter y<sub>s</sub> und x<sub>s</sub> zusammenführen, wollen wir die wichtigsten Eigenschaften wiederholen. Löse dafür die folgende Zuordnung. | ||
| − | Mal sehen wer am wenigstens Versuche braucht! | + | Mal sehen, wer am wenigstens Versuche braucht! |
| Zeile 347: | Zeile 352: | ||
| || <u> Frage </u> || <u> Antwort </u> | | || <u> Frage </u> || <u> Antwort </u> | ||
|- | |- | ||
| − | | 1. || Wie lautet der Scheitelpunkt für y<math>=</math> [x - 2]<sup>2</sup>? || <strong>S [2 | + | | 1. || Wie lautet der Scheitelpunkt für "y<math>=</math> [x - 2]<sup>2</sup>"? || <strong>S <math>[2|0]</math> </strong> <br> |
|- | |- | ||
| 2. || Wie lautet die Funktionsgleichung für eine Verschiebung nach unten auf der y-Achse? || <strong>y<math>=</math> x<sup>2</sup> - y<sub>s</sub></strong> | | 2. || Wie lautet die Funktionsgleichung für eine Verschiebung nach unten auf der y-Achse? || <strong>y<math>=</math> x<sup>2</sup> - y<sub>s</sub></strong> | ||
|- | |- | ||
| − | | 3. || Wie lautet der Scheitelpunkt für y<math>=</math> x<sup>2</sup> - 4? || <strong>S [0 | + | | 3. || Wie lautet der Scheitelpunkt für "y<math>=</math> x<sup>2</sup> - 4"? || <strong>S <math>[0|-4]</math> </strong> |
|- | |- | ||
| 4. || Wie lautet die Funktionsgleichung für eine Verschiebung nach links auf der x-Achse? || <strong>y<math>=</math> [x + x<sub>s</sub>]<sup>2</sup></strong> | | 4. || Wie lautet die Funktionsgleichung für eine Verschiebung nach links auf der x-Achse? || <strong>y<math>=</math> [x + x<sub>s</sub>]<sup>2</sup></strong> | ||
|- | |- | ||
| − | | 5. || Wie lautet der Scheitelpunkt für y<math>=</math> x<sup>2</sup> + 2? || <strong>S [0 | + | | 5. || Wie lautet der Scheitelpunkt für "y<math>=</math> x<sup>2</sup> + 2"? || <strong>S <math>[0|2]</math> </strong> |
|- | |- | ||
| 6. || Wie lautet die Funktionsgleichung für eine Verschiebung nach rechts auf der x-Achse? || <strong>y<math>=</math> [x - x<sub>s</sub>]<sup>2</sup></strong> | | 6. || Wie lautet die Funktionsgleichung für eine Verschiebung nach rechts auf der x-Achse? || <strong>y<math>=</math> [x - x<sub>s</sub>]<sup>2</sup></strong> | ||
| Zeile 361: | Zeile 366: | ||
| 7. || Wie lautet die Funktionsgleichung für eine Verschiebung nach oben auf der y-Achse? || <strong>y<math>=</math> x<sup>2</sup> + y<sub>s</sub></strong> | | 7. || Wie lautet die Funktionsgleichung für eine Verschiebung nach oben auf der y-Achse? || <strong>y<math>=</math> x<sup>2</sup> + y<sub>s</sub></strong> | ||
|- | |- | ||
| − | | 8. || Wie lautet der Scheitelpunkt für y<math>=</math> [x + 4]<sup>2</sup>? || <strong>S [-4 | + | | 8. || Wie lautet der Scheitelpunkt für "y<math>=</math> [x + 4]<sup>2</sup>"? || <strong>S <math>[-4|0]</math> </strong> |
|} | |} | ||
| Zeile 384: | Zeile 389: | ||
Jetzt sind wir an einem Punkt angekommen, an dem wir die Scheitelpunktsform aufstellen können. | Jetzt sind wir an einem Punkt angekommen, an dem wir die Scheitelpunktsform aufstellen können. | ||
| − | In dieser Lerneinheit hast du die Parameter y<sub>s</sub> und x<sub>s</sub> einzeln | + | In dieser Lerneinheit hast du die Parameter y<sub>s</sub> und x<sub>s</sub> einzeln kennengelernt. |
<br><br> | <br><br> | ||
Ziel dieser Lerneinheit ist die quadratische Funktion '''"f(x) = (x - x<sub>s</sub>)<sup>2</sup> + y<sub>s</sub>"''', in der beide Parameter integriert sind. | Ziel dieser Lerneinheit ist die quadratische Funktion '''"f(x) = (x - x<sub>s</sub>)<sup>2</sup> + y<sub>s</sub>"''', in der beide Parameter integriert sind. | ||
| Zeile 398: | Zeile 403: | ||
{| {{Prettytable}} | {| {{Prettytable}} | ||
|- style="background-color:#8DB6CD" | |- style="background-color:#8DB6CD" | ||
| − | ! Quadratische Funktion f(x)<math>=</math>(x - x<sub>s</sub>)<sup>2</sup> + y<sub>s</sub> !! Hinweise und Quiz: | + | ! Quadratische Funktion "f(x)<math>=</math>(x - x<sub>s</sub>)<sup>2</sup> + y<sub>s</sub>"!! Hinweise und Quiz: |
|- | |- | ||
| <ggb_applet height="500" width="350" showResetIcon="true" filename="VerschiebenParameterdunde.ggb" /> || | | <ggb_applet height="500" width="350" showResetIcon="true" filename="VerschiebenParameterdunde.ggb" /> || | ||
| − | '''Hinweise:''' | + | '''Hinweise:''' |
| − | + | ||
| − | + | * In dem "GeoGebra-Applet" siehst du die verschobene Normalparabel | |
| + | |||
| + | * Mit den Schiebereglern y<sub>s</sub> und x<sub>s</sub> kannst du die Lage der Parabel verändern | ||
| + | |||
| + | * Bediene die Schieberegler und versuche das folgende Quiz zu lösen | ||
<br> | <br> | ||
| Zeile 437: | Zeile 446: | ||
{{Merke| | {{Merke| | ||
| − | Für die quadratische Funktion '''f(x)<math>=</math>(x - x<sub>s</sub>)<sup>2</sup> + y<sub>s</sub>''' gilt: | + | Für die quadratische Funktion '''"f(x)<math>=</math>(x - x<sub>s</sub>)<sup>2</sup> + y<sub>s</sub>"''' gilt: |
* Der Graph der Funktion ist eine '''verschobene''' Parabel in der '''Ebene''' | * Der Graph der Funktion ist eine '''verschobene''' Parabel in der '''Ebene''' | ||
* Die Parabel ist '''kongruent''' zur Normalparabel | * Die Parabel ist '''kongruent''' zur Normalparabel | ||
* Man erhält den Graph von f durch verschieben der Normalparabel um '''x Einheiten''' entlang der '''x-Achse''' und um '''y Einheiten''' entlang der '''y-Achse''' | * Man erhält den Graph von f durch verschieben der Normalparabel um '''x Einheiten''' entlang der '''x-Achse''' und um '''y Einheiten''' entlang der '''y-Achse''' | ||
| − | * Der '''Scheitelpunkt''' liegt bei S | + | * Der '''Scheitelpunkt''' liegt bei '''S (x<sub>s</sub>, y<sub>s</sub>)''' |
| − | * Die '''Symmetrieachse''' hat die Gleichung x <math>=</math> y<sub>s</sub> | + | * Die '''Symmetrieachse''' hat die Gleichung '''"x <math>=</math> y<sub>s</sub>"''' |
}} | }} | ||
| Zeile 458: | Zeile 467: | ||
<div class="multiplechoice-quiz"> | <div class="multiplechoice-quiz"> | ||
| − | '''f(x) <math>=</math> (x - 5)<sup>2</sup> - 3''' (!Die Parabel ist nach rechts und nach oben verschoben)(!Die Parabel hat den Scheitelpunkt S [-3 | + | '''"f(x) <math>=</math> (x - 5)<sup>2</sup> - 3"''' (!Die Parabel ist nach rechts und nach oben verschoben)(!Die Parabel hat den Scheitelpunkt S <math>[-3|5]</math>)(Die Parabel hat den Scheitelpunkt S <math>[5|-3]</math>) (!Die Parabel ist nach unten geöffnet) (Die Parabel ist nach rechts und nach unten verschoben) |
| − | '''f(x) <math>=</math> 5 + (x + 12)<sup>2</sup>''' (!Es liegt keine Parabel vor) (Die Parabel ist um 5 Einheiten nach oben verschoben) (!Die Parabel ist um 12 Einheiten nach rechts verschoben) (Die Parabel ist um 12 Einheiten nach links verschoben) (Die Parabel liegt oberhalb der x-Achse) (!Die Parabel hat keine Symmetrieachse) | + | '''"f(x) <math>=</math> 5 + (x + 12)<sup>2</sup>"''' (!Es liegt keine Parabel vor) (Die Parabel ist um 5 Einheiten nach oben verschoben) (!Die Parabel ist um 12 Einheiten nach rechts verschoben) (Die Parabel ist um 12 Einheiten nach links verschoben) (Die Parabel liegt oberhalb der x-Achse) (!Die Parabel hat keine Symmetrieachse) |
| − | '''f(x) <math>=</math> x<sup>2</sup> + 3''' (!Die Parabel ist eine um 3 Einheiten nach links verschobene Normalparabel) (Die Parabel hat den Scheitelpunkt [0 | + | '''"f(x) <math>=</math> x<sup>2</sup> + 3"''' (!Die Parabel ist eine um 3 Einheiten nach links verschobene Normalparabel) (Die Parabel hat den Scheitelpunkt S <math>[0|3]</math>) (Die Symmetrieachse der Parabel ist die y-Achse) (!Die Parabel ist um eine Einheit nach rechts verschoben) (Die Parabel ist nach oben geöffnet) |
| − | '''f(x) <math>=</math>-5 + (x - 6)<sup>2</sup>''' (!Die Funktionsgleichung ist keine quadratische Funktion) (!Die Parabel ist um 5 Einheiten nach links verschoben) (Die Parabel ist um 6 Einheiten nach rechts verschoben) (Die Parabel ist um 5 Einheiten nach unten verschoben) (! Die Parabel ist um 5 Einheiten nach unten und um 6 Einheiten nach links veschoben) | + | '''"f(x) <math>=</math>-5 + (x - 6)<sup>2</sup>"''' (!Die Funktionsgleichung ist keine quadratische Funktion) (!Die Parabel ist um 5 Einheiten nach links verschoben) (Die Parabel ist um 6 Einheiten nach rechts verschoben) (Die Parabel ist um 5 Einheiten nach unten verschoben) (! Die Parabel ist um 5 Einheiten nach unten und um 6 Einheiten nach links veschoben) |
</div> | </div> | ||
Aktuelle Version vom 5. Dezember 2018, 22:54 Uhr
|
Lernpfad
|
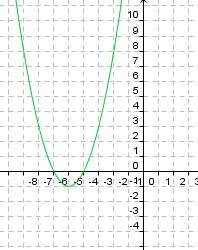
Im letzten Lernpfad hast du die quadratische Funktion "f(x) = x2" kennengelernt.
In diesem Lernpfad wollen wir uns mit zwei zusätzlichen Parametern beschäftigen.
Bevor wir beginnen, soll zunächst noch ein neuer Begriff eingeführt werden, da dieser später häufiger verwendet wird.
30px Merke
Die quadratische Funktion "f(x) |
Zunächst betrachten wir den Parameter ys, welcher zur quadratischen Funktion "f(x) = x2" dazuaddiert wird. Die quadratische Funktion schaut dann wie folgt aus:
f(x) = x2 + ys
Bearbeite das folgende Arbeitsblatt und entdecke die Eigenschaften vom Parameter ys!
Quadratische Funktion "f(x) x2+ ys" x2+ ys" |
Hinweise, Aufgabe und Lückentext: |
|---|---|
|
Hinweise:
Der Parameter ys verschiebt die Normalparabel auf der y-Achse. Dabei bleibt die verschobene Parabel kongruent zur Normalparabel. |
30px Merke
Für die quadratische Funktion "f(x)
|
Es folgen nun einige Aufgaben, um das gerade erlernte Wissen zu vertiefen.
1. Aufgabe: Zuordnung
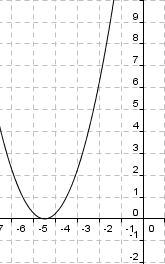
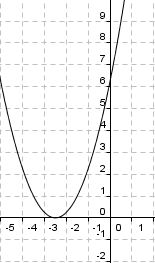
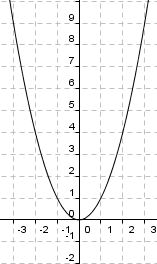
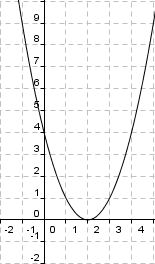
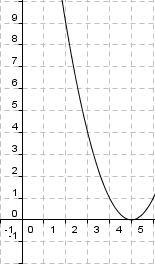
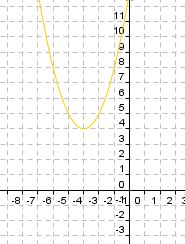
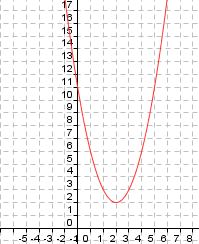
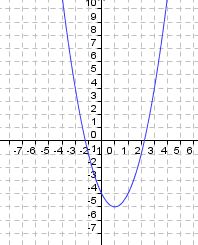
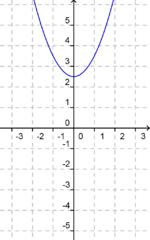
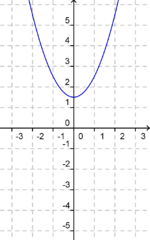
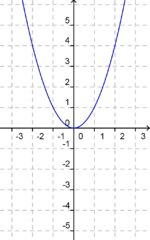
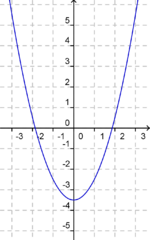
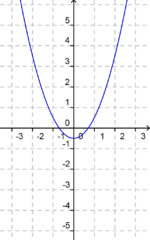
Du siehst hier fünf verschiedene Graphen der quadratischen Funktion "f(x) = x2 + ys". Ermittle zu den vorgegebenen Graphen die passende Funktionsgleichung. Falls du Probleme hast, betrachte nochmals die Veränderungen des oben aufgeführten Graphen.
2. Aufgabe:
Bestimme mit Hilfe der vorgegebenen Scheitelpunkte die Funktionsgleichung. Ordne dann die entsprechende Funktionsgleichung dem jeweiligen Scheitelpunkt zu!
| Scheitelpunkt | Funktionsgleichung | |
| 1. | S 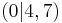 |
y x2 + 4,7 x2 + 4,7 |
| 2. | S 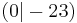 |
y x2 - 23 x2 - 23 |
| 3. | S 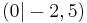 |
y x2 - 2,5 x2 - 2,5 |
| 4. | S 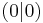 |
y x2 x2 |
| 5. | S 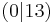 |
y x2 + 13 x2 + 13
|
3. Aufgabe:
Nun hast du die Funktionsgleichung gegeben. Finde jetzt den zugehörigen Scheitelpunkt S.
| Funktionsgleichung | Scheitelpunkt | |
| 1. | y x2 + 5,2 x2 + 5,2 |
S ![[0|5,2]](/images/math/a/4/9/a49ca3d0f18380b0ccfca1927be6815d.png) |
| 2. | y 3 + x2 3 + x2 |
S ![[0|3]](/images/math/5/7/b/57b3ff3f535629765ed30c1f5dbf9825.png)
|
| 3. | y x2 - 3 x2 - 3 |
S ![[0|-3]](/images/math/0/1/1/011af7b21e1e7a96c15acaa22a7aa0c7.png) |
| 4. | y x2 x2 |
S ![[0|0]](/images/math/a/d/4/ad48623e3f482606eeea6e8faee14a0b.png) |
4. Aufgabe: Zuordnung
| Aufgabe | Quadratische Funktion "f(x) x2+ ys" x2+ ys"
| |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Gegeben sind fünf Funktionsgleichungen, sowie fünf verschiedene Koordinaten. Finde zu jeder Funktionsgleichung den Punkt, der auf ihrer Parabel liegt.
Hilfe: Es liegt nur dann ein Punkt auf der Parabel,
|
|
Nachdem du jetzt den Parameter ys kennst, wollen wir uns mit dem Parameter xs beschäftigen. Er wird in die quadratische Funktion wie folgt integriert:
f(x) = (x - xs)2
Um die Eigenschaften dieses Parameters zu erlernen, bediene den Schieberegler xs in der nachfolgenden Geogebraanwendung, er verändert dessen Wert. Die schwarz-gestrichelte Parabel ist die Normalparabel. Löse anschließend den darauf folgenden Lückentext und ziehe hierfür die richtigen Textbausteine, mit gehaltener linker Maustaste, in die Lücken.
Lückentext! - Ordne die richtigen Begriffe zu:
Der Parameter xs der quadratischen Funktion "f(x) = (x - xs)2" bewirkt eine Verschiebung der Normalparabel auf der x-Achse. Wie schon bei der Verschiebumg des Parameters ys, ist die verschobene Parabel kongruent zur Normalparabel.
Mit Hilfe des Schiebereglers xs stellt man fest, dass für positive Werte eine Verschiebung um x-Einheiten nach rechts erfolgt. Ist der Wert von xs negativ, so wird der Graph um x-Einheiten nach links verschoben.
Aber Achtung! Es wird ein kleines Verwirrspiel getrieben, denn für positive x-Werte lautet die Funktionsgleichung "f(x) = [x - xs]2". Man macht leicht den Fehler und stellt für positve Werte die Gleichung "f(x) = [x + xs]2" auf. Da die Funktionsgleichung jedoch "f(x) = (x - xs)2" lautet, entsteht für positive Werte eine Differenz in der Klammer. Genau andersherum verhält es sich für negative Werte von xs, denn dort lautet die Funktionsgleichung "f(x) = [x + xs]2". Der Scheitelpunkt liegt im Punkt "S [xs|0]", denn der y-Wert bleibt Null.
Die Symmetrieachse ist die Parallelachse zur y-Achse senkrecht zur x-Achse.
Das waren einige wichtige Erkenntnisse, die wir nachfolgend festhalten wollen!
30px Merke
Für die quadratische Funktion "f(x)
|
Achtung!
- Für xs > 0, mit einer Verschiebung nach rechts, lautet die Funktionsgleichung "f(x) = (x – xs)2"
Beispiel: Für xs = 5: f(x) = (x - 5)2
- Für xs < 0, mit einer Verschiebung nach links, lautet die Funktionsgleichung "f(x) = (x + xs)2"
Beispiel: Für xs = -5: f(x) = (x + 5)2
Ebenso wie beim Parameter ys, folgen wieder einige Aufgaben, um auch diese Eigenschaften zu vertiefen.
1. Aufgabe: Zuordnung
Gegeben sind die Graphen fünf verschiedener quadratischer Funktionen. Ordne jedem Graph die richtige Funktionsgleichung durch "drag and drop" zu:
2. Aufgabe:
Bestimme mit Hilfe der vorgegebenen Scheitelpunkte die Funktionsgleichung. Ordne dann die entsprechende Funktionsgleichung dem jeweiligen Scheitelpunkt zu!
| Scheitelpunkt | Funktionsgleichung | |
| 1. | S 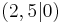 |
y [x - 2,5]2 [x - 2,5]2 |
| 2. | S 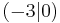 |
y [x + 3]2 [x + 3]2 |
| 3. | S 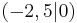 |
y [x + 2,5]2 [x + 2,5]2 |
| 4. | S 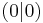 |
y x2 x2 |
| 5. | S 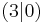 |
y [x - 3]2 [x - 3]2
|
3. Aufgabe:
Du siehst im folgenden Koordinatensystem drei Parabeln. Man kann diese drei Parabeln durch Bedienen der Schieberegler verschieben. Verschiebe die drei Parabeln so, dass sie den Platz für die folgenden Funktionsgleichungen einnehmen.
f(x) = (x - 2)2
f(x) = (x - 5)2
f(x) = (x + 3)2
Überprüfe anschließend durch Anklicken des Kontrollkästchens, ob du die Aufgabe richtig gelöst hast. Überdecken die blau-gestrichelten Parabeln deine verschobenen Parabeln, dann hast du die Aufgabe richtig gelöst.
Bevor wir nun die beiden Parameter ys und xs zusammenführen, wollen wir die wichtigsten Eigenschaften wiederholen. Löse dafür die folgende Zuordnung.
Mal sehen, wer am wenigstens Versuche braucht!
| Frage | Antwort | |
| 1. | Wie lautet der Scheitelpunkt für "y [x - 2]2"? [x - 2]2"? |
S ![[2|0]](/images/math/b/7/6/b76b8b0f71de4f9a6105c4520d4c7929.png) |
| 2. | Wie lautet die Funktionsgleichung für eine Verschiebung nach unten auf der y-Achse? | y x2 - ys x2 - ys
|
| 3. | Wie lautet der Scheitelpunkt für "y x2 - 4"? x2 - 4"? |
S ![[0|-4]](/images/math/9/5/c/95c114a6acc81c60f8c08987a27451cc.png)
|
| 4. | Wie lautet die Funktionsgleichung für eine Verschiebung nach links auf der x-Achse? | y [x + xs]2 [x + xs]2
|
| 5. | Wie lautet der Scheitelpunkt für "y x2 + 2"? x2 + 2"? |
S ![[0|2]](/images/math/a/4/2/a427a1d2ecb73136023bfde799cdff7f.png)
|
| 6. | Wie lautet die Funktionsgleichung für eine Verschiebung nach rechts auf der x-Achse? | y [x - xs]2 [x - xs]2
|
| 7. | Wie lautet die Funktionsgleichung für eine Verschiebung nach oben auf der y-Achse? | y x2 + ys x2 + ys
|
| 8. | Wie lautet der Scheitelpunkt für "y [x + 4]2"? [x + 4]2"? |
S ![[-4|0]](/images/math/0/8/a/08aae5d43ff17c2ed2d83aa4985f0ae7.png)
|
Jetzt sind wir an einem Punkt angekommen, an dem wir die Scheitelpunktsform aufstellen können.
In dieser Lerneinheit hast du die Parameter ys und xs einzeln kennengelernt.
Ziel dieser Lerneinheit ist die quadratische Funktion "f(x) = (x - xs)2 + ys", in der beide Parameter integriert sind.
Du weißt mittlerweile, welche Aufgaben der jeweilige Parameter hat.
Während der Parameter ys für den y-Wert im Koordinatensystem steht, gibt der Parameter xs den x-Wert an. Genau durch diese beiden Punkte wird der Scheitelpunkt der Parabel bestimmt und man nennt die quadratische Funktion "f(x) = (x - xs)2 + ys" deshalb Scheitelpunktsform.
Die Scheitelpunktsform vereint somit die Eigenschaften der Paramter xs und ys.
Im folgenden Kreuzworträtsel werden diese Eigenschaften nun noch mal abgefragt. Viel Erfolg!
Quadratische Funktion "f(x) (x - xs)2 + ys" (x - xs)2 + ys" |
Hinweise und Quiz: | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Hinweise:
Quiz: Beim Klick auf die Ziffern im Kreuzworträtsel öffnet sich ein Eingabefeld. Trage dort deine Antwort ein. In deiner Lösung dürfen keine Bindestriche vorkommen, z.B. für die x-Achse schreibt man xAchse. Erst wenn das komplette Rätsel ausgefüllt ist, können die Ergebnisse überprüft werden.
|
30px Merke
Für die quadratische Funktion "f(x)
|
1. Aufgabe: Multiple Choice
Kreuze alle richtigen Aussagen an!
"f(x)  (x - 5)2 - 3" (!Die Parabel ist nach rechts und nach oben verschoben)(!Die Parabel hat den Scheitelpunkt S
(x - 5)2 - 3" (!Die Parabel ist nach rechts und nach oben verschoben)(!Die Parabel hat den Scheitelpunkt S ![[-3|5]](/images/math/6/4/c/64c97c0ba3438f5d938a577dc2eecea1.png) )(Die Parabel hat den Scheitelpunkt S
)(Die Parabel hat den Scheitelpunkt S ![[5|-3]](/images/math/b/2/a/b2a8b2f4025095a80c3d25efc6387d3c.png) ) (!Die Parabel ist nach unten geöffnet) (Die Parabel ist nach rechts und nach unten verschoben)
) (!Die Parabel ist nach unten geöffnet) (Die Parabel ist nach rechts und nach unten verschoben)
"f(x)  5 + (x + 12)2" (!Es liegt keine Parabel vor) (Die Parabel ist um 5 Einheiten nach oben verschoben) (!Die Parabel ist um 12 Einheiten nach rechts verschoben) (Die Parabel ist um 12 Einheiten nach links verschoben) (Die Parabel liegt oberhalb der x-Achse) (!Die Parabel hat keine Symmetrieachse)
5 + (x + 12)2" (!Es liegt keine Parabel vor) (Die Parabel ist um 5 Einheiten nach oben verschoben) (!Die Parabel ist um 12 Einheiten nach rechts verschoben) (Die Parabel ist um 12 Einheiten nach links verschoben) (Die Parabel liegt oberhalb der x-Achse) (!Die Parabel hat keine Symmetrieachse)
"f(x)  x2 + 3" (!Die Parabel ist eine um 3 Einheiten nach links verschobene Normalparabel) (Die Parabel hat den Scheitelpunkt S
x2 + 3" (!Die Parabel ist eine um 3 Einheiten nach links verschobene Normalparabel) (Die Parabel hat den Scheitelpunkt S ![[0|3]](/images/math/5/7/b/57b3ff3f535629765ed30c1f5dbf9825.png) ) (Die Symmetrieachse der Parabel ist die y-Achse) (!Die Parabel ist um eine Einheit nach rechts verschoben) (Die Parabel ist nach oben geöffnet)
) (Die Symmetrieachse der Parabel ist die y-Achse) (!Die Parabel ist um eine Einheit nach rechts verschoben) (Die Parabel ist nach oben geöffnet)
"f(x)  -5 + (x - 6)2" (!Die Funktionsgleichung ist keine quadratische Funktion) (!Die Parabel ist um 5 Einheiten nach links verschoben) (Die Parabel ist um 6 Einheiten nach rechts verschoben) (Die Parabel ist um 5 Einheiten nach unten verschoben) (! Die Parabel ist um 5 Einheiten nach unten und um 6 Einheiten nach links veschoben)
-5 + (x - 6)2" (!Die Funktionsgleichung ist keine quadratische Funktion) (!Die Parabel ist um 5 Einheiten nach links verschoben) (Die Parabel ist um 6 Einheiten nach rechts verschoben) (Die Parabel ist um 5 Einheiten nach unten verschoben) (! Die Parabel ist um 5 Einheiten nach unten und um 6 Einheiten nach links veschoben)
2. Aufgabe:
Gegeben ist der Scheitelpunkt S einer verschobenen Normalparabel. Finde zum jeweiligen Scheitelpunkt die richtige Funktionsvorschrift:
| Scheitelpunkt | Funktionsgleichung | |
| 1. | S 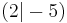 |
y [x - 2]2 - 5 [x - 2]2 - 5 |
| 2. | S 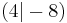 |
y [x - 4]2 - 8 [x - 4]2 - 8 |
| 3. | S 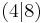 |
y [x - 4]2 + 8 [x - 4]2 + 8 |
| 4. | S 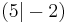 |
y [x - 5]2 - 2 [x - 5]2 - 2 |
3. Aufgabe-Zuordnung:
Finde die richtige Funktionsvorschrift für die Graphen!
4. Aufgabe: KNIFFELAUFGABE:
Zum Abschluss dieser Lektion noch eine kleine Aufgabe zum Nachdenken.
Gegeben ist die Funktion "f(x) = (x + 3)2 + 1,5" und die Punkte W, X, T und P.
Welche dieser Punkte liegt auf dem Graph? Überprüfe dies durch Kopfrechnung!
a) Wb) X
c) T
d) P
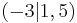
Hilfe:
Falls du nicht weiterkommst, lass dir helfen!
Bediene nun den Schieberegler, um den Graph der Funktion an die richtige Stelle zu positionieren. Mit dem Anklicken des Kontrollkästchens "Punkte an", erkennst du, welche Punkte auf der Parabel liegen.
Prima!
Damit kennst du nun die Parameter xs und ys, welche für die Verschiebung der Parabel in der Ebene verantwortlich sind.
In der nächsten Lerneinheit lernst du dann die Normalform kennen.
![[3|8]](/images/math/3/8/a/38a44163c1c69907273b259c6343f0d8.png)
![[3|4]](/images/math/6/a/2/6a25000dec37ff9fc221343d3c39877a.png)
![[2|4]](/images/math/a/1/5/a15d59ec7583e2154cd05d176c0b2e9e.png)
![[1|3]](/images/math/a/4/f/a4f5768ba5587302d2818a67a3fba30e.png)
![[2|8]](/images/math/f/b/c/fbc733078ba5e0b885acd2e22405e43a.png)