Kongruenzabbildungen/Parallelverschiebung/Dreiecke und Winkel/Seite 4: Unterschied zwischen den Versionen
Aus DMUW-Wiki
| (16 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
==Teilaufgabe d)== | ==Teilaufgabe d)== | ||
| − | + | <div style="border: 2px solid #FFFFFF; background-color:#ffffff; padding:7px;"> | |
| − | + | {| | |
| − | <ggb_applet height=" | + | | |
| − | + | <ggb_applet height="290" width="480" showResetIcon="true" filename="FußballfeldMMe).ggb" /> | |
| − | <br> | + | || |
| − | + | '''Ordne die Bilder, Winkel und Bezeichnungen den Oberbegriffen ''Wechsel-, Stufen-, Ergänzungs- und Nebenwinkel'' zu!'''<br> | |
| − | + | <div class="zuordnungs-quiz"> | |
| + | {| | ||
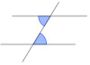
| + | | Wechselwinkel || Z-Winkel|| [[Bild:WwinkelMM1.jpg|90px]] || β und δ | ||
| + | |- | ||
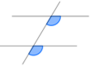
| + | | Stufenwinkel || F-Winkel|| [[Bild:SwinkelMM.png|90px]] || γ und ε | ||
| + | |- | ||
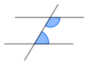
| + | | Ergänzungswinkel || [[Bild:EwinkelMM.png|90px]] || E-Winkel || β und θ | ||
| + | |- | ||
| + | | Nebenwinkel|| [[Bild:NwinkelMM.png|90px]] || ε und μ | ||
| + | |} | ||
| + | </div> | ||
| + | |} | ||
<quiz display="simple"> | <quiz display="simple"> | ||
| − | {'''Kreuze an, welche | + | {'''Kreuze an, welche Winkel sich zu 180° ergänzen und welche gleich groß sind!''' |
| − | + | | typ="[]" } | |
| + | | Nebenwinkel, | Stufenwinkel, | Ergänzungswinkel, | Wechselwinkel | ||
| − | + | + | -+-+ sind gleich groß |
| − | + | +-+- ergänzen sich zu 180° | |
| − | + | + | |
| − | + | ||
| − | - | + | |
| − | + | ||
| − | + | + | |
</quiz> | </quiz> | ||
| − | + | </div> | |
| − | '''2. | + | '''2. Jetzt fällt es dir bestimmt nicht mehr schwer, die fehlenden Winkel zu berechnen!'''<br/> |
| − | + | Tipp: Du musst die Winkel nicht in der Reihenfolge berechnen, in der sie unten stehen! | |
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
| − | + | α = '''68 (°)'''<br /> | |
| − | + | β = '''63 (°)'''<br /> | |
| − | + | γ = '''49 (°)'''<br /> | |
| − | + | θ = '''117 (°)'''<br /> | |
| − | </ | + | λ = '''63 (°)'''<br /> |
| − | + | μ = '''131 (°)'''<br /> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | ''' | + | |
| − | ''' | + | |
| − | < | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
</div> | </div> | ||
| − | '''→[[Kongruenzabbildungen/Parallelverschiebung/Dreiecke_und_Winkel/Seite 5| | + | '''<big>→[[Kongruenzabbildungen/Parallelverschiebung/Dreiecke_und_Winkel/Seite 5|Das war ganz schön viel. Zum Abschluss darfst du noch ein Memory lösen!]]</big>''' |
Aktuelle Version vom 13. Januar 2010, 16:33 Uhr
Teilaufgabe d)
|
|
Ordne die Bilder, Winkel und Bezeichnungen den Oberbegriffen Wechsel-, Stufen-, Ergänzungs- und Nebenwinkel zu! |
2. Jetzt fällt es dir bestimmt nicht mehr schwer, die fehlenden Winkel zu berechnen!
Tipp: Du musst die Winkel nicht in der Reihenfolge berechnen, in der sie unten stehen!
α = 68 (°)
β = 63 (°)
γ = 49 (°)
θ = 117 (°)
λ = 63 (°)
μ = 131 (°)
→Das war ganz schön viel. Zum Abschluss darfst du noch ein Memory lösen!