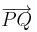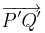Ähnlichkeitsabbildung/Zentrische Streckung mit Hilfe von Vektoren/Seite 4: Unterschied zwischen den Versionen
| (20 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | ==Teilaufgabe | + | ==Teilaufgabe c)== |
'''Du hast bereits gelernt, dass die zentrische Streckung auch mit Hilfe von Vektoren durchgeführt werden kann.'''<br/> | '''Du hast bereits gelernt, dass die zentrische Streckung auch mit Hilfe von Vektoren durchgeführt werden kann.'''<br/> | ||
'''Im Applet sind jetzt die Dreiecksseiten durch Pfeile dargestellt.''' | '''Im Applet sind jetzt die Dreiecksseiten durch Pfeile dargestellt.''' | ||
| − | <ggb_applet height="340" width="645" showResetIcon="true" filename="Dreieck_d)MM.ggb" /> | + | <div style="border: 2px solid #FFFFFF; background-color:#ffffff; padding:7px;"> |
| − | + | {|<br> | |
| − | + | |<ggb_applet height="340" width="645" showResetIcon="true" filename="Dreieck_d)MM.ggb" />|| | |
| − | '''1. Bearbeite | + | '''1. Bearbeite den Lückentext indem du die richtigen Symbole und Wörter in die Lücken ziehst.''' |
| − | + | ||
| − | + | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
| − | Durch eine zentrische Streckung mit dem '''Streckungsfaktor k''' wird der '''<span style="color:#EE6363">Urpfeil</span>''' <span style="color:#EE6363">< | + | Durch eine zentrische Streckung mit dem '''Streckungsfaktor k''' wird der '''<span style="color:#EE6363">Urpfeil</span>''' <span style="color:#EE6363"><math>\overrightarrow {PQ}</math></span> auf den '''<span style="color:#436EEE">Bildpfeil</span>''' <span style="color:#436EEE"><math>\overrightarrow {P'Q'}</math></span> abgebildet. Die Koordinaten des Bildpfeils erhält man durch folgende Rechnung:<br/> |
| + | '''<span style="color:#436EEE"><math>\overrightarrow {P'Q'}</math></span>''' = k <math>\cdot </math> '''<span style="color:#EE6363"><math>\overrightarrow {PQ}</math></span>'''. | ||
| + | </div> | ||
| + | |} | ||
</div> | </div> | ||
| Zeile 21: | Zeile 22: | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
| − | + | {| | |
| − | <span style="color:#EE6363">AB</span> | + | |- |
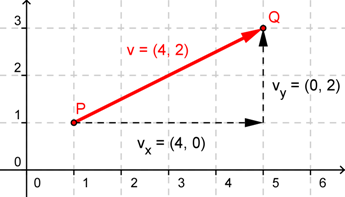
| − | <span style="color:#EE6363">BC</span> | + | | <span style="color:#EE6363"><math>\overrightarrow {AB}</math></span> = [[Bild:klammerMM.gif]] || |
| − | <span style="color:#EE6363">CA</span> | + | {| |
| + | |- | ||
| + | | '''4 (x-Koordinate des Pfeils)''' | ||
| + | |- | ||
| + | | '''1 (y-Koordinate des Pfeils)''' | ||
| + | |} | ||
| + | || [[Bild:klammer2MM.gif]] | ||
| + | |} | ||
| + | {| | ||
| + | |- | ||
| + | | <span style="color:#EE6363"><math>\overrightarrow {BC}</math></span> = [[Bild:klammerMM.gif]] || | ||
| + | {| | ||
| + | |- | ||
| + | | '''-2 (x-Koordinate des Pfeils)''' | ||
| + | |- | ||
| + | | '''2 (y-Koordinate des Pfeils)''' | ||
| + | |} | ||
| + | || [[Bild:klammer2MM.gif]] | ||
| + | |} | ||
| + | {| | ||
| + | |- | ||
| + | | <span style="color:#EE6363"><math>\overrightarrow {CA}</math></span> = [[Bild:klammerMM.gif]] || | ||
| + | {| | ||
| + | |- | ||
| + | | '''-2 (x-Koordinate des Pfeils)''' | ||
| + | |- | ||
| + | | '''-3 (y-Koordinate des Pfeils)''' | ||
| + | |} | ||
| + | || [[Bild:klammer2MM.gif]] | ||
| + | |} | ||
</div> | </div> | ||
| + | |||
| + | | ||
'''3. Wie lauten die Koordinaten der <span style="color:#436EEE">Bildpfeile</span> für k = 0,5?''' | '''3. Wie lauten die Koordinaten der <span style="color:#436EEE">Bildpfeile</span> für k = 0,5?''' | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
| − | |||
| − | |||
| − | <span style="color:#436EEE">A'B'</span> | + | {| |
| − | <span style="color:#436EEE">B'C'</span> | + | |- |
| − | <span style="color:#436EEE">C'A'</span> | + | | <span style="color:#436EEE"><math>\overrightarrow {A'B'}</math></span> = [[Bild:klammerMM.gif]] || |
| + | {| | ||
| + | |- | ||
| + | | '''2 (x-Koordinate des Pfeils)''' | ||
| + | |- | ||
| + | | '''0,5 (y-Koordinate des Pfeils)''' | ||
| + | |} | ||
| + | || [[Bild:klammer2MM.gif]] | ||
| + | |} | ||
| + | {| | ||
| + | |- | ||
| + | | <span style="color:#436EEE"><math>\overrightarrow {B'C'}</math></span> = [[Bild:klammerMM.gif]] || | ||
| + | {| | ||
| + | |- | ||
| + | | '''-1 (x-Koordinate des Pfeils)''' | ||
| + | |- | ||
| + | | '''1 (y-Koordinate des Pfeils)''' | ||
| + | |} | ||
| + | || [[Bild:klammer2MM.gif]] | ||
| + | |} | ||
| + | {| | ||
| + | |- | ||
| + | | <span style="color:#436EEE"><math>\overrightarrow {C'A'}</math></span> = [[Bild:klammerMM.gif]] || | ||
| + | {| | ||
| + | |- | ||
| + | | '''-1 (x-Koordinate des Pfeils)''' | ||
| + | |- | ||
| + | | '''-1,5 (y-Koordinate des Pfeils)''' | ||
| + | |} | ||
| + | || [[Bild:klammer2MM.gif]] | ||
| + | |} | ||
</div> | </div> | ||
| − | '''4.''' | + | |
| + | |||
| + | '''4. Ein anderes Dreieck wird nun mit dem Streckungsfaktor k = '''-''' 4 zentrisch gestreckt. | ||
| + | |||
| + | Für die Urpfeile des Dreiecks gilt: <math>\overrightarrow {AB}</math> = <math>\ {-3\choose 2} </math>, <math>\overrightarrow {BC}</math> = <math>\ {1\choose 3} </math>. | ||
| + | |||
| + | Berechne die Koordinaten der zugehörigen Bildpfeile! | ||
| + | <div class="lueckentext-quiz"> | ||
| + | {| | ||
| + | |- | ||
| + | | <span style="color:#436EEE"><math>\overrightarrow {A'B'}</math></span> = [[Bild:klammerMM.gif]] || | ||
| + | {| | ||
| + | |- | ||
| + | | '''12 (x-Koordinate des Pfeils)''' | ||
| + | |- | ||
| + | | '''-8 (y-Koordinate des Pfeils)''' | ||
| + | |} | ||
| + | || [[Bild:klammer2MM.gif]] | ||
| + | |} | ||
| + | {| | ||
| + | |- | ||
| + | | <span style="color:#436EEE"><math>\overrightarrow {B'C'}</math></span> = [[Bild:klammerMM.gif]] || | ||
| + | {| | ||
| + | |- | ||
| + | | '''-4 (x-Koordinate des Pfeils)''' | ||
| + | |- | ||
| + | | '''-12 (y-Koordinate des Pfeils)''' | ||
| + | |} | ||
| + | || [[Bild:klammer2MM.gif]] | ||
| + | |} | ||
| + | </div> | ||
| + | |||
| + | Der Bildpfeil zum Pfeil <math>\overrightarrow {CA}</math> hat nach der Streckung die Koordinaten <math>\overrightarrow {C'A'}=</math> <math>\ {8 \choose 4} </math>. Welche Koordinaten hatte der Urpfeil <math>\overrightarrow {CA}</math>?''' | ||
| + | |||
| + | <div class="lueckentext-quiz"> | ||
| + | {| | ||
| + | |- | ||
| + | | <span style="color:#436EEE"><math>\overrightarrow {CA}</math></span> = [[Bild:klammerMM.gif]] || | ||
| + | {| | ||
| + | |- | ||
| + | | '''-2 (x-Koordinate des Pfeils)''' | ||
| + | |- | ||
| + | | '''-1 (y-Koordinate des Pfeils)''' | ||
| + | |} | ||
| + | || [[Bild:klammer2MM.gif]] | ||
| + | |} | ||
| + | </div> | ||
| + | |||
| + | '''Das war gar nicht so leicht. Aber du hast das ganz toll gemacht! | ||
| − | '''→[[Ähnlichkeitsabbildung/Zentrische Streckung mit Hilfe von Vektoren/Seite 5| | + | '''<big>→[[Ähnlichkeitsabbildung/Zentrische Streckung mit Hilfe von Vektoren/Seite 5|Schnell weiter zu Teilaufgabe d)!]]</big>''' |
Aktuelle Version vom 13. Januar 2010, 17:17 Uhr
Teilaufgabe c)
Du hast bereits gelernt, dass die zentrische Streckung auch mit Hilfe von Vektoren durchgeführt werden kann.
Im Applet sind jetzt die Dreiecksseiten durch Pfeile dargestellt.
|
1. Bearbeite den Lückentext indem du die richtigen Symbole und Wörter in die Lücken ziehst. Durch eine zentrische Streckung mit dem Streckungsfaktor k wird der Urpfeil |
2. Gib die Koordinaten der Urpfeile an!
Weißt du nicht mehr genau, wie man Koordinaten von Pfeilen berechnet, dann lass dir folgenden Tipp anzeigen!
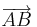 = = |
|
|
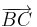 = = |
|
|
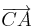 = = |
|
|
3. Wie lauten die Koordinaten der Bildpfeile für k = 0,5?
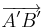 = = |
|
|
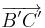 = = |
|
|
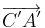 = = |
|
|
4. Ein anderes Dreieck wird nun mit dem Streckungsfaktor k = - 4 zentrisch gestreckt.
Für die Urpfeile des Dreiecks gilt: 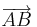 =
= 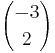 ,
, 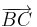 =
= 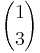 .
.
Berechne die Koordinaten der zugehörigen Bildpfeile!
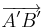 = = |
|
|
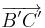 = = |
|
|
Der Bildpfeil zum Pfeil 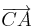 hat nach der Streckung die Koordinaten
hat nach der Streckung die Koordinaten 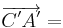
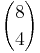 . Welche Koordinaten hatte der Urpfeil
. Welche Koordinaten hatte der Urpfeil 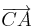 ?
?
Das war gar nicht so leicht. Aber du hast das ganz toll gemacht!