Lernpfad2: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
 
(54 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 3: Zeile 3:
  
 
'''In diesem Lernpfad wird die Addition von Brüchen mit jeweils einer kurzen Einführung und Übungsaufgaben wiederholt.'''<br />
 
'''In diesem Lernpfad wird die Addition von Brüchen mit jeweils einer kurzen Einführung und Übungsaufgaben wiederholt.'''<br />
−
*'''Addition von gleichnahmigen Brüchen'''
+
*'''Addition von gleichnamigen Brüchen'''
−
*'''Addition von ungleichnahmigen Brüchen mit Nenner als Vielfache'''
+
*'''Addition von ungleichnamigen Brüchen mit Nenner als Vielfache'''
 
}}
 
}}
  
 +
__NOCACHE__
 +
 +
 +
'''Zeitbedarf:''' 35 Min.
  
−
*'''Zeitbedarf:''' 35 Min.
 
−
*'''Material:''' Laufzettel und einen Stift
 
  
  
Zeile 17: Zeile 19:
  
  
−
=1.Station: Addition von gleichnahmigen Brüchen=
+
=1. Addition von gleichnamigen Brüchen=
  
  
Zeile 40: Zeile 42:
 
<div class="multiplechoice-quiz">
 
<div class="multiplechoice-quiz">
  
−
Welche Lösung<u>en</u> sind richtig? (<math> \frac{6}{12} </math>) (!<math> \frac{5}{12} </math>) (<math> \frac{1}{2} </math>)  
+
'''Welchen Bruchteil von Stunden ist Svenja insgesamt unterwegs, wenn sie <math> \frac{1}{12} </math>h zu Fuß zur Bushaltestelle läuft und <math> \frac{5}{12} </math>h mit dem Bus fährt? ''' (<math> \frac{6}{12} </math>h) (!<math> \frac{6}{24} </math>h) (!<math> \frac{5}{12} </math>h)  
 +
</div>
 +
&nbsp;
 
</div>
 
</div>
  
  
 +
<div style="border: 2px solid #008B45; background-color:#ffffff; padding:7px;">
  
 +
'''Markiere nun die einzelnen Bruchteile der gegebenen Brüche in den Zeichnungen und bestimme das Ergebnis!'''
  
 +
'''Um die Bruchteile einzeichnen zu können, musst du mit der linken Maustaste auf das Quadrat klicken. '''
  
 +
'''Prüfe deine Ergebnisse!'''
  
  
 +
'''a)'''&nbsp;&nbsp;
  
−
Berechne nun die folgenden Aufgaben mit Hilfe der bildlichen Veranschaulichung der oben stehen Uhren und schreibe die Lösung auf deinen Laufzettel.
+
&nbsp;&nbsp; <ggb_applet height="150" width="600" showResetIcon="true" filename="Ann-Kathrin_Hey_Aufgabe2a.ggb" />
  
−
(kürze die Lösung soweit wie möglich)
+
<div class="lueckentext-quiz">
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;<math>\frac{3}{8}</math>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;+&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;<math>\frac{2}{8}</math>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; = &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; ''' 5 (Zähler)''' /'''8 (Nenner)'''
 +
</div>
  
  
  
−
a) <math> \frac{2}{12} </math> + <math> \frac{9}{12} </math>  
+
'''b)'''&nbsp;&nbsp;
−
b) <math> \frac{3}{12} </math> + <math> \frac{4}{12} </math>  
+
 
−
c) <math> \frac{9}{12} </math> + <math> \frac{10}{12} </math>
+
&nbsp;&nbsp;<ggb_applet height="200" width="600" showResetIcon="true" filename="Ann-Kathrin_Hey_Aufgabe2c.ggb" />
 +
 
 +
<div class="lueckentext-quiz">
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;<math>\frac{2}{5}</math>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;+&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;<math>\frac{2}{5}</math>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; = &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; ''' 4 (Zähler)''' /'''5 (Nenner)'''
 +
 
 +
</div>
 +
&nbsp;
 
</div>
 
</div>
  
  
 +
<div style="border: 2px solid #008B45; background-color:#ffffff; padding:7px;">
 +
'''Schreibe nun das Ergebnis, der bildlich dargestellten Brüche, in die Platzhalter nebenan!'''
  
 +
'''Bist du damit fertig, klicke auf <span style="color:#ff0000">prüfen!</span>'''
  
−
An den Beispielen sind dir bestimmt Vorgehensweisen  aufgefallen wie Brüche addiert werden.
+
<div class="lueckentext-quiz">
  
−
Die wichtigsten Regeln, an die du denken musst, sind hier nun aufgelistet:
+
[[Bild:Ann-Kathrin_Hey_ikonisch_Aufgabe1c.png]] + [[Bild:Ann-Kathrin_Hey_ikonisch_Aufgabe1c2.png]]  =  '''7 (Zähler)''' /'''9 (Nenner)'''
 +
</div>
 +
{|
 +
|<div class="lueckentext-quiz">
 +
[[Bild:Ann-Kathrin_Hey_Messbecher2.png]] + [[Bild:Ann-Kathrin_Hey_Messbecher2.png]] 
 +
</div>
 +
||<div class="lueckentext-quiz">
 +
=  ''' 2(Zähler)'''/'''4(Nenner)''' <br>
 +
= ''' 1(Zähler)'''/'''2(Nenner)'''(gekürzte Lösung)
 +
</div>
 +
|}
  
  
 +
<div class="lueckentext-quiz">
 +
[[Bild:Ann-Kathrin_Hey_Schokolade1.png]] + [[Bild:Ann-Kathrin_Hey_Schokolade2.png]]  =  '''17 (Zähler)''' /'''18 (Nenner)'''
 +
</div>
  
−
<div style="border: 2px solid red; background-color:#ffffff; padding:7px;">
 
−
'''Addition gleichnamiger Brüche'''
 
  
−
** Gleichnamige Brüche werden addiert, indem man die '''Zähler addiert''' und der '''gemeinsame Nenner beibehalten''' wird.
+
<div class="lueckentext-quiz">
−
** Das Ergebnis kürzt man soweit wie möglich oder wandelt es in eine gemischte Zahl um.
+
[[Bild:Ann-Kathrin_Hey_Pizza1.png]] + [[Bild:Ann-Kathrin_Hey_Pizza4.png]]  =  '''3 (Zähler)''' /'''4 (Nenner)'''
 +
</div>
  
 +
&nbsp;
 
</div>
 
</div>
 +
  
  
 
<div style="border: 2px solid blue; background-color:#ffffff; padding:7px;">
 
<div style="border: 2px solid blue; background-color:#ffffff; padding:7px;">
−
Beispiel "Uhr" von oben: <math> \frac{1}{12} </math>h + <math> \frac{5}{12} </math> = <math> \frac{1 + 5}{12} </math>h = <math> \frac{6}{12} </math>h = <math> \frac{1}{2} </math>h &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;
+
Nachdem du nun einige Erfahrungen zur Addition von Brüchen gemacht hast, wird es dir leicht fallen das inhaltliche Verständnis der Additionsregel von Brüchen zu verstehen.
−
[[Bild:Ann-Kathrin_Hey_Uhr.png]]
+
 
 +
Beispiel: 2 '''''Neuntel''''' + 3 '''''Neuntel''''' = 5 '''''Neuntel'''''
 +
         
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;oder
 +
 
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;2 [[Bild:Ann-Kathrin_Hey_Himbeere1.png]] + 3 [[Bild:Ann-Kathrin_Hey_Himbeere1.png]]  = 5 [[Bild:Ann-Kathrin_Hey_Himbeere1.png]]
 +
 
 +
An diesem Beispiel kannst du erkennen, dass der Nenner sich nie ändert ('''''Neuntel''''' / [[Bild:Ann-Kathrin_Hey_Himbeere1.png]]). Nur die Zähler werden addiert und sagen etwas über die Anzahl der Einheiten aus.
 +
 
 
</div>
 
</div>
  
  
−
<div style="border: 2px solid #00c5cd; background-color:#ffffff; padding:7px;">
 
−
Damit du sicher gehen kannst, dass du die Addition von gleichnahmigen Brüchen verstanden hast, versuche nun das Memory zu lösen.
 
  
−
'''Beachte: Es gehören immer drei Memoryteile zusammen (Additionsaufgabe, Bruch als Ergebnis und ein Bild als Ergebnis)'''
 
  
−
<div class="memo-quiz">
+
 
−
{|
+
&nbsp;&nbsp;[[Bild:Ann-Kathrin_Hey_Sprechblase_Himbeere.png]]&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;[[Bild:Ann-Kathrin_Hey_Sprechblase_Fragezeichen.png]]
−
|-
+
 
−
| [[Bild:Ann-Kathrin_Hey_Memorie1.png]] || <math> \frac{1}{8} </math> + <math> \frac{5}{8} </math> ||  <math> \frac{3}{4} </math>
+
 
−
|-
+
 
−
| [[Bild:Ann-Kathrin_Hey_Memorie2.png]] ||  <math> \frac{4}{12} </math> + <math> \frac{3}{12} </math> ||  <math> \frac{7}{12} </math>
+
 
−
|-
+
 
−
| [[Bild:Ann-Kathrin_Hey_Memorie3.png]] || <math> \frac{4}{24} </math> + <math> \frac{7}{24} </math> ||  <math> \frac{11}{24} </math>
+
Brüche, die '''denselben Nenner''' haben, nennt man ''''<span style="color:#ff0000">gleichnamige Brüche</span>''''.
−
|-
+
 
−
| [[Bild:Ann-Kathrin_Hey_Memorie4.png]] ||  <math> \frac{1}{8} </math> + <math> \frac{2}{8} </math> ||  <math> \frac{3}{8} </math>
+
Im Folgenden ist nun alles zusammengefasst, was du über die Addition von gleichnamigen Brüchen wissen musst.
 +
 
 +
'''Lese es dir konzentriert durch!'''
 +
 
 +
 
 +
{|
 +
|[[Bild:Ann-Kathrin_Hey_Animation_Ausrufezeichen.png]]||
 +
 
 +
<div style="border: 2px solid red; background-color:#ffffff; padding:7px;">
 +
=== '''Addition gleichnamiger Brüche''' ===
 +
 
 +
'''* Gleichnamige Brüche werden addiert, indem man die <span style="color:#ff0000">Zähler addiert</span> und der <span style="color:#ff0000">gemeinsame Nenner beibehalten</span> wird.'''
 +
 
 +
'''* Das Ergebnis kürzt man soweit wie möglich oder wandelt es in eine gemischte Zahl um.'''
 +
</div>
 
|}
 
|}
  
  
 +
{|
 +
|&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;'''Allgemein:  &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;||
 +
<div style="border: 2px solid red; background-color:#ffffff; padding:7px;">  <math> \frac{a}{b} </math> + <math> \frac{c}{b} </math> = <math> \frac{a + c}{b} </math>'''
 
</div>
 
</div>
 +
|}
 +
 +
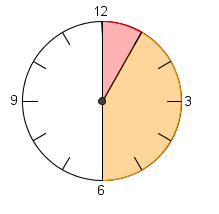
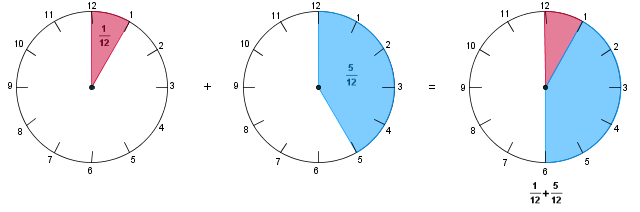
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;'''Beispiel von oben''' "Uhr": &nbsp;&nbsp; <math> \frac{1}{12} </math>h + <math> \frac{5}{12} </math> = <math> \frac{1 + 5}{12} </math>h = <math> \frac{6}{12} </math>h = <math> \frac{1}{2} </math>h &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;
 +
[[Bild:Ann-Kathrin_Hey_Uhr.png]]
 +
 +
  
  
  
−
'''→[[Repräsentationsformen: ikonisch/Seite 2|Hier geht`s zur 2. Seite]]'''
+
'''<big>→[[Lernpfade/Addition von Brüchen/Lernpfad2 Seite 2|Hier geht`s zur 2. Seite]]</big>'''

Aktuelle Version vom 21. März 2019, 18:44 Uhr


Mathematik-digital Pfeil-3d.png
Lernpfad

Addition von Brüchen

In diesem Lernpfad wird die Addition von Brüchen mit jeweils einer kurzen Einführung und Übungsaufgaben wiederholt.

  • Addition von gleichnamigen Brüchen
  • Addition von ungleichnamigen Brüchen mit Nenner als Vielfache



Zeitbedarf: 35 Min.



Ann-Kathrin Hey Animation Uhr1.PNG


1. Addition von gleichnamigen Brüchen

Einführung:
Svenja geht jeden Morgen um 7.00 Uhr aus dem Haus, um pünklich in der Schule zu sein. Sie muss 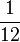\frac{1}{12} h zu Fuß zur Bushaltestelle laufen. Dort steigt sie in den Schulbus ein, der 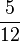\frac{5}{12} h bis zur Schule braucht.

Wie lange ist sie insgesamt unterwegs?


Die Veranschaulichung der Additionsaufgabe durch die dargestellten Uhren soll dir beim Lösen der Aufgabe helfen.


Ann-Kathrin Hey ikonisch Einführung.png


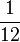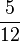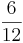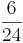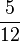Welchen Bruchteil von Stunden ist Svenja insgesamt unterwegs, wenn sie \frac{1}{12} h zu Fuß zur Bushaltestelle läuft und \frac{5}{12} h mit dem Bus fährt? ( \frac{6}{12} h) (! \frac{6}{24} h) (! \frac{5}{12} h)

 


Markiere nun die einzelnen Bruchteile der gegebenen Brüche in den Zeichnungen und bestimme das Ergebnis!

Um die Bruchteile einzeichnen zu können, musst du mit der linken Maustaste auf das Quadrat klicken.

Prüfe deine Ergebnisse!


a)  

  

                        \frac{3}{8}                 +                         \frac{2}{8}                  =            5 (Zähler) /8 (Nenner)


b)  

  

                        \frac{2}{5}                         +                               \frac{2}{5}             =                 4 (Zähler) /5 (Nenner)

 


Schreibe nun das Ergebnis, der bildlich dargestellten Brüche, in die Platzhalter nebenan!

Bist du damit fertig, klicke auf prüfen!

Ann-Kathrin Hey ikonisch Aufgabe1c.png + Ann-Kathrin Hey ikonisch Aufgabe1c2.png = 7 (Zähler) /9 (Nenner)

Ann-Kathrin Hey Messbecher2.png + Ann-Kathrin Hey Messbecher2.png

= 2(Zähler)/4(Nenner)
= 1(Zähler)/2(Nenner)(gekürzte Lösung)


Ann-Kathrin Hey Schokolade1.png + Ann-Kathrin Hey Schokolade2.png = 17 (Zähler) /18 (Nenner)


Ann-Kathrin Hey Pizza1.png + Ann-Kathrin Hey Pizza4.png = 3 (Zähler) /4 (Nenner)

 


Nachdem du nun einige Erfahrungen zur Addition von Brüchen gemacht hast, wird es dir leicht fallen das inhaltliche Verständnis der Additionsregel von Brüchen zu verstehen.

Beispiel: 2 Neuntel + 3 Neuntel = 5 Neuntel

             oder

             2 Ann-Kathrin Hey Himbeere1.png + 3 Ann-Kathrin Hey Himbeere1.png = 5 Ann-Kathrin Hey Himbeere1.png

An diesem Beispiel kannst du erkennen, dass der Nenner sich nie ändert (Neuntel / Ann-Kathrin Hey Himbeere1.png). Nur die Zähler werden addiert und sagen etwas über die Anzahl der Einheiten aus.



  Ann-Kathrin Hey Sprechblase Himbeere.png      Ann-Kathrin Hey Sprechblase Fragezeichen.png



Brüche, die denselben Nenner haben, nennt man 'gleichnamige Brüche'.

Im Folgenden ist nun alles zusammengefasst, was du über die Addition von gleichnamigen Brüchen wissen musst.

Lese es dir konzentriert durch!


Ann-Kathrin Hey Animation Ausrufezeichen.png

Addition gleichnamiger Brüche

* Gleichnamige Brüche werden addiert, indem man die Zähler addiert und der gemeinsame Nenner beibehalten wird.

* Das Ergebnis kürzt man soweit wie möglich oder wandelt es in eine gemischte Zahl um.


                        Allgemein:       
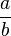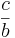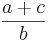
\frac{a}{b} + \frac{c}{b} = \frac{a + c}{b}

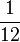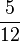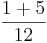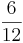                        Beispiel von oben "Uhr":    \frac{1}{12} h + \frac{5}{12} = \frac{1 + 5}{12} h = \frac{6}{12} h = \frac{1}{2} h        Ann-Kathrin Hey Uhr.png



→Hier geht`s zur 2. Seite

Von „http://dmuw.zum.de/index.php?title=Lernpfade/Addition_von_Brüchen/Lernpfad2&oldid=32168“