Übungsaufgaben zum Satz des Thales: Unterschied zwischen den Versionen
| Zeile 5: | Zeile 5: | ||
<br> | <br> | ||
<div style="border: 2px solid blue; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid blue; background-color:#ffffff; padding:7px;"> | ||
| + | [[Bild: ThalesClownaufgabenvorlage_NicoStahl.jpg|thumb|center|500px|Ich bin der Thales-Clown]] <br> | ||
| + | <br> | ||
| + | : '''Erinnerst du dich noch an die Beispiele im letzten Lernpfad?''' | ||
| + | <br> | ||
| + | <br> | ||
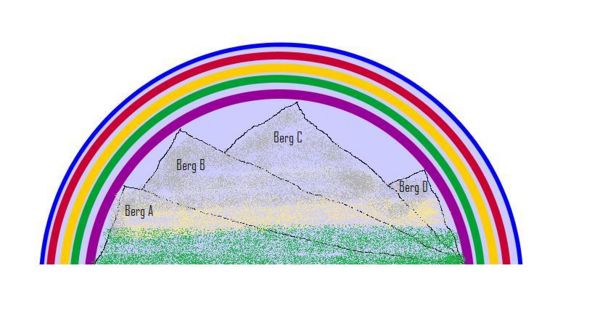
'''Hier siehst du einen schönen Regenbogen mitten in einer Berglandschaft auf dem Planet Phantasia.''' | '''Hier siehst du einen schönen Regenbogen mitten in einer Berglandschaft auf dem Planet Phantasia.''' | ||
[[Bild: regenbogen_nico.jpg|thumb|left|Berglandschaft mit Regenbogen|600px]] | [[Bild: regenbogen_nico.jpg|thumb|left|Berglandschaft mit Regenbogen|600px]] | ||
Version vom 22. Juni 2009, 17:30 Uhr
|
Lernpfad
|
- Erinnerst du dich noch an die Beispiele im letzten Lernpfad?
Hier siehst du einen schönen Regenbogen mitten in einer Berglandschaft auf dem Planet Phantasia.
Welcher Gipfel dieser Berglandschaft ist am spitzesten?
Frage a): Hast du eine Idee, wie groß der Winkel am Gipfel von Berg A sein könnte?
Antwort a): Der Berg A hat am Gipfel ein Winkelmaß von: 90°
Frage b): Haben die Winkel der Berge A,B,C,D, die den Regenbogen berühren eine Gemeinsamkeit?
Antwort b): Alle Winkel, die den Regenbogen berühren sind gleich groß.
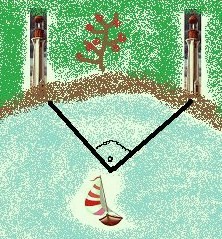
Ein Matrose und sein Kapitän segeln zusammen am Meeresufer entlang und entdecken zwei Leuchttürme unter einem Winkel von 90°.
- Überlegungen:
- Welche Position könnte denn das Segelschiff haben?
- Stehen die beiden Leuchttürme zueinander in Beziehung?
- Könnte es sich um eine geometrische Figur handeln, wenn man Objekte miteinander verbindet?
- Was bedeutet die Angabe: "unter einem Winkel von 90°" Was kannst du daraus schließen?
Auf gehts - löse den Lückentext:
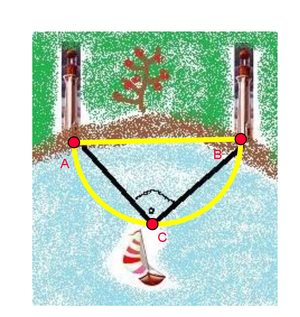
Zwei Standorte auf dem Festland werden mit A und B bezeichnet. In der Zeichnung sind das die Leuchttürme .
Das Objekt im Meer, also das Segelschiff wird mit dem Buchstaben C versehen.
Nun verbinden wir die Punkte A,B und C miteinander und erhalten ein rechtwinkliges Dreieck.
Der Winkel an der Spitze C beträgt 90°.
Der Matrose und sein Kapitän segeln mit dem Schiff vom linken zum rechten Leuchtturm genau so, dass der Winkel bei C stets ein Maß von 90° hat.
Dies lässt vermuten, dass die gefahrene Route einen Halbkreis ergibt.
Den Mittelpunkt dieses Halbkreises bildet die Strecke AB .
Anhand dieser Zeichnung kannst du den Zusammenhang erkennen, den du im Lückentext erarbeiten solltest.
Frage a): Wenn das Schiff zum Leuchtturm B fährt, unter welchem Winkel blicken der Matrose und der Kapitän aufs Festland?
Antwort a): Die beiden Seeleute betrachten es von einem 90° Winkel aus.
Frage b): Wenn aber das Schiff zum Leuchtturm A fährt, unter welchem Winkel blicken dann die Schiffsleute aufs Festland ?
Antwort b): Dann betrachten es die Seemänner von einem 90° Winkel aus.
| Daraus können wir schließen, dass der Winkel bei C immer rechtwinklig ist, |
Kategorie: -leicht-
|
1. Arbeitsauftrag:
|
Kategorie: -mittelschwierig-
|
2. Arbeitsauftrag:
|
Kategorie: -schwierig-
|
3. Arbeitsauftrag:
|
Die folgende Aufgabe ist zum Knüffeln für Profis gedacht!!!
Die rutschende Leiter:
| Ziehe an dem grünen Punkt B | Anmerkungen und Arbeitsauftrag | |
|---|---|---|
| Was fällt dir auf, wenn du am grünen Punkt B ziehst? |
Der Satz des Thales findet Anwendung beim Lösen dieses Problems.
Weitere Informationen erhaltet ihr auch auf dieser Homepage: |
|
Entstanden unter Mitwirkung von:
|