|
|
| Zeile 195: |
Zeile 195: |
| | </div> | | </div> |
| | <br> | | <br> |
| − | <br>
| |
| − | <br>
| |
| − | <br>
| |
| − | <div style="border: 2px solid blue; background-color:#ffffff; padding:7px;"> <br>
| |
| − |
| |
| − | ===Viel Spaß beim Multiple-Choice!===
| |
| − | <br>
| |
| − | '''''Beziehe dich bei der Beantwortung der Aufgaben auf die nebenstehende Zeichnungen!!!'''''
| |
| − | <br>
| |
| − | {|
| |
| − | | <quiz display="simple">
| |
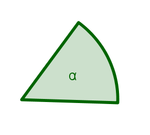
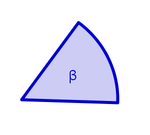
| − | { '''Welche Aussagen über die Winkel α und β sind wahr?'''}
| |
| − |
| |
| − | - Die Summe aus den Winkeln α + β ergeben zusammen immer 60°.
| |
| − | + Die Summe der beiden Winkel α + β ist immer gleich.
| |
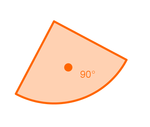
| − | + Das Maß des Winkels γ an der Spitze C berechnet sich aus der Summe der Winkel α + β.
| |
| − | - Der Winkel β kann nie doppelt so groß sein wie der Winkel α.
| |
| − | - Der Winkel α misst immer 90°.
| |
| − | - Der Winkel β misst immer 90°.
| |
| − | + Falls gilt: α = 45°, so folgt: α = β.
| |
| − | - Die beiden Winkel α und β sind nie maßgleich.
| |
| − |
| |
| − | { '''Welche Aussagen über den Winkel γ sind wahr?'''}
| |
| − |
| |
| − | + Der Winkel γ misst immer 90°.
| |
| − | - Der Winkel γ misst nie 90°.
| |
| − | - Für den Winkel γ gilt: γ < 90°.
| |
| − | - Für den Winkel γ gilt: γ > 90°.
| |
| − | + Für den Winekl γ gilt: γ = 90°.
| |
| − | <br>
| |
| − | </quiz> || <ggb_applet height="350" width="610" showResetIcon="true" filename="KreuzwortThales_nicostahl.ggb" /> <br> <br> <ggb_applet height="350" width="610" showResetIcon="true" filename="ThalesKreuz_Nico.Stahl.ggb" />
| |
| − | |}
| |
| − | </div>
| |
| | <br> | | <br> |
| | <br> | | <br> |
Version vom 23. Juni 2009, 16:33 Uhr
- Nach dem griechischen Philosophen und Mathematiker Thales von Milet (um 600 v. Chr.) wird ein wichtiger gemeotrischer Satz bezeichnet.
Betrachte aufmerksam die dynamische Animation!
|
|
Auf gehts - Löse das Quiz!
Beziehe dich dabei auf die nebenstehende Animation.
Wenn die Strecke AB den Mittelpunkt M des Kreises schneidet, dann erscheint im Bild das Wort Thales.
Weiterhin gilt dann auch, dass der Winkel an der Spitze C (grün markiert) rechtwinklig ist.
Wenn das Dreieck ABC bei C ein Maß von 90° hat, so bezeichnet man die Strecke AB als Hypotenuse.
Die beiden Strecken AC und BC nennt man Katheten.
|
|
|
Betrachte aufmerksam die dynamische Animation!
Versuche den Lückentext mithilfe der dynamischen Zeichnung zu lösen.
Wenn das Dreieck ABC bei dem Eckpunkt C rechtwinklig ist, dann liegt C auf dem Halbkreis über dem Durchmesser AB.
Wenn der Punkt C auf dem Halbkreis über AB liegt, dann ist das Dreieck ABC rechtwinklig bei C.
|
|
In der Mathematik kommt es häufig vor, dass Satz und Kehrsatz richtig sind.
Anstelle von zwei Sätzen in Wenn-Dann-Form, wird die Formulierung "...genau dann, wenn..." verwendet,
sowohl um die Sätze zusammenzufassen als auch um die Korrektheit der Aussage zu artikulieren.
|
Das Dreieck ABC hat genau dann bei C einen rechten Winkel, wenn die Ecke C auf dem Halbkreis über der Strecke AB liegt.
|
|
Auf gehts - löse den Lückentext:
Fülle die Lücken, indem du die passenden Begriffe zu den Feldern ziehst (mit der linken Maustaste zur Lücke ziehen und fallenlassen).
Wir wollen diesen Sachverhalt nun mathematisch untersuchen und dazu gehen wir davon aus,
dass das in der Zeichnung ersichtliche Dreieck einen rechten Winkel bei C aufzeigt.
Also sind die Punkte A, B und C gleich weit von M entfernt,
liegen somit auf dem Kreis um M,
der zugleich Mittelpunkt von der Strecke AB ist.
Das heißt, wenn das Dreieck ABC bei der Ecke C rechtwinklig ist,
dann liegt C auf dem Halbkreis über der Strecke AB.
Die Strecke AB ist zudem auch der Durchmesser des THALES-KREISES .
|
|
!!!Ziehe am roten Punkt C. Beobachte dabei den Wert für den Winkel γ!!!
- 1.Frage: Welchen Wert nimmt der Winkel γ an, wenn sich der rote Punkt C innerhalb des gelben Halbkreises befindet?
- 1.Antwort: Der Winkel γ ist größer als 90°. Es gilt: γ > 90°
- 2.Frage: Welchen Wert nimmt der Winkel γ an, wenn sich der rote Punkt C außerhalb des gelben Halbkreises befindet? (Jedoch innerhalb der blauen Linien?)
- 2.Antwort: Der Winkel γ ist kleiner als 90°. Es gilt: γ < 90°
- 3.Frage: Welchen Wert nimmt der Winkel γ an, wenn sich der rote Punkt C genau auf dem Halbkreis befindet?
- 3.Antwort: Der Winkel γ beträgt dann genau 90°. Es gilt: γ = 90°
- 4.Frage: Welchen Wert nimmt der Winkel γ an, wenn du das Kästchen "Punkt fixieren" anklickst?
- 4.Antwort: Der Winkel γ beträgt dann genau 90°. Es gilt: γ = 90°
Erklärung: Es gilt: γ = 90°, weil der rote Punkt C genau auf dem Halbreis über der Strecke [AB] liegt.
|
|
Der Satz des Thales:
Jedes Dreieck ∆ABC, dessen Grundseite AB dem Durchmesser eines Halbkreises entspricht und dessen Ecke C auf dem Kreisbogen liegt,
ist rechtwinklig. Den Halbkreis mit dem eingeschlossenen Dreieck bezeichnet man kurz als „Thales-Kreis“.
|
- Eigentlich, müsstest du jetzt doch alles verstanden haben, oder?
- Die nachstehenden Aufgaben kannst du in Absprache mit deinem Lehrer oder deiner Lehrerin bearbeiten!
Aufgabe 
Arbeitsauftrag:
- Konstruiere in dein Übungsheft einen Thales-Kreis.
- Schreibe die besonderen Eigenschaften eines Thales-Kreis in dein Heft.
- Füge sonstige Besonderheiten hinzu, die dir während des Bearbeitens des Lernpfades aufgefallen sind.
- Diskutiere in deiner Klassengemeinschaft über diesen Lernpfad
|