Eigenschaften: Unterschied zwischen den Versionen
Aus DMUW-Wiki
(Inhaltsverzeichnis beigefügt) |
(Nummerierung geändert) |
||
| Zeile 19: | Zeile 19: | ||
{{Merksatz|MERK= | {{Merksatz|MERK= | ||
| − | + | * Die Definitionsmenge aller Exponentialfunktionen ist R. | |
| − | + | * Es treten nur positive Funktionswerte auf. | |
| − | + | * Alle Exponentialfunktionen der Form f(x) = ax gehen durch den Punkt (0/1). | |
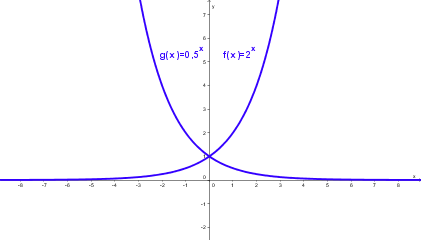
| − | + | * Die Graphen von f(x) = ax und liegen symmetrisch bezüglich der y-Achse. | |
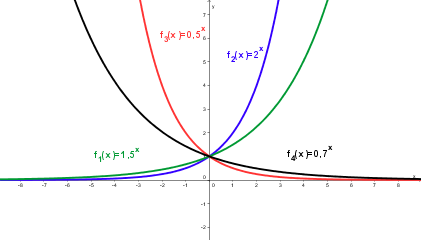
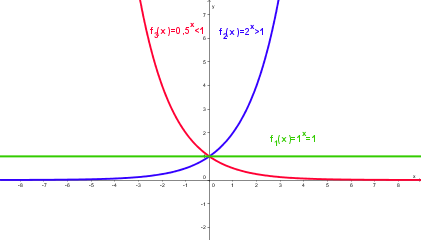
| − | + | * Für 0 < a < 1 ist die Exponentialfunktion monoton fallend, für a = 1 ist die Funktion konstant, für a > 1 ist sie monoton steigend. | |
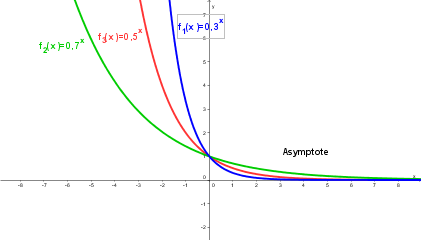
| − | + | * für 0 < a < 1 ist die positive x-Achse Asymptote. | |
| − | + | * Für a > 1 ist die negative x-Achse Asymptote.}} | |
Version vom 16. Januar 2010, 18:27 Uhr
Übersicht - Einleitung - Zinseszins - Untersuchung der Exponentialfunktion - Eigenschaften der Exponentialfunktion - Umkehrfunktion - Übungen und Lösung des Arbeitsblattes - Rechnerische Beziehung zwischen der Exponentialfunktion und der Logarithmusfunktion
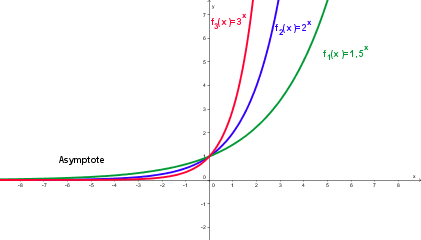
Eigenschaften der Exponentialfunktion
| Die Definitionsmenge aller Exponentialfunktionen ist R. Es treten nur positve Funktionswerte auf. Alle Exponentialfunktionen der Form f(x) = ax gehen durch den Punkt (0/1). | 
|
 |
Die Graphen von f(x) = ax und g(x) = a-x = 1/ax liegen symmetrisch bezüglich der y-Achse. |
| Für 0 < a < 1 ist die Exponentialfunktion monoton fallend, für a = 1 ist die Funktion konstant, für a > 1 ist sie monoton steigend. | 
|
 |
Für 0 < a < 1 ist die positive x-Achse Asymptote. |
| Für a > 1 ist die negative x-Achse Asymptote. | 
|
 Merke:
|
