Quadratische Funktionen: Unterschied zwischen den Versionen
Aus DMUW-Wiki
| Zeile 14: | Zeile 14: | ||
|width=20px| | |width=20px| | ||
| − | |valign="top"| | + | |valign="top"| |
| + | |||
| + | <ggb_applet width="400" height="350" version="3.2" ggbBase64="UEsDBBQACAAIAFecTjwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1srVRNb9swDD2vv0LQqT0s8UecJYDdYusuBbr1kK2HHQbINm1rVSxDklNnv36UZCdugAE77CSLpKnH90imd8NekAMozWWb0XARUAJtIUve1hntTfV+Q+9ur9IaZA25YqSSas9MRuNFRK2957dX71LdyFfChAt55vCa0YoJDZToTgErdQNg3thZP3DBmTo+5b+gMPrs8Eke2q7HV4zq0Vbsy0eup+vSPdgJbj7zAy9BESGLjK4ThI5fz6AML5jI6Crwliij0YUTTbH1NlLx37I1NvycvEILIZr/BmRkbW3p0hWaQl8IXnLW2mIcDgwi5JWXpsnoZrPClMDrBrEmQeyzFVKqcnfUBvZk+AFKIpwgXqySKFrF22STfIgD/O/oXXGYWA00ggSbZLFZx8E62G6261UcrTHu7Ar8A3DYgTEomCZsAD2xVitenmi1lwf9SYqzqZO8NfesM71yYsejaWeONj+CULaSj20tYLRFqEUDxUsuh51nJ/apvx0794vDk9f3UkhFlOU9wYDxzP3pYizQU1TgYgIXMeawSU/+cBu5CHfm/nRRgrce2lh4OFUdBtMzXBNrsJRij07cCJYDSk5J33LzOF2wNV7GSkMf/7Xf5zgb8+Y4pQz/U8p0edFV6QuoFoTvnRaF7WWvycH2qJfO4Sih4Hu8esdICLNifUcA3lpCrWDC7QfL0+W8wbw/L8zpcgJhMWjEWhjcEFiPsbXYATY4PBl90LZUQZ5xPwhKSmas247KgKOv7Vrx1BBEj7tl6PC8Hm5IRoaf19EiuHHPgYA94NQZ10hV37rnTqxW9K3cpkFeW0zvetLMu8+tIum2yoU0Zw3R/Zfmw/3TNQy/puES7IgbZs6Xy/ZUVRoMGTK6xZHEaYxmzi+yhAtZUCrHH26Bzma3zdAB+Daa8JMOX3OzONP5H4rGDvL02c+5XG5xjZv79g9QSwcIjHoWOsYCAADrBQAAUEsBAhQAFAAIAAgAV5xOPIx6FjrGAgAA6wUAAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAAAAAwAAAAA=" framePossible = "true" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" /> | ||
Version vom 14. Februar 2010, 19:37 Uhr
Quadratische Funktionen
| Auf der rechten Seite ist eine andere quadratische Funktion abgebildet. Ihr Funktionsterm hat die Form x². Wie wir schon festgestellt haben, unterscheiden sich die Graphen quadratischer Funktionen stark von den Graphen linearer Funktionen.
|
|
Im rechten Bild siehst du wieder die Parabel von oben. Man kann für sie auch die Gleichung 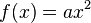 aufstellen, wobei aufstellen, wobei 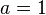 ist. In diesem Fall heißt die Funktion Normalparabel. Doch was passiert, wenn man die Zahl a verändert? ist. In diesem Fall heißt die Funktion Normalparabel. Doch was passiert, wenn man die Zahl a verändert?
Aufgabe:Verändere a mithilfe des Schiebreglers in der nebenstehenden Graphik und beobachte die Veränderung. ZUORDNUNGS-QUIZ Jetzt wird es dir nicht mehr schwer fallen, diese Sätze zu vervollständigen.
|
GEOGEBRA-APPLET
|

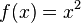 heißen Parabeln.
heißen Parabeln.
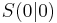 heißt Scheitel der Parabel und ist der tiefste Punkt.
heißt Scheitel der Parabel und ist der tiefste Punkt.
 Übung
Übung Zurück zur WM 2006
Zurück zur WM 2006
