Lernpfad1: Unterschied zwischen den Versionen
| Zeile 87: | Zeile 87: | ||
<div class="lueckentext-quiz"> Beispiel: 2* <math> \frac{5}{8} </math> | <div class="lueckentext-quiz"> Beispiel: 2* <math> \frac{5}{8} </math> | ||
| − | 1) Multipliziere die | + | 1) Multipliziere die natürliche Zahl mit dem '''Zähler'''. <br> |
Der '''Nenner''' bleibt stehen. <math> \frac{2*5}{8} </math> | Der '''Nenner''' bleibt stehen. <math> \frac{2*5}{8} </math> | ||
Version vom 17. März 2010, 11:06 Uhr
 Lernpfad
|
- Zeitbedarf: 35 Min.
- Material: Laufzettel und einen Stift
Viel Spaß beim Bearbeiten des Lernpfads
1.Station: Multiplikation einer natürlichen Zahl mit einem Bruch
Einführung:
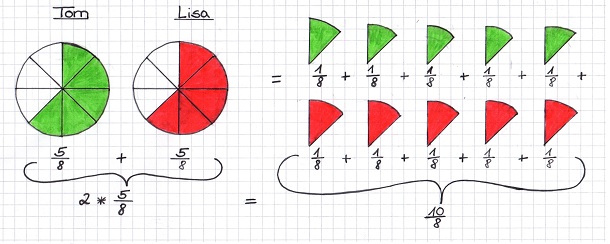
Tom und Lisa gehen zusammen Pizza essen. Ihre Pizza ist jeweils in acht Stücke aufgeteilt.
Die Pizza war so groß, dass sie beide jeweils nur 
davon essen konnten.
Wieviel Stücke Pizza haben beide zusammen gegessen?
Die Veranschaulichung durch den Schieberegler hilft dir beim Lösen der Aufgabe.
Indem du den Schieberegler über der Zahl mit der linken Maustaste nach rechts verschiebst, ändert sich die Zahl, dasselbe gilt beim Zähler. Der Nenner bleibt stets gleich.
Nun ist es deine Aufgabe, mit Hilfe des Schiebereglers die Menge Pizza zu errechnen, die beide zusammen essen
Gebe dazu in dem ersten Schieberegler die Zahl 2 ein (= Anzahl der Pizzen / Tom`s und Lisa`s Pizza) und multpliziere (= Anzahl der Stücke, die jeder der beiden gegessen hat) durch Eingabe im zweiten Schieberegler.
Gelingt dir dies, kannst du auf der rechten Seite das Ergebnis in den dargestellten Pizzen ablesen.
Welchen Bruchteil der beiden Pizzen haben die beiden zusammen gegessen?
(!
) (!) (
)
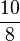Berechne nun die folgenden Aufgaben mit Hilfe des Schiebereglers.
Schreibe deine Lösungen in die Felder und klicke danach auf prüfen!.
Richtige Antworten werden mit grün angezeigt. Falsche mit rot. Bei einer falschen Lösung, probiere es noch einmal.
a)
2 * 
= 4 (Zähler) /8 (Nenner)
b)
2 * = 12 (Zähler) /8 (Nenner)
c)
2 * 
= 6 (Zähler) /8 (Nenner)
d)
2 * 
= 2 (Zähler) /8 (Nenner)
- Zur Veranschaulichung:
Beispiel von oben:
Versuche die Rechenregel für die Multiplikation einer natürlichen Zahl mit einem Bruch zu finden
Lies dir den Text genau durch und schaue dabei auf die nebenstehenden Beispiele. Ziehe die Wörte mit der linken Maustaste in die Platzhalter. Richtige Antworten bleiben stehen, falsche fallen wieder zurück. Wenn du etwas falsch eingefügt hast, probiere es nochmal.
1) Multipliziere die natürliche Zahl mit dem Zähler.
Der Nenner bleibt stehen.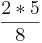 
2) Kürze das Ergebnis soweit wie möglich. =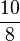 
3) Wandle in einen gemischten Bruch um. 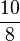= 1 *
- Zusammenfassung:
 |
Multiplikation einer natürlichen Zahl mit einem Bruch
|
| Allgemein: |
a *
 = 
|
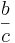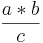
