Potenzen und Potenzfunktionen: Unterschied zwischen den Versionen
Aus DMUW-Wiki
| Zeile 9: | Zeile 9: | ||
{| | {| | ||
|- | |- | ||
| − | | <math>x^ | + | | <math>\frac{x^{n+3}}{x^{2n+6}}</math> || <math>\frac{1}{x^{n+3}}</math> |
|- | |- | ||
| − | | | + | | <math>\frac{x^{2n-3}}{x^{n+3}}</math> || <math>x^{n}\cdot \frac{1}{x^{6}}</math> |
| − | + | |- | |
| + | | <math>\frac{x^{n}}{x^{n+1}}\cdot x^{2n}</math> || <math> x^{2n-1}</math> | ||
| + | |- | ||
| + | | <math>\frac{(x+y)^{3+n}}{(x+y)^{1+n}}</math> || <math> x^{2}+2xy+y^{2}</math> | ||
| + | |- | ||
| + | | <math>\frac{(4x^{2}+8xy+4y^{2})^{n+2}}{(4x^{2}+4y^{2})^{n+2}}</math> || <math>\left( \frac{x+y}{x-y} \right) ^{n+2}</math> | ||
|} | |} | ||
</div> | </div> | ||
Version vom 21. Mai 2010, 08:14 Uhr
Potenzen
Als erstes werden Potenzen betrachtet. In der Präsentation, werden nochmal wichtige Gesetzmäßigkeiten aufgezeigt, anschließend solltest du einige Aufgaben dazu bearbeiten. {{#slideshare:potenzen-100520160702-phpapp01}}
So kannst du einige Aufgaben zu diesem Thema bearbeiten?
Hier geht es darum Terme zuzuordnen. Einige sind kompliziert, andere sind mit Hilfe der Potenzgesetze vereinfacht. Finde passende Paare.
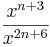 |
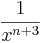
|
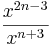 |
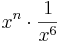
|
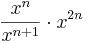 |
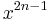
|
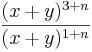 |
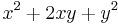
|
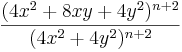 |
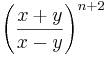
|
{{#slideshare:linear-100520104930-phpapp02}}
{{#slideshare:quadratisch-100520104946-phpapp02}}
{{#slideshare:potenzfunktion-100520132023-phpapp01}}
{{#slideshare:potenzfunktionsabbildungen-100520105117-phpapp02}}

