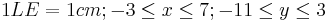|
|
| Zeile 10: |
Zeile 10: |
| | | | |
| | *Gib die Wertemenge der Funktion an. | | *Gib die Wertemenge der Funktion an. |
| | + | <popup name="Tipp"> Falls du keine Idee zur Wertemenge oder auch Definitionsmenge hast, erstelle erst die Zeichnung! |
| | + | </popup> |
| | <quiz display="simple"> | | <quiz display="simple"> |
| | {[[Bild:Peter_Fischer_Papier.png|40px]] | | {[[Bild:Peter_Fischer_Papier.png|40px]] |
| Zeile 20: |
Zeile 22: |
| | | | |
| | <div class="lueckentext-quiz"> | | <div class="lueckentext-quiz"> |
| | + | Ordne den x-Werten die passenden Funktionswerte zu! |
| | {| | | {| |
| | |x ||0,5 ||1 ||2 ||3 ||4 ||5 ||6 | | |x ||0,5 ||1 ||2 ||3 ||4 ||5 ||6 |
| Zeile 26: |
Zeile 29: |
| | |} | | |} |
| | </div> | | </div> |
| − |
| |
| | | | |
| | | | |
| Zeile 43: |
Zeile 45: |
| | | | |
| | | | |
| − | ==Aufgabe mit Funktion <math>f_(x)=x^3</math>==
| |
| − | Der Hyperbelast h ist der Graph der Funktion f mit <math>y=-x^{-3}</math> mit der Definitionsmenge <math>\mathbb{D}=\mathbb{R^+}</math>. Der Punkt <math>A_n(x/-x^{-3})</math> ist Eckpunkt von Quadraten <math>A_nB_nC_nD_n</math> mit dem Symmetriepunkt O(0/0).
| |
| − | * Fertige eine Zeichnung für x=1,5. <popup name="Tipp"> Tabellasiere f und Zeichne die Strecke [A<sub>n</sub>O] und verdopple diese...</popup>
| |
| − |
| |
| − | ''Hier ist ein Applet zur anschaulichen Darstellung[[Bild:Peter_Fischer_Applet.png|40px]]''
| |
| − | <popup name="Applet"> <ggb_applet height="600" width="1000" showMenuBar="false" showResetIcon="true" filename="Peter Fischer_Potenzfunktion_Hyperbelast.ggb" />
| |
| − | </popup>
| |
| − |
| |
| − | *Berechne den Flächeninhalt des Quadrates A<sub>2</sub>B<sub>2</sub>C<sub>2</sub>D<sub>2</sub>, wenn A<sub>2</sub> auf der Geraden g mit y= -x liegt.
| |
| − | <quiz display="simple">
| |
| − | {[[Bild:Peter_Fischer_Papier.png|40px]]
| |
| − | | type="{}" }
| |
| − | Der Flächeninhalt beträgt A<sub> A<sub>2</sub>B<sub>2</sub>C<sub>2</sub>D<sub>2</sub></sub>={ 2 _5}[FE]
| |
| − | <popup name="Lösungsschritte"> *Schnittpunkt A<sub>2</sub> zwischen y= -x und f(x) durch Gleichsetzen berechnen. Länge der Strecke <math>\overline{AO}</math> mit der Formel, Länge eines Vektors (<math>l=\sqrt{v^2_x+v^2_y}</math> berechnen. Mit Pythagoras aus der Diagonalenlänge die Kantenlänge a des Quadrates berechen. Die Fläche mit Hilfe von <math>A=a^2</math> ermitteln
| |
| − |
| |
| − | *Ermittle die nach y Aufgelöste Gleichung der Umkehrfunktion f<sup>-1</sup> zu f.
| |
| − | f<sup>-1</sup>: <math>y=\frac{1}{\sqrt[3]{-x}}</math>
| |
| − |
| |
| − | </quiz>
| |
| | | | |
| | | | |
Version vom 27. Mai 2010, 13:56 Uhr
Potenzfunktionen
{{#slideshare:potenzfunktion-100520132023-phpapp01}}
Hier eine Aufgabe, die bereits Mathematik aus verschiedenen Bereichen verbindet und Prüfungsaufgaben ähnelt.
Aufgabe mit einer Hyperbel
Gegeben ist die Funktion f ,mit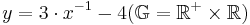
- Gib die Wertemenge der Funktion an.
- Tabellarisiere f für
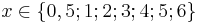 und zeichne den Graphen in ein Koordinatensystem.
und zeichne den Graphen in ein Koordinatensystem.
Für die Zeichnung: 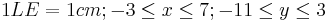
Ordne den x-Werten die passenden Funktionswerte zu!
| x |
0,5 |
1 |
2 |
3 |
4 |
5 |
6
|
| y |
2,00 |
-1,00 |
-2,50 |
-3,00 |
-3,25 |
-3,40 |
-3,50
|
Hier ist ein Applet zur anschaulichen Darstellung
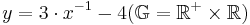
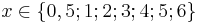 und zeichne den Graphen in ein Koordinatensystem.
und zeichne den Graphen in ein Koordinatensystem.